【CImg】霍夫变换——直线检测

霍夫变换——直线检测

考古debug，其实很久之前就解决的bug......一直忘记过来改文章....欸

=============================原文==================================　　　

此处膜拜大神（学到很多）：http://blog.csdn.net/jia20003/article/details/7724530

这个博客更了很多图像处理算法的底层实现解析，都很详细易懂，先mark

========================我是分割线=============================

霍夫变换：CV中常用的识别几何图形的方法，其中最简单的应用就是直线检测

　　　　　主要原理是对于边缘的每一个像素点（x0,y0），把可能经过它的所有直线y=kx+b，映射到k-b空间（即hough space），然后投票

　　　　　但是，对于与x轴垂直的直线，斜率不存在,无法表示，所以用参数方程表示，r = x * cos(theta) +　y * sin (theta), 其中（x,y）表示某一个边缘的像素点，r表示经过该点直线到原点的距离，theta表示r与x正轴的夹角。

　　　　　原理分析如下图：（画得..还挺chou...手残）

　　　　  

　　　　  

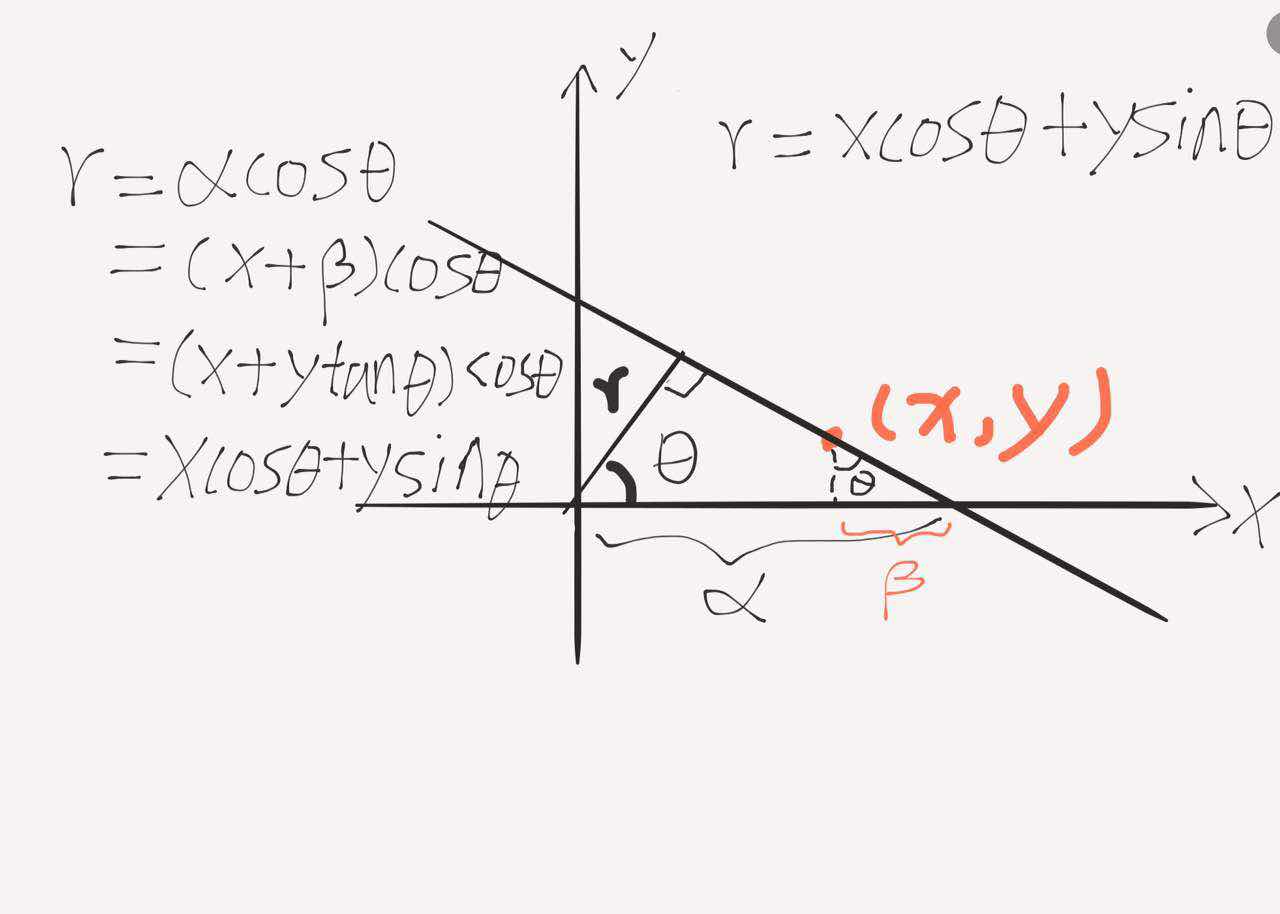
　　　　　所以最终的霍夫空间可以用r-theta表示。

　　　　　对于每个边缘点映射之后，在霍夫空间进行投票，每次有直线方程满足（r, theta）点，此处的像素值＋１：　

　　　　   　

　　　　　最后可以得到一张这样的hough-space图像：

　　　　　

　　　　　某一个点越白（像素值越大）表示，越多的点经过这条直线，这就有可能是一条边界直线

　　　　　过滤，求出局部极大值，可以得到几条直线方程（四条单像素宽直线），然后就可以根据直线方向在原图标定角点

　　　　　　　

以下为具体步骤以及实现：

　　　　　１．　彩色图像RBG->灰度图Gray

　　　　　　　　（opencv上需要注意颜色空间是RGB还是BGR，CImg中RGB分别对应0,1,2通道）

　　　　　 2.       去噪（高斯核）

　　　　　 3.       边缘提取（梯度算子、拉普拉斯算子、canny； 此处实现用sobel）

　　　　　 4.       二值化（判断此处是否为边缘点，就看灰度值==255）

　　　　     5.       映射到霍夫空间（此处准备两个容器，一个CImg用来展示hough-space概况，一个数组hough-space用来储存voting的值，因为投票过程往往有某个极大值超过255，多达几千，不能直接用灰度图来记录投票信息）

　　　　　 6.        取局部极大值，设定阈值，过滤干扰直线

　　　　　 7.        绘制直线、标定角点

实现：

　　　　1. 转灰度

　　　　　　可以用自带API，或者自己写

　　　　2. 高斯去噪（采用了一个标准差为1的高斯核）

　　　　　　

　　　　3. sobel算子提取边界

　　　　　sobel时梯度算子的一种

　　　　　

　　　　4. 二值化（应该设置一个阈值，对不同的图，不同的阈值，以便完整显示边界）

　　　　　在高斯去噪和边界提取之后都需要二值化

　　　　　以下时同一张图片的二值化（阈值分别为60、80、100、127），可见，保持较好的边缘信息需要合适的阈值

   

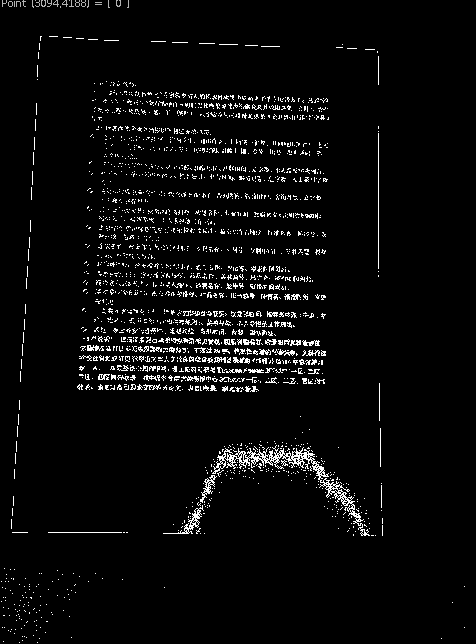
　　　　5. 映射到霍夫空间

　　　　　先在原图构造一个x-y平面，一一对应各点的直线方程计算O（0,0）为事实上的原点，O‘（width/2，height/2）为构造平面的原点

　　　　　然后构造一个hough-space，其中纵轴表示theta的刻度，theta取值0～PI，分成500个刻度，r的最大值为max_length=sqrt((width/2)^2 + (height/2)^2),又r存在正负值，故而hough-space的横轴需要2*max_length

       

　　　　　　

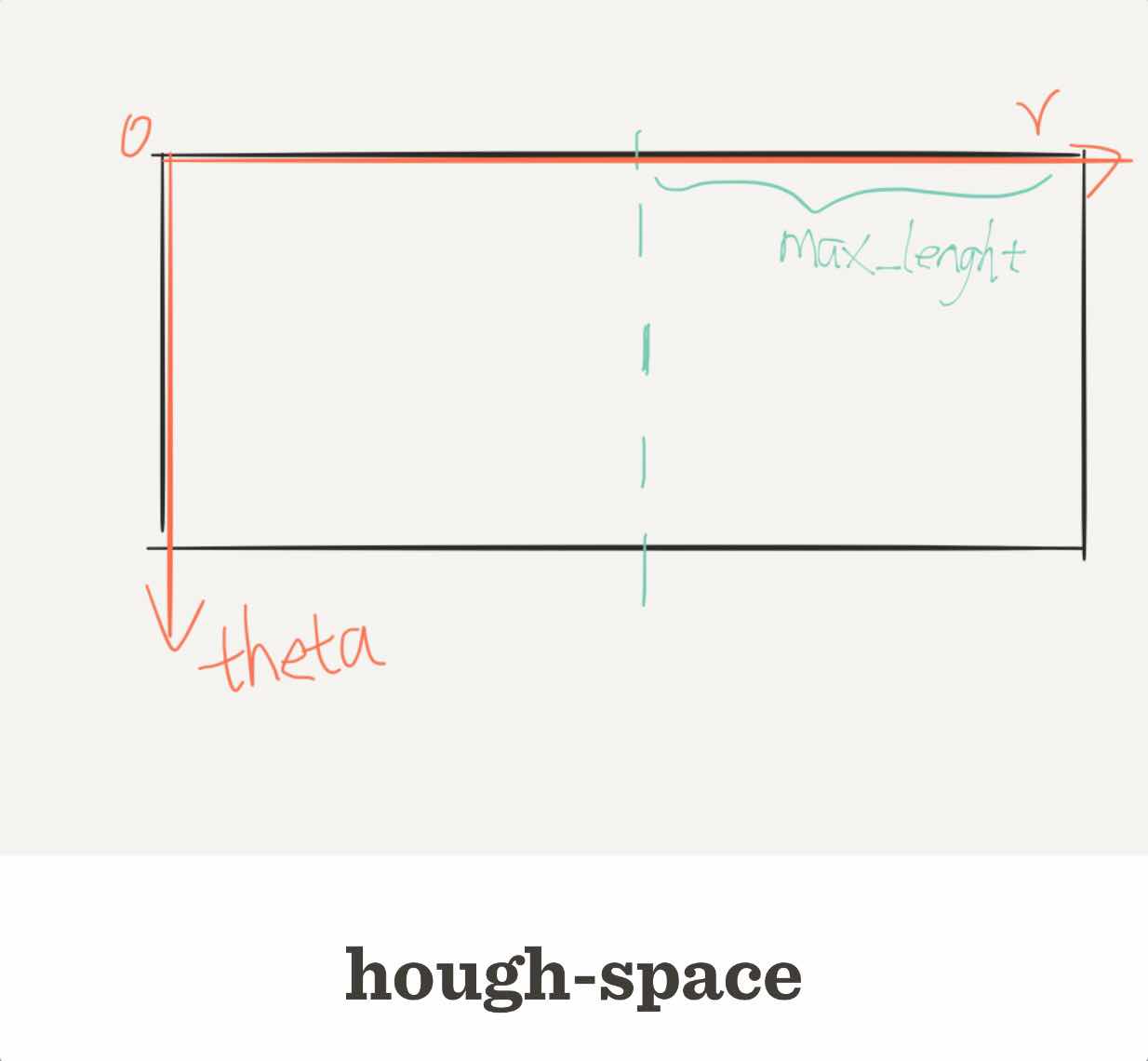
    //霍夫空间,图像初始化
    CImg<unsigned char> output( * max_length, hough_space, , );
    int** hough = new int*[];
    for (int k = ; k < hough_space; k ++)
        hough[k] = new int[*max_length] ();
    output.fill();

    //检测每一个点的所有可能直线方程，并记录投票，以及最大值
    int max_hough = ;
    for (int x = ; x < width; x ++) {
        for (int y = ; y < height; y ++) {
            int temp = (int)inputImage.atXYZC(x, y, , );
            if (temp == )continue;
            else {
                for (int degree = ; degree < hough_space; degree ++) {
                    double r = (x - centerX) * cos(degree * hough_intervals) + (y - centerY) * sin(degree * hough_intervals);
                    r += max_length;
                    if (r <  || (r >=  * max_length))continue;
                    unsigned char temp = output.atXYZC((unsigned int)r, degree, , ) + ;
                    output.atXYZC((unsigned int)r, degree, , ) = temp;
                    hough[degree][(int)r] ++;
                    if (max_hough < hough[degree][(int)r])max_hough = hough[degree][(int)r];
                }
            }
        }
    }
    cout << "max_hough = " << max_hough << endl;    

　　　　　6. 取局部极大值，设定阈值，过滤干扰直线（直线方程存储在lines中）

//输出直线轨迹
    CImg<unsigned char> output1(width, height, , );
    output1.fill();

    //设置阈值
    int threshold = int(max_hough * value);
    cout << "threshold = " << threshold << endl;
    int count = ;
    vector<pair<int, int> > lines;
    //遍历hough空间，找到所有比阈值大的点
    for (int row = ; row < hough_space; row ++) {
        for (int col = ; col <  * max_length; col ++) {
            bool newLines = true;
            int temp = hough[row][col];
            if (hough[row][col] > threshold) {
                for (int k = ; k < lines.size(); k ++) {
                    //判断极值
                    if ((abs(lines[k].first - row) <  || abs(( - lines[k].first) + row) < ) && abs(lines[k].second - col) < ) {
                        if (hough[row][col] > hough[lines[k].first][lines[k].second]) {
                            lines[k].first = row;
                            lines[k].second = col;
                        }
                        newLines = false;
                    }
                }
                if (newLines) {
                    lines.push_back(make_pair(row, col));
                    //cout << "push " << row << " "<< col << endl;
                }
            }
        }
    }

　　　　　7. 绘制直线、标定角点（角点信息存储在node中）

　　　　　　因为有的直线斜率K可能不存在，所以我判断两条直线相较的条件是在draw lines的时候，看一下某像素点是不是已经被标记直线，若是，则说明有直线与当前直线相交，记录交点（但是这种方法不是很好，最后讨论优缺点）

 //角点
     vector<pair<int, int> > node;

     //draw lines
     for (int k = ; k < lines.size(); k ++) {
         int row = lines[k].first;
         int col = lines[k].second;
         //cout << "line " << k << " = " << row << " " << col << endl;
         double dy = sin(row * hough_intervals);
         double dx = cos(row * hough_intervals);
         if ((row <= hough_space /  ) || (row >=  * hough_space / )) {
             for (int sRow = ; sRow < height; ++sRow) {
                 int sCol;
                 if (row ==  || row == )sCol =  (int)(col - max_length) + centerX;
                 sCol = (int)((col - max_length - ((sRow - centerY) * dy)) / dx) + centerX;
                 if (sCol < width && sCol >= ) {
                     if((int)output1.atXYZC(sCol, sRow, , ) == )node.push_back(make_pair(sCol, sRow));
                     else output1.atXYZC(sCol, sRow, , ) = (unsigned char);
                 }
             }
         }
         else {
             for (int sCol= ; sCol < width; ++sCol) {
                 int sRow;
                 if(row == )sRow = (int)(col - max_length) + centerY;
                 sRow = (int)((col - max_length - ((sCol - centerX) * dx)) / dy) + centerY;
                 if (sRow < height && sRow >= ) {
                     if((int)output1.atXYZC(sCol, sRow, , ) == )node.push_back(make_pair(sCol, sRow));
                     else output1.atXYZC(sCol, sRow, , ) = (unsigned char);
                 }
             }
         }
     }

     //在原图上标记
     CImg<unsigned char> output2(scrImage);

     //标记
     for (int k = ; k < lines.size(); k ++) {
         unsigned int w = output2.width();
         unsigned int h = output2.height();

         int range = ;

         cout << "node x = " << node[k].first << " " << "   y = " << node[k].second << endl;

         for (int c = -range; c < range; c ++) {
             for (int r = -range; r < range; r ++) {
                 int distance = (int)sqrt(c * c + r * r + 0.0);
                 if (node[k].first>= range && node[k].first < width - range && node[k].second >= range && node[k].second < height - range) {
                     if (distance <=  && node[k].first + c >=  && node[k].first + c < width && node[k].second + r >=  && node[k].second + r < height) {
                         output2.atXYZC(node[k].first + c, node[k].second + r, , ) = (unsigned char)();
                         output2.atXYZC(node[k].first + c, node[k].second + r, , ) = (unsigned char)();
                         output2.atXYZC(node[k].first + c, node[k].second + r, , ) = (unsigned char)();
                     }
                 }
             }
         }
     }

分析：

　　　几幅图像的实验结果如下：

　　　去噪、提取边缘、二值化之后（图1\2\3\4）

   

　　　依次为图1\2\3\4的霍夫空间表示

　　　　　

　　　

　　　

　　   

　　　分别为图1\2\3\4的边界直线绘制，可知四张图的边界都可以检测到

   

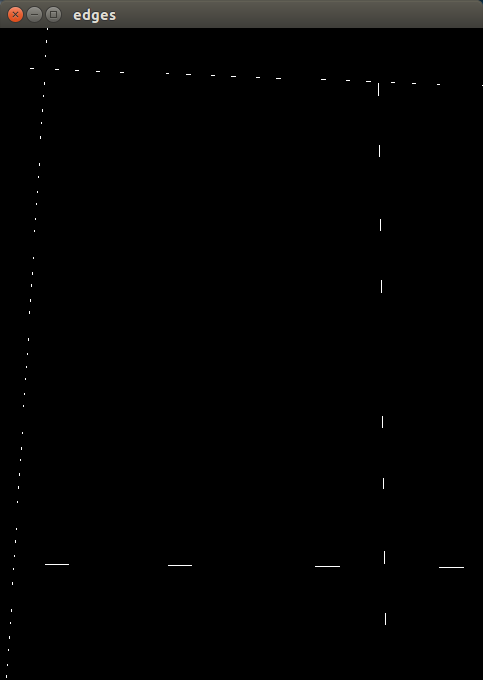
　　　在原图上标定交点

   

　　　可以发现，四张图中，只有图2的角点没有标好，其余三张图的边界直线都有斜率K不存在的情况，所以，我的标定方法适用，当直线的斜率存在时，就很可能出现一下情况：（红蓝分别表示两条直线的像素点，可以看到虽然它们相交，但是在像素表示上并无交点，这时候需要多加一个判断，是否需要用直线方程y=kx+b来直接求出交点）