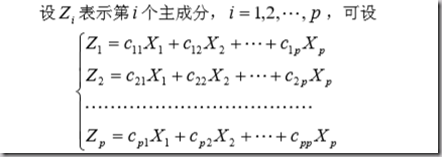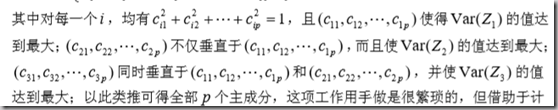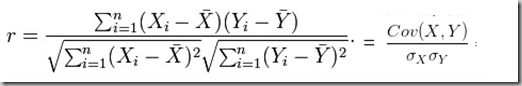【数学建模】day10-主成分分析

0.

关于主成分分析的详细理解以及理论推导，这篇blog中讲的很清楚。

主成分分析是一种常用手段。这应该与因子分析等区别开来，重点在于理解主成分分析的作用以及什么情况下使用主成分分析，本文重点讲解如何使用PCA。

1.

主成分分析是一种降维方法。

实际上这个降维是这样做的：原始变量有m维，PCA主成分变量有t维（t<m），那么就相当于把这m维分别往t维上投影。

例如我们要做回归分析，如果自变量众多，彼此之间又具有复杂的相关性，那么我们考虑对自变量个数进行“减少”。而这个减少不能够丢失有效信息，由此可以使用主成分分析。

主成分分析的主要思想是，对原始众多自变量进行【线性组合】（这其实是向PCA方向投影的过程），从而得到新的PCA变量(个数通常比原始变量少)。对于每一个新变量，其线性组合的系数向量叫该主成分的方向（重点在于如何得到这个PCA方向）；不同主成分的方向是正交的，从而保证新的变量彼此不相关，消除了糅合性。

具体来说，是：

原始变量Xi(i = 1,2,…p)，主成分变量Z(z = 1,2…p)，则：

其中，要求满足：

注意：

　　1）主成分分析的结果受量纲的影响，由于各变量的单位可能不一样，如果各自改 变量纲，结果会不一样，这是主成分分析的大问题，回归分析是不存在这种情况的， 所以实际中可以先把各变量的数据标准化，然后使用协方差矩阵或相关系数矩阵进行分析。（相关系数就是标准化变量的协方差）

　　2）使方差达到大的主成分分析不用转轴（由于统计软件常把主成分分析和因子 分析放在一起，后者往往需要转轴，使用时应注意）。

　　3）主成分的保留。用相关系数矩阵求主成分时，Kaiser主张将特征值小于1的主成 分予以放弃（这也是SPSS软件的默认值）。

　　4）在实际研究中，由于主成分的目的是为了降维，减少变量的个数，故一般选取 少量的主成分（不超过5或6个），只要它们能解释变异的70％～80％（称累积贡献率） 就行了。

2.

如何选取主成分？

或者说：重点在于找到主成分方向，因为有了PCA方向，把原始变量向PCA方向上投影就得新的PCA变量。

明确目的在于线性组合原始变量得到：

（z是向量）

在系数平方和为1下，使得z的方差最大。（这样就使得新的变量z1，z2…差异最大，就代表我们抓住了原始变量的大多数信息）；同时，保证各个主成分变量的系数矩阵c两两正交（这代表我们使得新的变量彼此不糅合，不相关）。

简单推导：

设原始变量数据：

（X称作设计阵）每列代表一个变量指标，每行是一组数据。

首先将X标准化。

设新变量z = c1x1 + c2x2 +… + cpxp；

系数向量C = (c1,c2,…cp).T

系数向量C就是主成分的方向。

目的在于使得原始变量X的每一行，在C的方向投影后，在C的方向上达到方差最大。也就是：

　　Z = CX （Z是X向C投影）

　　max E（(Z-E(Z))‘* (Z-E(Z))）

这个求max可以经过变化，转换^{【具体看推导blog，仅仅使用PCA可以略过】}为求max E((X - E(x))' * (X - E(X)))

由于X标准化了（归一化过），E(X) = 0;

从而变为 max E（X.T*X）

而X.T * X 是一个二次型的。

那么，最大值就在：这个矩阵X.T * X 的最大特征值λ对应的特征向量c = [c1,c2...cp]处取得。

c还要经过单位化处理。

也就是说，这就得到了第一主成分的方向c；把X向c上投影得到了第一主成分Z1.

而这个半正定矩阵X.T *X的不同特征向量是正交的，从而把第二特征向量作为第二主成分的方向。

以此类推。

这里，X标准化后，X.T*X / (n-1)实际上是原始变量x1,x2…xp的相关系数矩阵。（协方差矩阵）

求解时，实际上是计算这个相关系数矩阵。

3.

PCA步骤：

　　1. 列出设计阵X，将X标准化处理。

　　2. 求相关系数矩阵R（标准化后，这也就是协方差矩阵）。这里要知道，这个R可以用：

X.T*X / (n-1)求得。也可以使用MATLAB求相关系数矩阵命令。

　　3. 求R的特征值（从大到小排列），以及对应的单位标准正交特征向量。

　　3. 从特征值大到小选择PCA变量：先选取最大的特征值以及其特征向量，从而构成第一个主成分变量，这个特征向量就是PCA方向。计算累计贡献率：已选取的特征值之和占所有特征值之和的比重。

　　4. 重复步骤3，直到累计贡献率达标或者选取了足够的PCA变量。

　　5. 单纯考虑累积贡献率有时是不够的，还需要考虑选择的主成分对原始变量的贡献 值，我们用相关系数的平方和来表示.如果选取的主成分为 z1,z2,…zr ，则它们对原 变量 xi 的贡献值为:

　　　　　　　　　　pi = ∑ (r(zj,xi))^2；（注1）

　　　　　（即每一个主成分变量与xi的相关系数平方的和。）

　　6. 进而我们可以用主成分变量对问题做出其他分析（如回归分析等）。

注1：两个向量的相关系数就是两向量夹角的余弦，展开来说就是：

4.

一个例子：

 

5.

MATLAB实现

函数使用：

1. 求矩阵X列向量间的相关系数矩阵：

r = corrcoef(X)

param:

　　X：这个矩阵X的每一列看做一个向量

return：

　　r： 相关系数矩阵。返回每两列之间的相关系数组成的矩阵，对称阵，对角为方差，一个向量的方差就是对向量的每个数求var。

　　注意使用时不必对设计阵做标准化处理。因为我们实际要求的是标准化变量的协方差矩阵，而就是原设计阵的相关系数矩阵。

2. matlab做PCA分析

[vec1,lamda,rate] = pcacov(r)

param：

　　r：原始数据的相关系数矩阵

return：

　　vec1: r的特征向量

　　lamda: 对应的特征值

　　rate: 各个主成分的贡献率

3. 累计求和函数cumsum

y = cumsum(x,axis)

对x矩阵累计求和

param:

　　axis：轴，axis = 1则对列向量累计求和

　　axis = 2则对行向量累计求和

return:

　　y: 累和矩阵

4. 标准化化处理函数

y = zccore(x)

param:

　　x： 矩阵或者向量，标准化处理，若是矩阵，是对列向量标准化处理

return:

　　y： 处理后的矩阵或者向量

5. 主成分分析做线性回归最小二乘估计函数

[c,s,t] = princomp(x)

param:

　　x是设计阵

return:

　　c:  对主成分变量做多元线性回归分析，回归方程的系数

　　s:  这个是做主成分分析得到的特征向量矩阵，每一列是一个特征向量（单位化）

　　t：相应的特征值

应用主成分分析+回归分析案例:

分别做主成分回归以及原始变量直接回归。

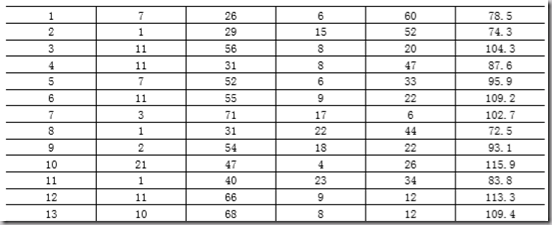
数据保存：

data.txt

    78.5
     74.3
     104.3
     87.6
     95.9
     109.2
     102.7
     72.5
     93.1
     115.9
     83.8
     113.3
     109.4 

matlab求解如下：

（注：也可以直接用princomp函数，更简单，下面使用标准的pcacov函数）

 clc,clear
  load data.txt %导入数据
 [m,n] = size(data);
  x0 = data(:,[:n-]);
  y0 = data(:,n);
  hg1 = [ones(m,),x0] \ y0; %普通多元线性回归系数.列向量
 hg1 = hg1' %显示
 fprintf('y = % f',hg1());
  for i = :n
      if hg1(i) >
          fprintf('+ % f*x% d',hg1(i),i-);
      else
          fprintf('% f*x% d',hg1(i),i-);
      end
  end

 fprintf('\n');
  r = corrcoef(x0) %相关系数矩阵
 xd = zscore(x0);
  yd = zscore(y0); %标准化处理
 [vec1,lamda,rate] = pcacov(r) %PCA
  f = repmat(sign(sum(vec1)),size(vec1,),);
 %产生与vec1同维数的元素为+/-1的矩阵
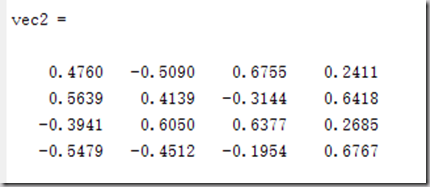
 vec2 = vec1.*f %修改特征值正负号，使得特征值的所有分量和为+
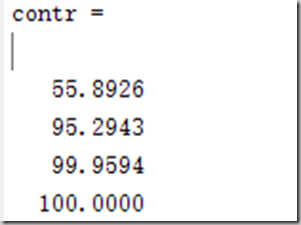
 contr = cumsum(rate) %计算累计贡献率
 df = xd * vec2; %计算所有主成分的得分
 num = input('请输入主成分个数：')
 hg21 = df(:,[:num]) \ yd %主成分变量回归系数
 hg22 = vec2(:,:num) * hg21 %标准化变量的回归系数
 hg23 = [mean(y0) - std(y0)*mean(x0)./std(x0)*hg22,std(y0)*hg22'./std(x0)]
  % 转换，求原始变量的回归方程系数

 fprintf('y = % f',hg23());
  for i = :n
      if hg23(i) >
          fprintf('+ % f*x% d',hg23(i),i-);
      else
          fprintf('% f*x% d',hg23(i),i-);
      end
  end
  fprintf('\n')
  %下面计算两种回归分析的剩余标准差
 rmse1=sqrt(sum((x0*hg1(:end)'+hg1(1)-y0).^2)/(m-n))
  rmse2=sqrt(sum((x0*hg23(:end)'+hg23(1)-y0).^2)/(m-num)) 

结果如下：

相关系数矩阵：

PCA分析得到的：特征值、特征向量、贡献率等结果：

做代码所示处理后的特征向量：

累计贡献率：

可以看到，最后一个变量几乎没有贡献，使用前三个PCA成分得到:（其实两个也可以）

其中，hg21是主成分变量回归系数、hg22是标准化X的回归系数(没有常数项)，hg23是原始X的回归系数（第一个是常数项）

从而，PCA后的结果为：

而在原始变量上直接做回归分析的结果为：

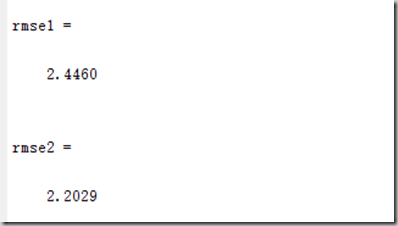
代码中还计算了两个剩余标准差：

可见，PCA后再回归的剩余标准差要小，效果更好，这也证明了使用PCA是有效的。