UOJ#422 小Z的礼物

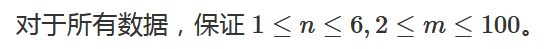
非常神奇的一个套路......首先min-max容斥一波，变成枚举子集然后求所有子集min的期望。

一个子集的期望怎么求？我们可以求出所有的r = 2nm - n - m个选法中能够选到这个子集的方案数k，那么概率就是k / r，则期望是r / k。

发现子集数量上天了......但是这个方案数k十分之小。

于是我们非常神奇的转换思路。

求出对于每个k，有多少个子集满足恰有k种选法能够选到。

这样我们就能够把k当成一维状态，进行状压DP。压轮廓线上的点是否选入子集，一格一格转移。

每种选法在右边/下边的格子统计。每次枚举当前这格选不选，然后观察方案数是否增加。

如果选了一个格子，集合数量改变，要乘一个-1作为系数。

 #include <bits/stdc++.h>

 typedef long long LL;
 const int N = , MO = ;

 int G[N][N], n, m, f[][][], inv[];
 char str[N];

 inline void add(int &a, const int &b) {
     a = a + b;
     while(a >= MO) a -= MO;
     while(a < ) a += MO;
     return;
 }

 inline void out(int x) {
     for(int i = ; i < m; i++) printf("%d", (x >> i) & );
     return;
 }

 int main() {

     scanf("%d%d", &n, &m);
     for(int i = ; i <= n; i++) {
         scanf("%s", str + );
         for(int j = ; j <= m; j++) {
             G[j][i] = (str[j] == '*');
         }
     }
     std::swap(n, m);

     /// input over

     int lm = ( << m), up =  * n * m - n - m;
     f[][][] = -;
     for(int i = ; i <= n; i++) {
         for(int j = ; j < m; j++) {
             /// pos (i, j)
             int p = (i - ) * m + j;

             for(int w = ; w <= up; w++) {
                 for(int s = ; s < lm; s++) {
                     f[(p + ) & ][w][s] = ;
                 }
             }

             for(int w = ; w <= up; w++) {
                 for(int s = ; s < lm; s++) {
                     if(!f[p & ][w][s]) continue;
                     //printf("f (%d %d) w=%d ", i, j, w); out(s); printf(" = %d \n", f[p][w][s]);
                     int c = f[p & ][w][s], temp = ;
                     if(j) temp += (s >> (j - )) & ;
                     if(i > ) temp += (s >> j) & ;
                     add(f[(p + ) & ][w + temp][s & (~( << j))], c); /// not choose
                     if(G[i][j + ]) {
                         add(f[(p + ) & ][w + (i > ) + (j > )][s | ( << j)], -c); /// choose
                     }
                 }
             }
         }
     }
     //printf("\n");
     inv[] = inv[] = ;
     for(int i = ; i <= up; i++) {
         inv[i] = 1ll * inv[MO % i] * (MO - MO / i) % MO;
     }
     int ans = , p = n * m;
     for(int w = ; w <= up; w++) {
         for(int s = ; s < lm; s++) {
             add(ans, 1ll * f[p & ][w][s] * inv[w] % MO * up % MO);
             //printf("ed : w=%d ", w); out(s); printf(" = %d \n", f[p][w][s]);
         }
     }
     printf("%d\n", ans);
     return ;
 }

AC代码

[update]注意到这个DP数组中的那个s维，一定是“*”的子集。否则不会转移，为0，没有意义。

not choose那个转移表示当前不是*或者不选，当前这里覆盖上面那个*或左边那个*。

choose表示这里是*且加入集合，有两种摆法覆盖它，同时多了一个*导致要乘一个-1。