HDU1028 （整数拆分）

Ignatius and the Princess III

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 16191    Accepted Submission(s): 11407

Problem Description

"Well, it seems the first problem is too easy. I will let you know how foolish you are later." feng5166 says.

"The second problem is, given an positive integer N, we define an equation like this:
  N=a[1]+a[2]+a[3]+...+a[m];
  a[i]>0,1<=m<=N;
My question is how many different equations you can find for a given N.
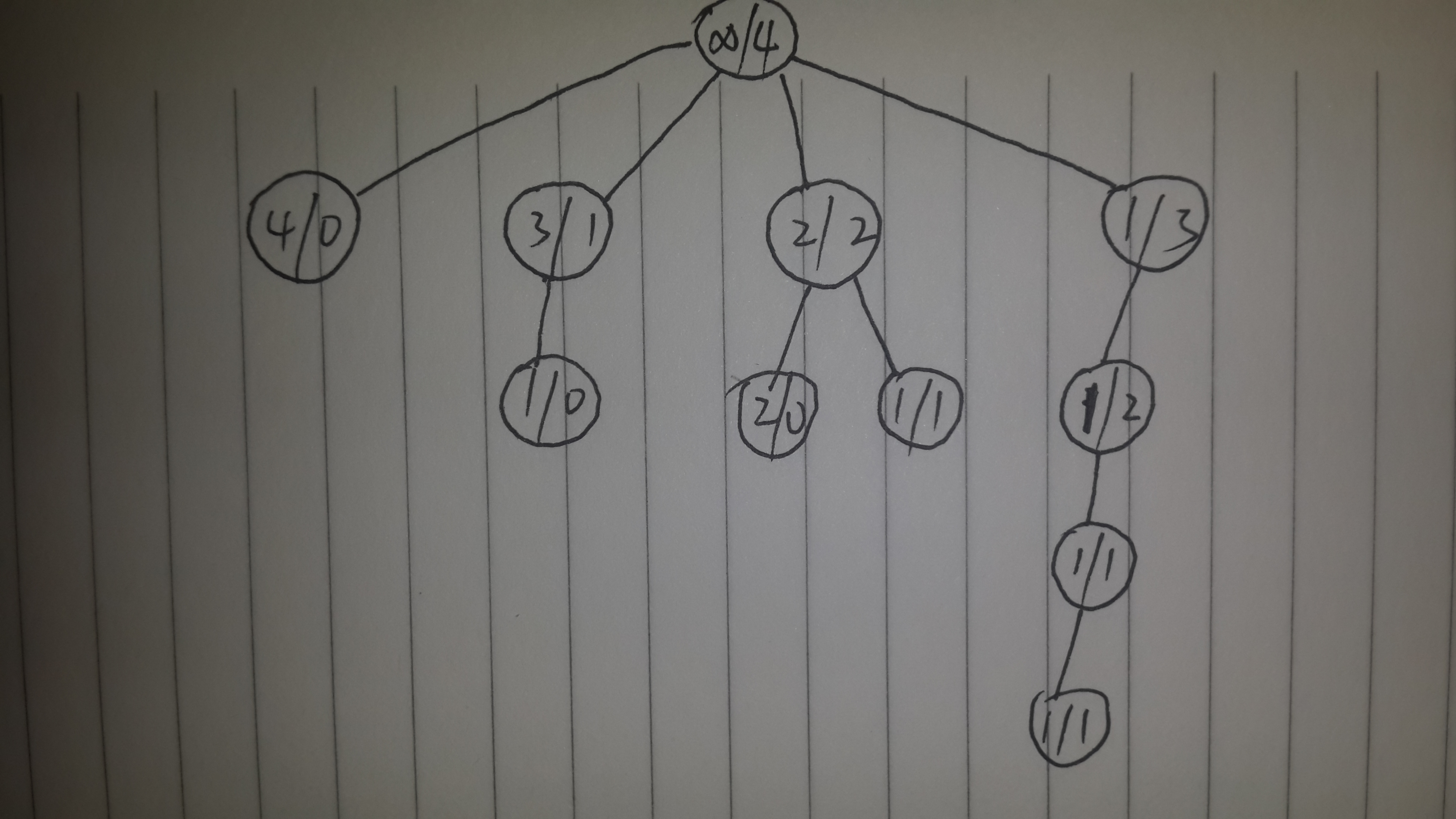
For example, assume N is 4, we can find:
  4 = 4;
  4 = 3 + 1;
  4 = 2 + 2;
  4 = 2 + 1 + 1;
  4 = 1 + 1 + 1 + 1;
so the result is 5 when N is 4. Note that "4 = 3 + 1" and "4 = 1 + 3" is the same in this problem. Now, you do it!"

 

Input

The input contains several test cases. Each test case contains a positive integer N(1<=N<=120) which is mentioned above. The input is terminated by the end of file.

 

Output

For each test case, you have to output a line contains an integer P which indicate the different equations you have found.

 

Sample Input

4

10

20

 

Sample Output

5

42

627

 

Author

Ignatius.L

 

整数拆分问题

试着用数形结合的思想理解dfs

每个节点维护两个值，当前结点的值和剩下可传递给儿子的值，为了避免重复，所以每个节点的值都大于等于儿子节点的值

 

如果每次询问都来一遍dfs会进行很多重复运算，所以可用记忆化搜索

 

/*
ID: LinKArftc
PROG: 1028.cpp
LANG: C++
*/

#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <string>
#include <utility>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define eps 1e-8
#define randin srand((unsigned int)time(NULL))
#define input freopen("input.txt","r",stdin)
#define debug(s) cout << "s = " << s << endl;
#define outstars cout << "*************" << endl;
const double PI = acos(-1.0);
const double e = exp(1.0);
const int inf = 0x3f3f3f3f;
const int INF = 0x7fffffff;
typedef long long ll;

const int maxn = ;
int dp[maxn][maxn];

int dfs(int last, int res) {
    if (res <= ) return ;
    if (dp[last][res]) return dp[last][res];
    int ret = ;
    if (last >= res) {
        for (int i = res; i >= ; i --) {
            ret += dfs(i, res - i);
        }
    } else {
        for (int i = last; i >= ; i --) {
            ret += dfs(i, res - i);
        }
    }
    dp[last][res] = ret;
    return ret;
}

int main() {
    int n;
    while (~scanf("%d", &n)) {
        int ans = ;
        memset(dp, , sizeof(dp));
        for (int i = n; i >= ; i --) ans += dfs(i, n - i);
        printf("%d\n", ans);
    }

    return ;
}