[BJOI2019]勘破神机

[BJOI2019]勘破神机

推式子好题

m=2，斐波那契数列，$f_{n+1}$项

不妨$++l,++r$，直接求$f_n$

求$\sum C(f_n,k)$，下降幂转化成阶乘幂，这样都是多项式了，方便交换求和号

最后面的斐波那契数列用通项公式求。二项式展开。

交换求和号之后，枚举i,j 最后一项是等比数列求和。

%rqy

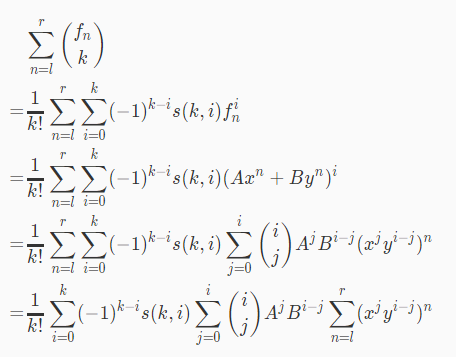
m=3，

n为奇数是0

n是偶数时，令n=n/2 递推公式：$g_n=4\times g_{n-1}+g_{n-2}$

证明：枚举从后往前第一个完全分出的块，除了块长为2的方案额外多一个外，其它都是两种。$g_n=g_{n-1}+2\times \sum_{i=0}^{n-1} g_{i}$

再写出：$g_{n-1}=g_{n-2}+2\times \sum_{i=0}^{n-2} g_{i}$两式做差移项即可得到。

用特征方程可以解得$g_n$的通项公式

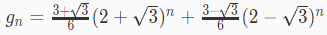
$\sqrt 5$在mod 998244353下不存在，可以用$a+b\sqrt5$形式表示

注意，等比数列求和：$1+Q+....+Q^n=\frac{1-Q^{n+1}}{1-Q}$注意是n+1，因为有n+1项

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}

namespace Miracle{
const int mod=;
const int N=;
int C;
int ad(int x,int y){
    return x+y>=mod?x+y-mod:x+y;
}
int mul(int x,int y){
    return (ll)x*y%mod;
}
ll qm(ll x,ll y){
    ll ret=;
    while(y){
        if(y&) ret=mul(ret,x);
        x=mul(x,x);
        y>>=;
    }
    return ret;
}
int inv[+];
int ni(int x){
    // cout<<" ni x "<<x<<endl;
    return x<=?inv[x]:qm(x,mod-);
}
struct po{
    int a,b;
    po(){
        a=;b=;
    }
    po(int aa,int bb){
        a=aa;b=bb;
    }
    po friend operator +(po a,po b){
        return po(ad(a.a,b.a),ad(a.b,b.b));
    }
    po friend operator -(po a,po b){
        return po(ad(a.a,mod-b.a),ad(a.b,mod-b.b));
    }
    po friend operator ~(po a){
        int mom=ni(ad(mul(a.a,a.a),mod-mul(C,mul(a.b,a.b))));
        // cout<<" mom "<<mom<<endl;
        return po(mul(a.a,mom),ad(,mod-mul(a.b,mom)));
    }
    po friend operator -(po a){
        return po(ad(,mod-a.a),ad(,mod-a.b));
    }
    po friend operator *(po a,po b){
        return po(ad(mul(a.a,b.a),mul(mul(a.b,b.b),C)),ad(mul(a.a,b.b),mul(a.b,b.a)));
    }
    po friend operator *(po a,int c){
        return po(mul(a.a,c),mul(a.b,c));
    }
    po friend operator /(po a,po b){
        return a*(~b);
    }
    void op(){
        cout<<" a "<<a<<" b "<<b<<endl;
    }
}A,B,X,Y,mi[N][];
po qm(po x,ll y){
    po ret;ret.a=;
    while(y){
        if(y&) ret=ret*x;
        x=x*x;
        y>>=;
    }
    return ret;
}
po calc(po Q,ll n){
    // Q.op();
    if(Q.a==&&Q.b==){
        return po((n+)%mod,);
    }
    po tmp=Q;tmp=qm(tmp,n+);
    tmp=-tmp;tmp.a=ad(tmp.a,);
    Q=-Q;Q.a=ad(Q.a,);
    // Q.op();
    // Q=~Q;
    // Q.op();
    return tmp*(~Q);
}
int s[N][N],c[N][N];
int main(){
    int t;rd(t);int m;rd(m);
    inv[]=;
    for(reg i=;i<=;++i){
        inv[i]=mul(mod-mod/i,inv[mod%i]);
    }
    if(m==) {
        C=;A=po(,ni());B=po(,mod-ni());
        X=po(ni(),ni());Y=po(ni(),mod-ni());
    }
    else {
        C=;A=po(ni(),ni());B=po(ni(),mod-ni());
        X=po(,);Y=po(,mod-);
    }
    mi[][]=mi[][]=mi[][]=mi[][]=po(,);
    for(reg i=;i<=;++i){
        mi[i][]=mi[i-][]*A;
        mi[i][]=mi[i-][]*B;
        mi[i][]=mi[i-][]*X;
        mi[i][]=mi[i-][]*Y;
    }

    s[][]=;
    for(reg i=;i<=;++i){
        for(reg j=;j<=;++j){
            s[i][j]=ad(mul(s[i-][j],i-),s[i-][j-]);
        }
    }
    c[][]=;
    for(reg i=;i<=;++i){
        c[i][]=;
        for(reg j=;j<=;++j){
            c[i][j]=ad(c[i-][j-],c[i-][j]);
        }
    }

    ll l,r,k;
    while(t--){
        rd(l);rd(r);rd(k);
        if(m==) {
            ++l,++r;
            po ans;
            for(reg i=;i<=k;++i){
                // cout<<" i "<<i<<endl;
                po tmp;
                for(reg j=;j<=i;++j){
                    // cout<<" jj "<<j<<endl;
                    tmp=tmp+mi[j][]*mi[i-j][]*(calc(mi[j][]*mi[i-j][],r)-calc(mi[j][]*mi[i-j][],l-))*c[i][j];
                    // cout<<" bac "<<endl;
                }
                if((k-i)&) tmp=-tmp;
                ans=ans+(tmp*s[k][i]);
            }
            for(reg i=;i<=k;++i) ans=ans*inv[i];
            ans=ans*qm((r-l+)%mod,mod-);

            printf("%d\n",ans.a);
        }
        else{
            ll L=l,R=r;
            l=(l+)/,r=r/;
            po ans;
            for(reg i=;i<=k;++i){
                // cout<<" i "<<i<<endl;
                po tmp;
                for(reg j=;j<=i;++j){
                    // cout<<" jj "<<j<<endl;
                    tmp=tmp+mi[j][]*mi[i-j][]*(calc(mi[j][]*mi[i-j][],r)-calc(mi[j][]*mi[i-j][],l-))*c[i][j];
                    // cout<<" bac "<<endl;
                }
                if((k-i)&) tmp=-tmp;
                ans=ans+(tmp*s[k][i]);
            }
            for(reg i=;i<=k;++i) ans=ans*inv[i];
            ans=ans*qm((R-L+)%mod,mod-);

            // ans.op();
            printf("%d\n",ans.a);
        }
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/