Jacobi并行拆解【补充】
作者:桂。
时间:2018-04-24 22:04:52
链接:http://www.cnblogs.com/xingshansi/p/8934373.html
前言
本文为Jacobi并行拆解一文的补充,给出另一种矩阵运算的思路。
一、算法流程
对于复数相关矩阵R,通过矩阵变换,在维度不变的情况下,转化为实数矩阵:

对于MUSIC算法,该思路可以降低Jacobi运算复杂度。额外的操作仅仅是少量的乘法操作,即耗费少量硬件资源换取更快速的处理时间。
直接复数转实数,需要将nxn的矩阵扩展为2n x 2n的矩阵,而直接转化的相关矩阵仍然为 n x n,降低了Jacobi的复杂度。
容易证明U*Un为新的特征向量,而U可与导向矢量a提前乘法处理,存储到Ram里。
这里可以看出:(R + J*conj(R)*J)/2等价于中心对称线阵的前、后项空间平滑算法,而斜Hermitian矩阵的特征向量与转化的特征向量等价,因此可以得出特性:对于具备中心对称特性的线阵,复数->实数,既可以降低Jacobi复杂度,又具备了解相干信号的能力。
二、仿真验证
未做实数化处理,code:
clc;clear all;close all
%Ref:Narrowband direction of arrival estimation for antenna arrays
doas=[-30 -5 40]*pi/180; %DOA's of signals in rad.
P=[1 1 1]; %Power of incoming signals
N=10; %Number of array elements
K=1024; %Number of data snapshots
d=0.5; %Distance between elements in wavelengths
noise_var=1; %Variance of noise
r=length(doas); %Total number of signals
% Steering vector matrix. Columns will contain the steering vectors
% of the r signals
A=exp(-i*2*pi*d*(0:N-1)'*sin([doas(:).']));
% Signal and noise generation
sig=round(rand(r,K))*2-1; % Generate random BPSK symbols for each of the
% r signals
noise=sqrt(noise_var/2)*(randn(N,K)+i*randn(N,K)); %Uncorrelated noise
X=A*diag(sqrt(P))*sig+noise; %Generate data matrix
R=X*X'/K; %Spatial covariance matrix
[Q ,D]= svd(R); %Compute eigendecomposition of covariance matrix
[D,I]=sort(diag(D),1,'descend'); %Find r largest eigenvalues
Q=Q(:,I);%Sort?the?eigenvectors?to?put?signal?eigenvectors?first
Qs=Q (:,1:r); %Get the signal eigenvectors
Qn=Q(:,r+1:N); %Get the noise eigenvectors
% MUSIC algorithm
%?Define?angles?at?which?MUSIC???spectrum????will?be?computed
angles=(-90:0.1:90);
%Compute steering vectors corresponding values in angles
a1=exp(-i*2*pi*d*(0:N-1)'*sin([angles(:).']*pi/180));
for k=1:length(angles)%Compute?MUSIC???spectrum??
music_spectrum(k)= 1/(a1(:,k)'*Qn*Qn'*a1(:,k));
end
figure(1)
plot(angles,abs(music_spectrum))
title('MUSIC Spectrum')
xlabel('Angle in degrees')
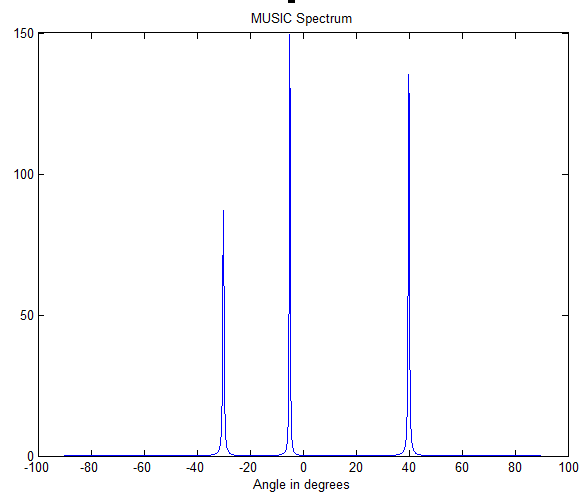
实数化处理,code:
clc;clear all;close all
%Ref:Narrowband direction of arrival estimation for antenna arrays
doas=[-30 -5 40]*pi/180; %DOA's of signals in rad.
P=[1 1 1]; %Power of incoming signals
N=10; %Number of array elements
K=1024; %Number of data snapshots
d=0.5; %Distance between elements in wavelengths
noise_var=1; %Variance of noise
r=length(doas); %Total number of signals
% Steering vector matrix. Columns will contain the steering vectors
% of the r signals
A=exp(-i*2*pi*d*(0:N-1)'*sin([doas(:).']));
% Signal and noise generation
sig=round(rand(r,K))*2-1; % Generate random BPSK symbols for each of the
% r signals
noise=sqrt(noise_var/2)*(randn(N,K)+i*randn(N,K)); %Uncorrelated noise
X=A*diag(sqrt(P))*sig+noise; %Generate data matrix
R=X*X'/K; %Spatial covariance matrix
%% Reconstruct
%实数
n = size(R);
I = eye(n/2);
J = fliplr(eye(n));
U = 1/sqrt(2)*[I fliplr(I);1j*fliplr(I) -1j*I];
R = 0.5*U*(R+J*conj(R)*J)*U';
% Reconstruct_end
[Q ,D]= svd(R); %Compute eigendecomposition of covariance matrix
[D,I]=sort(diag(D),1,'descend'); %Find r largest eigenvalues
Q=Q(:,I);%Sort?the?eigenvectors?to?put?signal?eigenvectors?first
Qs=Q (:,1:r); %Get the signal eigenvectors
Qn=Q(:,r+1:N); %Get the noise eigenvectors
% MUSIC algorithm
%?Define?angles?at?which?MUSIC???spectrum????will?be?computed
angles=(-90:0.1:90);
%Compute steering vectors corresponding values in angles
a1=exp(-i*2*pi*d*(0:N-1)'*sin([angles(:).']*pi/180));
for k=1:length(angles)%Compute?MUSIC???spectrum??
music_spectrum(k)= 1/(a1(:,k)'*U'*Qn*Qn'*U*a1(:,k));
end
figure(1)
plot(angles,abs(music_spectrum))
title('MUSIC Spectrum')
xlabel('Angle in degrees')
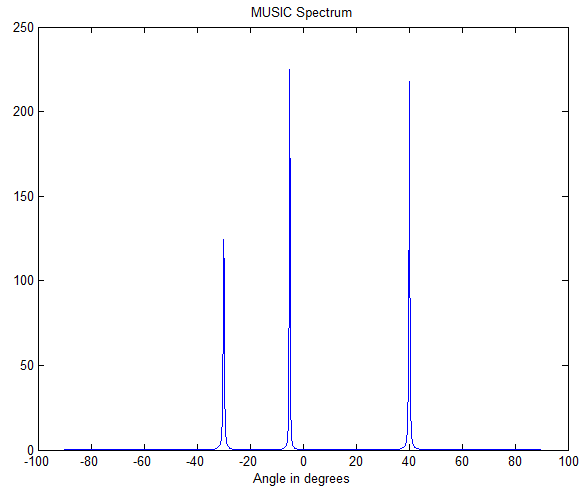
Jacobi并行拆解【补充】的更多相关文章
- Jacobi并行拆解
作者:桂. 时间:2018-04-23 21:12:02 链接:http://www.cnblogs.com/xingshansi/p/8921815.html 前言 本文主要是复数矩阵分解的拆解思 ...
- 进程队列补充、socket实现服务器并发、线程完结
目录 1.队列补充 2.关于python并发与并行的补充 3.TCP服务端实现并发 4.GIL全局解释器锁 什么是保证线程安全呢? GIL与Lock 5.验证多线程的作用 对结论的验证: 6.死锁现象 ...
- 深入理解Java虚拟机之JVM垃圾回收随笔
1.对象已经死亡? 1.1引用计数法:给对象中添加一个引用计数器,每当有一个地方引用他时,计数器值就加1:当引用失效时,计数器值就减1:任何时刻计数器都为0的对象就是不可能再被使用 的.但是它很难解决 ...
- 《OpenCL异构并行编程实战》补充笔记散点,第一至四章
▶ 总体印象:适合 OpenCL 入门的书,有丰富的代码和说明,例子较为简单.先把 OpenCL 代码的基本结构(平台 → 设备 → 上下文 → 命令队列 → 创建缓冲区 → 读写缓冲区 → 编译代码 ...
- Python基础补充(二) 多核CPU上python多线程并行的一个假象【转】
在python上开启多个线程,由于GIL的存在,每个单独线程都会在竞争到GIL后才运行,这样就干预OS内部的进程(线程)调度,结果在多核CPU上: python的多线程实际是串行执行的,并不会同一时间 ...
- 《OpenCL异构并行编程实战》补充笔记散点,第五至十二章
▶ 第五章,OpenCL 的并发与执行模型 ● 内存对象与上下文相关而不是与设备相关.设备在不同设备之间的移动如下,如果 kernel 在第二个设备上运行,那么在第一个设备上产生的任何数据结果在第二个 ...
- OpenMP 《并行程序设计导论》的补充代码
▶ 使用 OpenMP 和队列数据结构,在各线程之间传递信息 ● 代码,使用 critical 子句和 atomic 指令来进行读写保护 // queue.h #ifndef _QUEUE_H_ #d ...
- Pthreads 《并行程序设计导论》的补充代码
▶ 关于单链表的访问,插入结点和删除结点操作,并且将其推广到多线程中去. ● 代码,通用的随机数生成 // my_rand.h #ifndef _MY_RAND_H_ #define _MY_RAND ...
- .Net并行编程(一)-TPL之数据并行
前言 许多个人计算机和工作站都有多个CPU核心,可以同时执行多个线程.利用硬件的特性,使用并行化代码以在多个处理器之间分配工作. 应用场景 文件批量上传 并行上传单个文件.也可以把一个文件拆成几段分开 ...
随机推荐
- 配置Git绑定Git@OSC
用户名,这个名字会出现在以后的提交记录中. git config --global user.name "Git@OSC用户名" 然后是Email,同样,这个Email也会出现在你 ...
- Atlas系列一:Atlas功能特点FAQ
1:Atlas是否支持多字符集? 支持,可以在test.cnf中指定. #默认字符集,设置该项后客户端不再需要执行SET NAMES语句charset = utf8 2:Atlas是否支持事物操作? ...
- Linux驱动程序:统计单词个数
本例为Android升读探索(卷1):HAL与驱动开发 一书中附带的演示样例程序.现粘贴出来,以便查阅. 终端操作,可能用到的命令: insmond word_count.ko lsmod | gre ...
- join联表查询方法
$model = Shipping::join('shipping_area', 'shipping_area.shipping_id', '=', 'shipping.shipping_id') - ...
- leetcode笔记:Bulls and Cows
一. 题目描写叙述 You are playing the following Bulls and Cows game with your friend: You write down a numbe ...
- 单目视觉里程计 mono vo
之前为了修改svo进行了一些不同的尝试,两个视频demo在以下. 效果1 视频链接: https://v.qq.com/x/page/d0383rpx3ap.html 在不同数据集上測试 效果2 视频 ...
- Android开发之使用Handler刷新UI控件
一.为什么必须使用Handler 线程安全问题 这个问题要理解的话很容易,如果没有这个约束,那么同时有两个线程对一个UI控件进行调整,那么控件自然就没法正常的工作,而为了解决这种二义性(就是一个东西同 ...
- IF函数
语法:IF(logical_test,value_if_true,value_if_false) logical_test:表示计算结果为 TRUE 或 FALSE 的任意值或表达式 value_if ...
- 转 安装php时报gd相关的错误(gd_ctx.c)
在安装php时,报如下错误 In file included from /kk/php-5.4.0/ext/gd/gd.c:103: /kk/php-5.4.0/ext/gd/gd_ctx.c: In ...
- Android短信管家视频播放器代码备份
自己保留备份,增强记忆 这是video的类 public class VideoActivity extends Activity { /** * 解析网络页面 */ private WebVie ...
