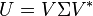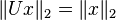正交矩阵、正规矩阵和酉矩阵(转自Ramble Over The Cloud~)
网址:http://blog.csdn.net/alec1987/article/details/7414450
在数学中,正规矩阵 是与自己的共轭转置交换的复系数方块矩阵,也就是说, 满足
其中 是 的共轭转置。
如果 是实系数矩阵,那么条件简化为 其中 是 的转置矩阵。
矩阵的正规性是检验矩阵是否可对角化的一个简便方法:任意正规矩阵都可在经过一个酉变换后变为对角矩阵,反过来所有可在经过一个酉变换后变为对角矩阵的矩阵都是正规矩阵。
在复系数矩阵中,所有的酉矩阵、埃尔米特矩阵和斜埃尔米特矩阵都是正规的。同理,在实系数矩阵中,所有的正交矩阵、对称矩阵和斜对称矩阵都是正规的。两个正规矩阵的乘积也不一定是正规矩阵
酉矩阵
n阶复方阵U的n个列向量是U空间的一个标准正交基,则U是酉矩阵(Unitary Matrix)。
一个简单的充分必要判别准则是:
方阵U的共扼转置乘以U等于单位阵,则U是酉矩阵。即酉矩阵的逆矩阵与其伴随矩阵相等。
酉方阵在量子力学中有着重要的应用。酉等价是标准正交基到标准正交基的特殊基变换。
其中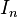 为n阶单位矩阵,
为n阶单位矩阵, 为U的共轭转置,则称其为幺正矩阵或酉矩阵。即,矩阵U为幺正矩阵,当且仅当其共轭转置
为U的共轭转置,则称其为幺正矩阵或酉矩阵。即,矩阵U为幺正矩阵,当且仅当其共轭转置 为其逆矩阵:
为其逆矩阵:
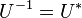 。
。
若幺正矩阵的元素都是实数,其即为正交矩阵。与正交阵G不会改变两个实向量的内积类似,
幺正矩阵U不改变两个复向量的内积:
在数学中,正规矩阵  是与自己的共轭转置交换的复系数方块矩阵,也就是说,
是与自己的共轭转置交换的复系数方块矩阵,也就是说, 满足
满足
其中 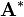 是
是  的共轭转置。
的共轭转置。
如果 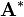 是实系数矩阵,那么条件简化为
是实系数矩阵,那么条件简化为 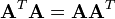 其中
其中  是
是  的转置矩阵。
的转置矩阵。
矩阵的正规性是检验矩阵是否可对角化的一个简便方法:任意正规矩阵都可在经过一个酉变换后变为对角矩阵,反过来所有可在经过一个酉变换后变为对角矩阵的矩阵都是正规矩阵。
在复系数矩阵中,所有的酉矩阵、埃尔米特矩阵和斜埃尔米特矩阵都是正规的。同理,在实系数矩阵中,所有的正交矩阵、对称矩阵和斜对称矩阵都是正规的。两个正规矩阵的乘积也不一定是正规矩阵
酉矩阵
n阶复方阵U的n个列向量是U空间的一个标准正交基,则U是酉矩阵(Unitary Matrix)。
一个简单的充分必要判别准则是:
方阵U的共扼转置乘以U等于单位阵,则U是酉矩阵。即酉矩阵的逆矩阵与其伴随矩阵相等。
酉方阵在量子力学中有着重要的应用。酉等价是标准正交基到标准正交基的特殊基变换。
|
其中
若酉矩阵的元素都是实数,其即为正交矩阵。与正交矩阵G不会改变两个实向量的内积类似, 幺正矩阵U不改变两个复向量的内积: 若 酉矩阵的特征值都是绝对值为1的复数,即分布在复平面的单位圆上,因此酉矩阵行列式的值也为1。 其中V是酉矩阵,Σ是主对角线上元素绝对值为1的对角阵。 对任意 n,所有n阶酉矩阵的集合关于矩阵乘法构成一个群。 性质
|
正交变换最初来自于维基百科,这种矩阵元被称为简正坐标.用质量加权坐标表示的分子内部运动的动能,用质量加权坐标表示的分子内部势能,用质量加权坐标表示的分子内部势能,由力常数的数学表达式可以知道fij = fji因而矩阵为一个正交变换通过酉变换可以把矩阵变形成为对角矩阵的形式:。则有:它的每一个矩阵元都是分子所有质量加权坐标的线性组合,总的矩阵元的数量恰巧等于质量加权坐标的个数,这些矩阵元就被称作简正坐标,而这些变换中分子的势能不变,所以正交变换又称为酉变换.
矩阵定义和相关符号
以下是一个 4 × 3 矩阵:
某矩阵 A 的第 i 行第 j 列,或 i,j位,通常记为 A[i,j] 或 Ai,j。在上述例子中 A[2,3]=7。
在C语言中,亦以 A[j] 表达。(值得注意的是,与一般矩阵的算法不同,在C中,"行"和"列"都是从0开始算起的)
此外 A = (aij),意为 A[i,j] = aij 对于所有 i 及 j,常见于数学著作中。
一般环上构作的矩阵
给出一环 R,M(m,n, R) 是所有由 R 中元素排成的 m× n 矩阵的集合。若 m=n,则通常记以 M(n,R)。这些矩阵可加可乘 (请看下面),故 M(n,R) 本身是一个环,而此环与左 R 模 Rn 的自同态环同构。
若 R 可置换,则 M(n, R) 为一带单位元的 R-代数。其上可以莱布尼茨公式定义行列式:一个矩阵可逆当且仅当其行列式在 R 内可逆。
在百度百科内,除特别指出,一个矩阵多是实数矩阵或虚数矩阵。
分块矩阵
分块矩阵是指一个大矩阵分割成“矩阵的矩阵”。举例,以下的矩阵
可分割成 4 个 2×2 的矩阵。
此法可用于简化运算,简化数学证明,以及一些电脑应用如VLSI芯片设计等。
特殊矩阵类别
对称矩阵是相对其主对角线(由左上至右下)对称, 即是 ai,j=aj,i。
埃尔米特矩阵(或自共轭矩阵)是相对其主对角线以复共轭方式对称, 即是 ai,j=a*j,i。
特普利茨矩阵在任意对角线上所有元素相对, 是 ai,j=ai+1,j+1。
随机矩阵所有列都是概率向量, 用于马尔可夫链。
矩阵运算 给出 m×n 矩阵 A 和 B,可定义它们的和 A + B 为一 m×n 矩阵,等 i,j 项为 (A + B)[i, j] = A[i, j] + B[i, j]。举例:
另类加法可见于矩阵加法.
若给出一矩阵 A 及一数字 c,可定义标量积 cA,其中 (cA)[i, j] = cA[i, j]。 例如
这两种运算令 M(m, n, R) 成为一实数线性空间,维数是mn.
若一矩阵的列数与另一矩阵的行数相等,则可定义这两个矩阵的乘积。如 A 是 m×n 矩阵和 B 是 n×p矩阵,它们是乘积 AB 是一个 m×p 矩阵,其中
(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + ... + A[i, n] * B[n, j] 对所有 i 及 j。
例如
此乘法有如下性质:
(AB)C = A(BC) 对所有 k×m 矩阵 A, m×n 矩阵 B 及 n×p 矩阵 C ("结合律").
(A + B)C = AC + BC 对所有 m×n 矩阵 A 及 B 和 n×k 矩阵 C ("分配律")。
C(A + B) = CA + CB 对所有 m×n 矩阵 A 及 B 和 k×m 矩阵 C ("分配律")。
要注意的是:可置换性不一定成立,即有矩阵 A 及 B 使得 AB ≠ BA。
对其他特殊乘法,见矩阵乘法。
六、其他性质
线性变换,转置。
矩阵是线性变换的便利表达法,皆因矩阵乘法与及线性变换的合成有以下的连系:
以 Rn 表示 n×1 矩阵(即长度为n的矢量)。对每个线性变换 f : Rn -> Rm 都存在唯一 m×n 矩阵 A 使得 f(x) = Ax 对所有 x ∈ Rn。 这矩阵 A "代表了" 线性变换 f。 今另有 k×m 矩阵 B 代表线性变换 g : Rm -> Rk,则矩阵积 BA 代表了线性变换 g o f。
矩阵 A 代表的线性代数的映像的维数称为 A 的矩阵秩。矩阵秩亦是 A 的行(或列)生成空间的维数。
m×n矩阵 A 的转置是由行列交换角式生成的 n×m 矩阵 Atr (亦纪作 AT 或 tA),即 Atr[i, j] = A[j, i] 对所有 i and j。若 A 代表某一线性变换则 Atr 表示其对偶算子。转置有以下特性:
(A + B)tr = Atr + Btr,(AB)tr = BtrAtr。
注记
矩阵可看成二阶张量,因此张量可以认为是矩阵和向量的一种自然推广。
七、矩阵卡
矩阵卡是由深圳网域提出的一种保护个人帐号的系统,它是由一张表格组成,横排是A\B\C\D等英文字母,在竖排是1.2.3等阿拉伯数字,在登录时必须通过矩阵卡的验证才可以进入游戏..。现广泛应用于各游戏公司和银行等的账号保密防盗。
正交矩阵、正规矩阵和酉矩阵(转自Ramble Over The Cloud~)的更多相关文章
- 对称矩阵、Hermite矩阵、正交矩阵、酉矩阵、奇异矩阵、正规矩阵、幂等矩阵
2016-01-27 21:03 524人阅读 评论(0) 收藏 举报 分类: 理论/笔记(20) 版权声明:本文为博主原创文章,转载请注明出处,谢谢! 题目:对称矩阵.Hermite矩阵.正交矩阵. ...
- 矩阵的基本性质 之 对称矩阵,Hermite矩阵,正交矩阵,酉矩阵
1.对称矩阵 2.Hermite矩阵 3.正交矩阵 4.酉矩阵
- Stage3D学习笔记(四):正交矩阵
我们上一章节显示图片的时候,会发现我们制定的顶点在Stage3D中其实是存在一个区间的: x轴(从左到右):[-1.0-1.0] y轴(从下到上):[-1.0-1.0] z轴(从近到远):[0-1.0 ...
- 【线性代数】标准正交矩阵与Gram-Schmidt正交化
1.标准正交矩阵 假设矩阵Q有列向量q1,q2,...,qn表示,且其列向量满足下式: 则 若Q为方阵,由上面的式子则有 我们举例说明上述概念: 2.标准正交矩阵的好处 上面我们介绍了标准正交 ...
- 正交矩阵、EVD、SVD
原文地址:https://www.jianshu.com/p/1004dd342fe2 一.正交矩阵 二.EVD 特征值分解(Eigen Value Decomposition, EVD). 对于对称 ...
- Opengl正交矩阵 glOrthof 数学原理(转)
http://blog.sina.com.cn/s/blog_6084f588010192ug.html 在opengles1.1中设置正交矩阵只要一个函数调用就可以了:glOrthof,但是open ...
- 线性代数之——正交矩阵和 Gram-Schmidt 正交化
这部分我们有两个目标.一是了解正交性是怎么让 \(\hat x\) .\(p\) .\(P\) 的计算变得简单的,这种情况下,\(A^TA\) 将会是一个对角矩阵.二是学会怎么从原始向量中构建出正交向 ...
- 酉矩阵(unitary matrix)
复方阵 U 称为酉矩阵,如果满足: U∗U=UU∗=I 换句话说,矩阵 U 的共轭转置 U∗ 就是 U 的逆矩阵. U∗=U−1 1. unitary matrix 保持内积不变 ⟨Ux,Uy⟩=⟨x ...
- 证明2x2正交矩阵专置后还是正交矩阵
[ x1 x2 y1 y2] x1^2+y1^2=1 x2^2 + y2^2=1 x1*x2 + y1*y2=0 如果专置后还是 x1^2 + x2^2=1 y1^2 +y2^2=1 x1* ...
随机推荐
- hdu6446 Tree and Permutation 2018ccpc网络赛 思维+dfs
题目传送门 题目描述:给出一颗树,每条边都有权值,然后列出一个n的全排列,对于所有的全排列,比如1 2 3 4这样一个排列,要算出1到2的树上距离加2到3的树上距离加3到4的树上距离,这个和就是一个排 ...
- Codeforces Round #305 (Div. 2) A
Description While Mike was walking in the subway, all the stuff in his back-bag dropped on the groun ...
- c#缓存帮助类
public static class CacheHelper { static object _lockObj = new object(); private static Dictionary&l ...
- Java RESTful框架的性能比较
https://colobu.com/2015/11/17/Jax-RS-Performance-Comparison/
- JavaScript trim 实现去除字符串首尾指定字符的简单方法
String.prototype.trim = function (char, type) { if (char) { if (type == 'left') { return this.replac ...
- ECharts基本设置
theme = { // 全图默认背景 // backgroundColor: ‘rgba(0,0,0,0)’, // 默认色板 color: ['#ff7f50','#87cefa','#da70d ...
- java生成复杂word文档
在Web应用中,有时需要按照固定的模板将数据导出到Word,如流程审批单,在流程处理完成后将处理过程按照流程单的要求导出,有时程序中需要实现生成 标准Word文档,要求能够打印,并且保持页面样式不变, ...
- 如何获取Android手机的唯一标识
有很多场景和需求你需要用到手机设备的唯一标识符. 在Android中,有以下几种方法获取这样的ID. 1. The IMEI: 仅仅只对Android手机有效: 1 2 TelephonyManage ...
- 转:POST 400 Bad Request The request sent by the client was syntactically incorrect
最近在做Web开发的时候,使用$.post提交数据,但是回调函数却没有被触发,按F12看控制台输出是:POST *** 400 Bad Request 后台是SpringMVC的,设置了断点也不会被触 ...
- pat1066. Root of AVL Tree (25)
1066. Root of AVL Tree (25) 时间限制 100 ms 内存限制 65536 kB 代码长度限制 16000 B 判题程序 Standard 作者 CHEN, Yue An A ...


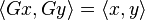

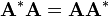
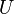 为n阶方阵,则下列条件等价:
为n阶方阵,则下列条件等价: