Arnold变换（猫脸变换）

Arnold变换是Arnold在遍历理论研究中提出的一种变换。由于Arnold本人最初对一张猫的图片进行了此种变换,因此它又被称为猫脸变换。Arnold变换可以对图像进行置乱,使得原本有意义的图像变成一张无意义的图像。经典Arnold变换是一个二维可逆映射，但离散形式的Arnold变换具有周期性随着图像大小的变化而变化。

定义1 称整数到自身的变换

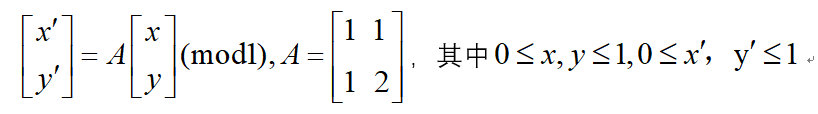
，其中为二维Arnold变换。

定义2  称整数到自身的变换，其中

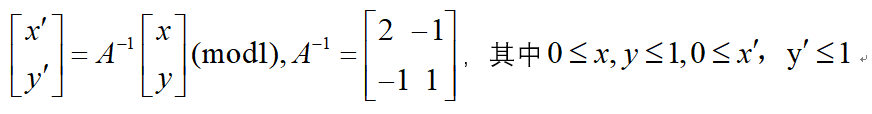
为二维Arnold逆变换。

设为图像上的点，在Arnold变换下变成点，因此，使用Arnold变换可以实现图像位置的变换。但是当时，Arnold变换不适合的图像。

对经典Arnold变换的矩阵A进行替换，可以得到广义Arnold变换。