Kruskal-Wallis test

python机器学习-乳腺癌细胞挖掘（博主亲自录制视频）https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

项目联系QQ：231469242

https://github.com/thomas-haslwanter/statsintro_python/tree/master/ISP/Code_Quantlets/08_TestsMeanValues/kruskalWallis

# -*- coding: utf-8 -*-
import numpy as np
# additional packages
from scipy.stats.mstats import kruskalwallis
'''
 .. currentmodule:: scipy.stats.mstats
    This module contains a large number of statistical functions that can
    be used with masked arrays.
    Most of these functions are similar to those in scipy.stats but might
    have small differences in the API or in the algorithm used. Since this
    is a relatively new package, some API changes are still possible.
'''
# Get the data
'''
#These data could be a comparison of the smog levels in four different cities.
city1 = np.array([68, 93, 123, 83, 108, 122])
city2 = np.array([119, 116, 101, 103, 113, 84])
city3 = np.array([70, 68, 54, 73, 81, 68])
city4 = np.array([61, 54, 59, 67, 59, 70])
'''

group1=[27,2,4,18,7,9]
group2=[20,8,14,36,21,22]
group3=[34,31,3,23,30,6]
list_groups=[group1,group2,group3]

def Kruskawallis_test(list_groups):
    # Perform the Kruskal-Wallis test,返回True表示有显著差异，返回False表示无显著差异
    print"Use kruskawallis test:"
    h, p = kruskalwallis(list_groups)
    print"H value:",h
    print"p",p

    # Print the results
    if p<0.05:
        print('There is a significant difference between the cities.')
        return True
    else:
        print('No significant difference between the cities.')
        return False

Kruskawallis_test(list_groups)    

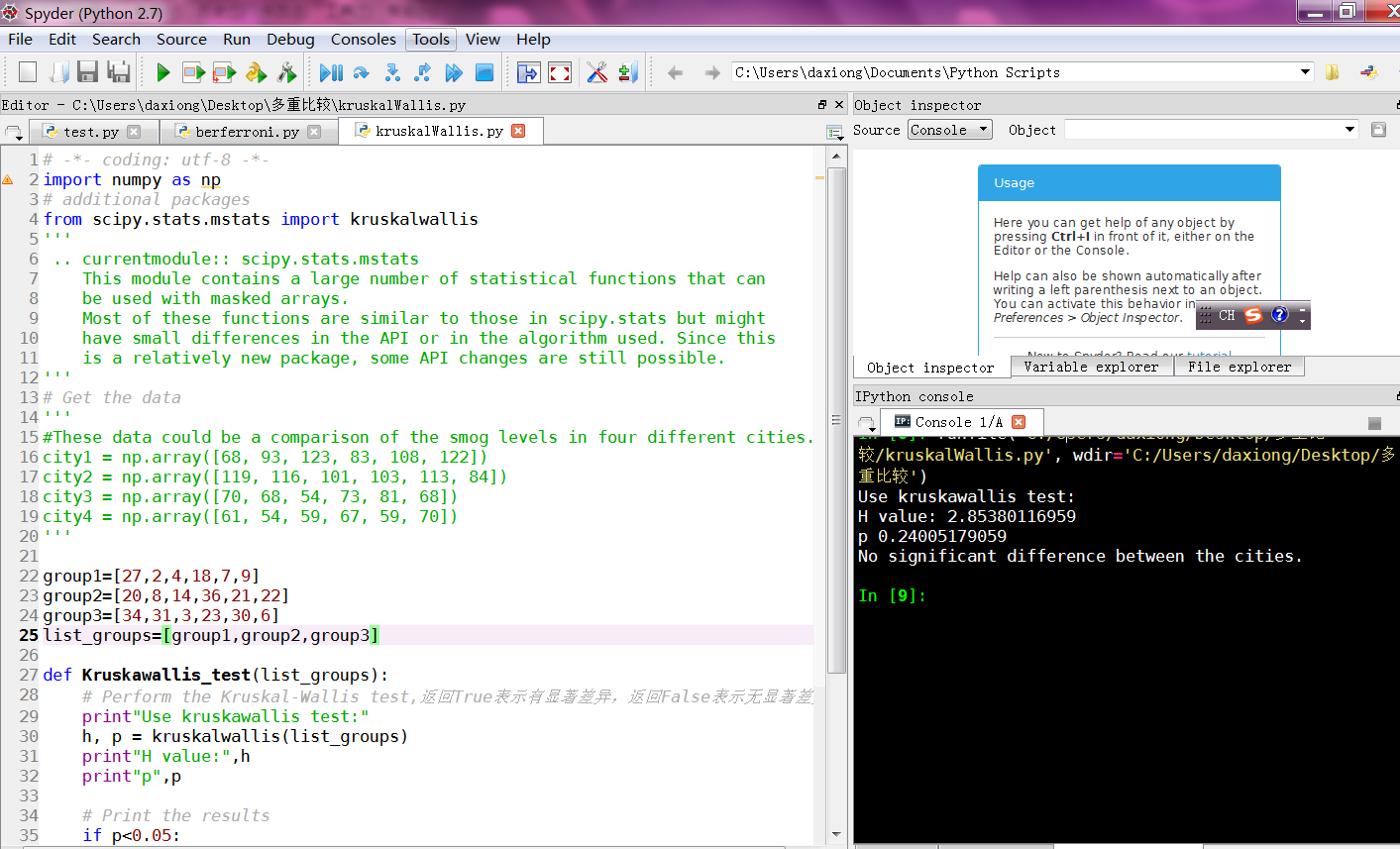
当样本数据非正态分布，两组数对比时用mann-whitney检验，三组或更多时用kruskal-wallis检验

kruskal-wallis 是一个独立单因素方差检验的版本

kruskal-wallis能用于排序计算

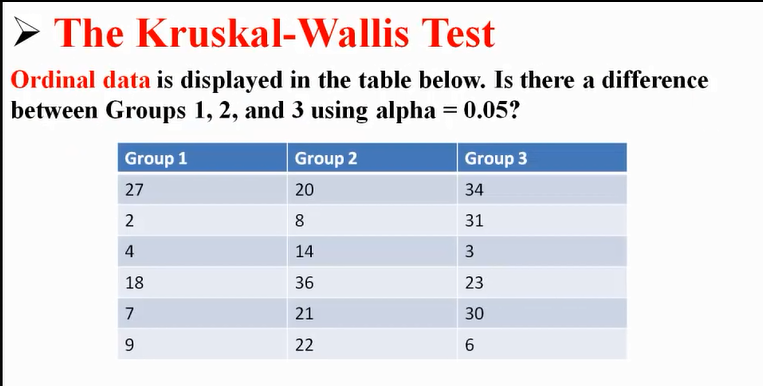
样本数据

流程

H0和H1假设

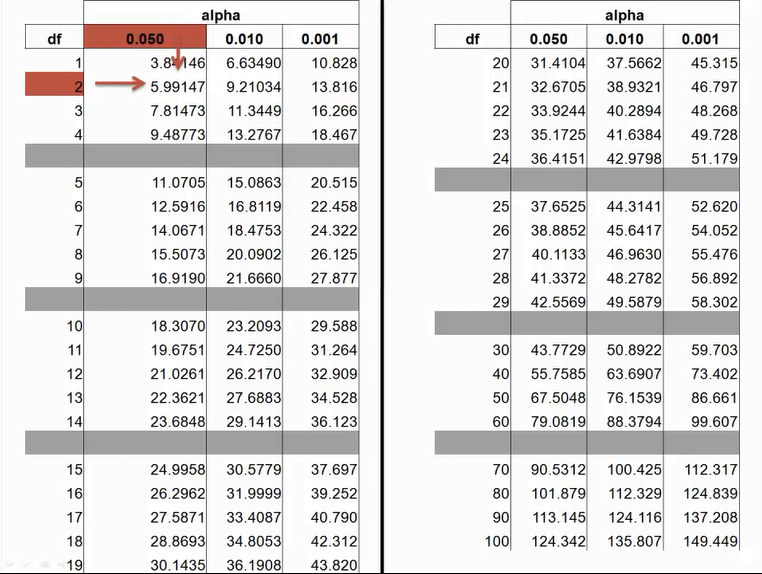
自由度：组数-1，这里有三组，自由度为3-=2

自由度为2，a=0.05,对应得关键值5.99，如果计算的值大于5.99，拒绝原假设

对数据排序，然后把对应得排序填入表内

计算公式：

T为一组的排序之和

n为一组的个数

计算的H值2.854小于5.99，不拒绝原假设

python信用评分卡建模（附代码，博主录制）

https://study.163.com/course/introduction.htm?courseId=1005214003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share