luogu2331 [SCOI2005]最大子矩阵

题目大意

　　这里有一个n*m的矩阵，请你选出其中k个子矩阵，使得这个k个子矩阵分值之和最大。注意：选出的k个子矩阵不能相互重叠。1≤n≤100,1≤m≤2,1≤k≤10。

思路

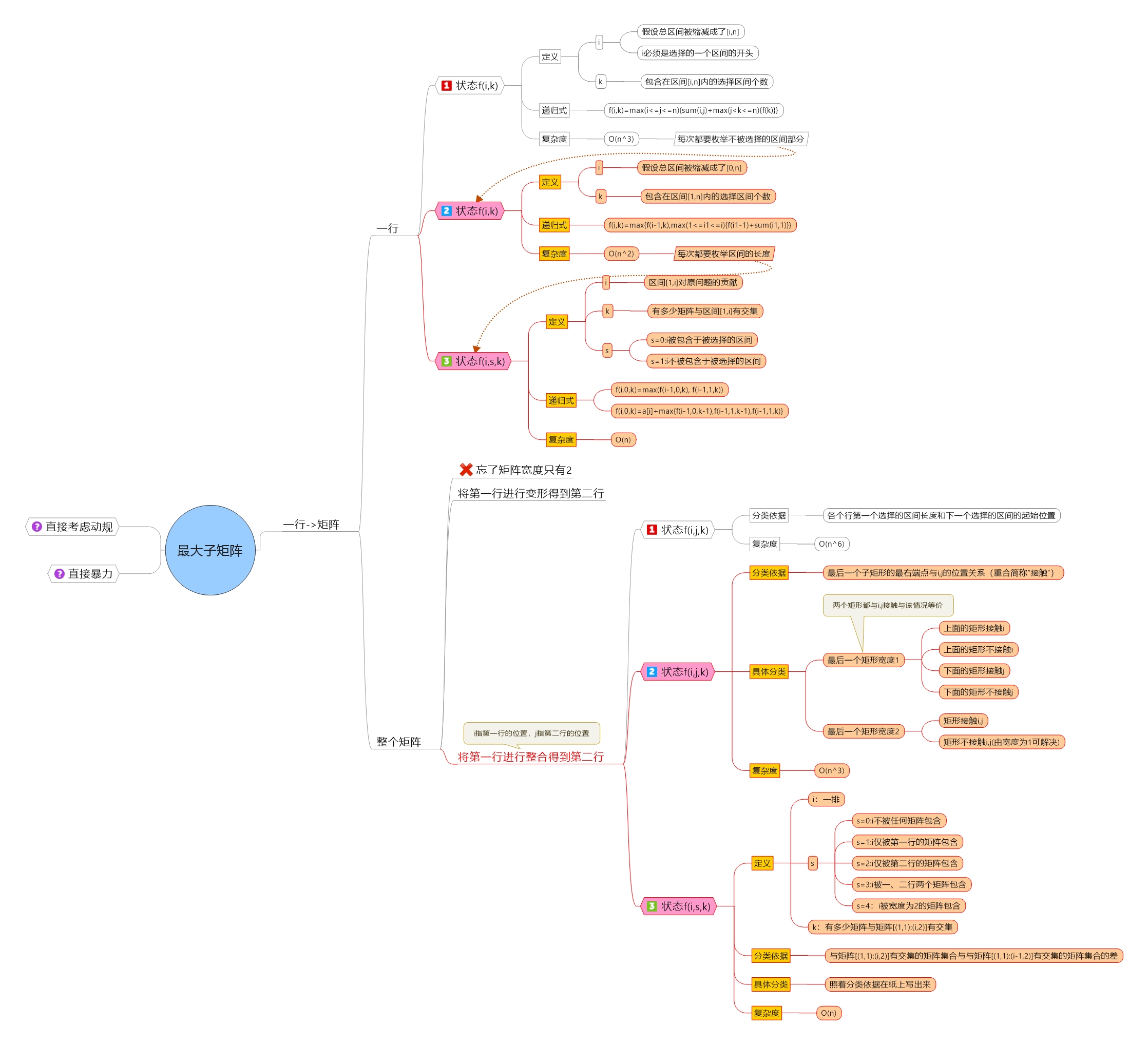
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

#define Update(x, y) x = max(x, y)
const int MAX_ROW = 110, MAX_COL = 5, MAX_K = 15, MAX_STATE = 5, MINF = 0xcfcfcfcf;
int F[MAX_ROW][MAX_STATE][MAX_K];
int A[MAX_ROW][MAX_COL];
int TotRow, TotCol, K;

int DP1()
{
	memset(F, 0xcf, sizeof(F));
	F[0][0][0] = 0;
	for (int i = 1; i <= TotRow; i++)
	{
		for (int k = 0; k <= K; k++)
		{
			Update(F[i][0][k], F[i - 1][0][k]),
			Update(F[i][0][k], F[i - 1][1][k]);

			if (k >= 1)
				Update(F[i][1][k], A[i][1] + F[i - 1][0][k - 1]),
				Update(F[i][1][k], A[i][1] + F[i - 1][1][k - 1]);
			Update(F[i][1][k], A[i][1] + F[i - 1][1][k]);
		}
	}
	return max(F[TotRow][0][K], F[TotRow][1][K]);
}

int DP2()
{
	memset(F, 0xcf, sizeof(F));
	F[0][0][0] = 0;
	for (int i = 1; i <= TotRow; i++)
		for (int k = 0; k <= K; k++)
		{
			for (int j = 0; j <= 4; j++)
				Update(F[i][0][k], F[i - 1][j][k]);

			if (k >= 1)
				for (int j = 0; j <= 4; j++)
					Update(F[i][1][k], A[i][1] + F[i - 1][j][k - 1]);
			Update(F[i][1][k], A[i][1] + F[i - 1][1][k]);
			Update(F[i][1][k], A[i][1] + F[i - 1][3][k]);

			if (k >= 1)
				for (int j = 0; j <= 4; j++)
					Update(F[i][2][k], A[i][2] + F[i - 1][j][k - 1]);
			Update(F[i][2][k], A[i][2] + F[i - 1][2][k]);
			Update(F[i][2][k], A[i][2] + F[i - 1][3][k]);

			if (k >= 2)
				for (int j = 0; j <= 4; j++)
					Update(F[i][3][k], A[i][1] + A[i][2] + F[i - 1][j][k - 2]);
			if (k >= 1)
				Update(F[i][3][k], A[i][1] + A[i][2] + F[i - 1][1][k - 1]),
				Update(F[i][3][k], A[i][1] + A[i][2] + F[i - 1][2][k - 1]);
			Update(F[i][3][k], A[i][1] + A[i][2] + F[i - 1][3][k]);

			if (k >= 1)
				for (int j = 0; j <= 4; j++)
					Update(F[i][4][k], A[i][1] + A[i][2] + F[i - 1][j][k - 1]);
			Update(F[i][4][k], A[i][1] + A[i][2] + F[i - 1][4][k]);
		}
	int ans = MINF;
	for (int i = 0; i <= 4; i++)
		Update(ans, F[TotRow][i][K]);
	return ans;
}

int main()
{
	scanf("%d%d%d", &TotRow, &TotCol, &K);
	for (int i = 1; i <= TotRow; i++)
		for (int j = 1; j <= TotCol; j++)
			scanf("%d", &A[i][j]);
	if (TotCol == 1)
		printf("%d\n", DP1());
	else
		printf("%d\n", DP2());
}

　　

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int MAX_ROW = 110, MAX_COL = 5, MAX_K = 15, MINF = 0xcfcfcfcf;
int F[MAX_ROW][MAX_ROW][MAX_K];
int A[MAX_ROW][MAX_COL];
int Sum[MAX_ROW][MAX_COL];
int TotRow, TotCol, K;

void InitSum()
{
	for (int row = 1; row <= TotRow; row++)
		for (int col = 1; col <= TotCol; col++)
			Sum[row][col] = Sum[row - 1][col] + Sum[row][col - 1] - Sum[row - 1][col - 1] + A[row][col];
}

int GetSum(int row1, int col1, int row2, int col2)
{
	return Sum[row2][col2] - Sum[row2][col1 - 1] - Sum[row1 - 1][col2] + Sum[row1 - 1][col1 - 1];
}

int DP1()
{
	memset(F, 0xcf, sizeof(F));
	F[0][0][0] = 0;
	for (int i = 1; i <= TotRow; i++)
	{
		for (int k = 0; k <= K; k++)
		{
			F[i][0][k] = F[i - 1][0][k];
			if (k >= 1)
				for (int j = 1; j <= i; j++)
					F[i][0][k] = max(F[i][0][k], F[j - 1][0][k - 1] + GetSum(j, 1, i, 1));
		}
	}
	return F[TotRow][0][K];
}

int DP2()
{
	memset(F, 0xcf, sizeof(F));
	F[0][0][0] = 0;
	for (int i = 0; i <= TotRow; i++)
	{
		for (int j = 0; j <= TotRow; j++)
		{
			for (int k = 0; k <= K; k++)
			{
				if (i >= 1)
					F[i][j][k] = max(F[i][j][k], F[i - 1][j][k]);
				if (j >= 1)
					F[i][j][k] = max(F[i][j][k], F[i][j - 1][k]);
				if (k >= 1)
				{
					for (int i1 = 1; i1 <= i; i1++)
						F[i][j][k] = max(F[i][j][k], F[i1 - 1][j][k - 1] + GetSum(i1, 1, i, 1));
					for (int j1 = 1; j1 <= j; j1++)
						F[i][j][k] = max(F[i][j][k], F[i][j1 - 1][k - 1] + GetSum(j1, 2, j, 2));
					if (i == j)
						for (int i1 = 1; i1 <= i; i1++)
							F[i][j][k] = max(F[i][j][k], F[i1 - 1][i1 - 1][k - 1] + GetSum(i1, 1, j, 2));
				}
			}
		}
	}
	return F[TotRow][TotRow][K];
}

int main()
{
	scanf("%d%d%d", &TotRow, &TotCol, &K);
	for (int i = 1; i <= TotRow; i++)
		for (int j = 1; j <= TotCol; j++)
			scanf("%d", &A[i][j]);
	InitSum();
	if (TotCol == 1)
		printf("%d\n", DP1());
	else
		printf("%d\n", DP2());
}