树状数组（Binary Indexed Tree）

　　树状数组（Binary Indexed Tree，BIT） 是能够完成下述操作的数据结构。

　　给一个初始值全为 0 的数列 a1, a2, ..., an

　　（1）给定 i，计算 a1+a2+...+ai

　　（2）给定 i 和 x，执行 ai += x

1.基于线段树的实现

　　如果使用线段树，只需要做少许修改就可以实现这两个功能。线段树的每个节点上维护的是对应区间的和。

　　

　　接下来看如何计算从 s 到 t 的和（a_s + a_s+1 + ... + a_t）。在基于线段树的实现这个和是可以直接求得的。

　　但是如果我们能够计算（从 1 到 t 的和） - （从 1 到 s - 1 的和），同样可以得到 s 到 t 的和。也就是说，只要对于任意 i，我们都能计算出 1 到 i 的部分和就可以了。

　　可以发现，线段树上的每个节点的右儿子的值都不需要了（在计算时如果要使用这个点的值，那么它的左边的兄弟的值也一定会用到，这个时候只需要使用它们的父亲的值就可以了）。

　　

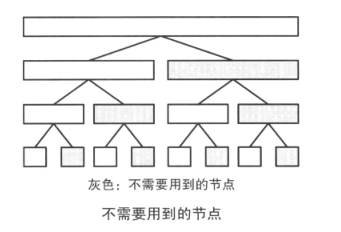
　　基于上面的思路得到的数据结构就是 BIT。比起线段树，BIT实现起来更方便，速度也更快。

2. BIT的结构

　　BIT 使用数组维护下图所示的部分和

　　

　　也就是把线段树中不需要的节点去掉之后，再把剩下的节点对应到数组中。对比每个节点对应的区间的长度和节点编号的二进制表示。以 1 结尾的 1， 3， 5， 7 的长度是1， 最后有 1 个 0 的2， 6 的长度是2，最后有两个 0 的 4 的长度是 4 .... 这样，编号的二进制表示就能够和区间非常容易地对应起来。利用这个性质，BIT 可以通过非常简单的位运算实现。

3. BIT的求和

　　计算前 i 项的和需要从 i 开始，不断把当前位置 i 的值加入到结果中， 并从 i 中减去 i 的二进制最低非 0 位对应的幂，直到 i 变为 0 为止。i 的二进制的最后一个 1 可以通过 i & - i 得到。

　　

4.BIT的值的更新

　　使第 i 项的值增加 x 需要从 i 开始，不断把当前位置 i 的值增加 x， 并把 i 的二进制最低非 0 位对应的幂加到 i 上。

　　　

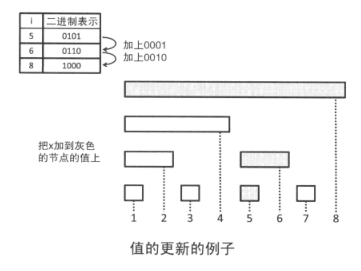
5. BIT的复杂度

　　总共需要对O（log n）个值进行操作，所以复杂度是O（log n）。

6. BIT的实现

　　提一下 i -= i & -i 可以写为 i = i &（i - 1）

// [1, n]
int bit[MAX_N + ], n;

int sum(int i) {
    int s = ;
    while (i > ) {
        s += bit[i];
        i -= i & -i;
    }
    return s;
} 

void add(int i, int x) {
    while (i <= n) {
        bit[i] += x;
        i += i & -i;
    }
}

　　//本来想把代码补完整的。。参考线段树就行，但是后面会有综述我就不补了

7.  二维BIT

　　BIT 可以方便地扩展到二维的情况。对于 W * H 的二维 BIT 只需建立 H 个大小为 x 轴方向元素个数 W 的 BIT，然后把这些 BIT 通过 y 轴方向的 BIT 管理起来就可以了。也就是说，y 轴方向的 BIT 的每个元素不是整数，而是一个 x 轴方向的 BIT。这样所有的操作的复杂度都是 O（log W * log H）。用同样的方法可扩展到更高的维度。

　　// emm

8. 需要运用 BIT 的问题

　　

　　

　　冒泡排序的复杂度是 O（n²），所以无法模拟过程。选用适当的数据结构可以解决这个问题。

　　所求的交换次数等价于 满足 i < j , a_i > a_j  的 i  的个数，（这种数对的个数叫做逆序数）。而对于每一个 j，如果能够快速求出满足 i < j, a_i > a_j  的 i  的个数，那么问题就解决了。我们构建一个值的范围是 1 ~ n 的 BIT，按照 j = 0， 1， 2， ...， n-1 的顺序进行如下操作。

　　（1）把 j - （BIT查询得到的前 a_j 项的和）加到答案中

　　（2）把 BIT 中 a_j 位置上的值加 1

　　对于每一个 j， （BIT查询得到的前 a_j 项的和）就是满足i < j , a_i > a_j  的 i  的个数。因此把这个值从 j 中减去之后，得到的就是满足 i < j , a_i > a_j  的 i  的个数。由于对于每一个 j 的复杂度是O（log n），所以整个算法的复杂度是O（n log n）。

　　// 但实际上实现计算逆序数更简单的算法是通过分治思想利用归并排序计算

typedef long long ll;
int n, a[MAX_N];
//省略BIT部分代码
void solve() {
    ll ans = ;
    for (int j = ; j < n; j++) {
        ans += j - sum(a[j]);
        add(a[j], );
    }
    printf("%lld\n", ans);
} 

　　

　　树状数组可以高效地求出连续的一段元素之和或者更新单个元素的值。但是无法高效地给某一个区间里的所有元素同时加上一个值。因此，本题无法直接使用树状数组。在这里先考虑利用线段树来求解，然后再考虑改造树状数组来求解。

　　对于每个节点，维护有该节点对应的区间的和，那么就可以在 O（log n）时间内求出任意区间的和。但这样就没有办法高效地实现对一个区间同时加一个值，因为需要对这个区间相关的所有节点都进行更新才可以。

　　为了保持线段树的高效，对于每个节点我们维护以下两个数据

　　（1）给这个节点对应的区间内的所有元素共同加上的值

　　（2）在这个节点对应的区间中除去（1）之外其他的值的和

　　通过单独维护共同加上的值，给区间同时加上一个值的操作就可以高效地进行了。如果对于父亲节点同时加了一个值，那么这个值就不会在儿子节点被重复考虑。在递归计算和时再把这一部分的值加到结果里面就可以了。这样，不论是同时加一个值还是查询一段的和的复杂度都是O（log n）。

　　（1）T 是操作的种类。第 i 个操作的 T[ i ] 是 C 的话，就是给区间同时加上一个值，是 Q 的话则是查询一段的和。

　　（2）A， L， R 都是以 0 为下标起点的。

　　

typedef long long ll;
const int DAT_SIZE = ( << ) - ;

int N, Q;
int A[MAX_N];
char T[MAX_Q];
int L[MAX_Q], R[MAX_Q], X[MAX_Q];

// 线段树
ll data[DATA_SIZE], datb[MAX_SIZE];

// 对区间[a, b]同时加 x
// k 是节点的编号，对应的区间是（l， r）
void add(int a, int b, int x, int k, int l, int r) {
    if (a <= l && r <= b)
        data[k] += x;
    else if (l < b && a < r) {
        datb[k] += (min(b, r) - max(a, l)) * x;
        add(a, b, x, k *  + , l, (l + r) / );
        add(a, b, x, k *  + , (l + r) / , r);
    }
}

// 对区间[a, b]同时加 x
// k 是节点的编号，对应的区间是（l， r）
ll sum(int a, int b, int k, int l, int r) {
    if (b <=  || r <= a) return ;
    else if (a <=  && r <= b) return data[k] * (r - ) + data[k];
    else {
        ll res = (min(b, r) - max(a, l)) * data[k];
        res += sum(a, b, k *  + , l, (l + r) / );
        res += sum(a, b, k *  + , (l + r) / , r);
        return res;
    }
}

void solve() {
    for (int i = ; i < N; i++)
        add(i, i + , A[i], , , N);
    for (int i = ; i < Q; i++) {
        if (T[i] == 'C')
            add(L[i], R[i] + , X[i], , , N);
        else
            printf("%lld\n", sum(L[i], R[i] + , , , N));
    }
}

未完待续