二叉堆 与 PriorityQueue

堆在存储器中的表示是数组，堆只是一个概念上的表示。堆的同一节点的左右子节点都没有规律。

堆适合优先级队列（默认排列顺序是升序排列，快速插入与删除最大/最小值）。

数组与堆

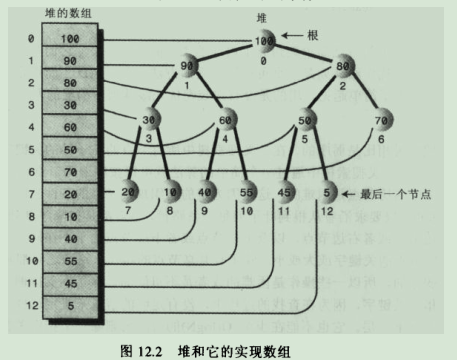
堆（完全二叉树）（构造大顶堆或者小顶堆的时间复杂度：O(logn)）

堆实现的优先级队列虽然和数组实现相比删除慢了些，但插入的时间快的多了：
	当速度很重要且有很多插入操作时，可以选择堆来实现优先级队列。
	堆插入删除的效率：时间复杂度是：O(logn)。

小顶堆：父节点的值 <= 左右孩子节点的值
大顶堆：父节点的值 >= 左右孩子节点的值

堆的定义：n个关键字序列array[0，...，n-1]：

	若array[0，...，n-1]表示一颗完全二叉树的顺序存储模式，则双亲节点指针和孩子结点指针之间的内在关系如下：

		任意一节点指针 i（0 <= i <= (n-1)/2） ： 父节点：i==0 ? null : (i-1)/2

				左孩子：2*i + 1

				右孩子：2*i + 2

	① array[i] <= array[2*i + 1] 且 array[i] <= array[2*i + 2] ： 称为小根堆

	② array[i] >= array[2*i + 1] 且 array[i] >= array[2*i + 2] ： 称为大根堆

堆的插入( add(e)，offer(e) )：添加到末尾，由于可能破坏堆结构，需要调整（向上筛选）

	插入使用向上筛选，向上筛选的算法比向下筛选的算法相对简单，因为它不需要比较两个子节点关键字值的大小

删除操作 ( remove(o) )：由于可能破坏堆结构，需要调整（向下筛选）

删除堆顶 ( poll() )：由于可能破坏堆结构，需要调整（向下筛选）

	移除是指删掉关键字值最大的节点，即根节点。

　　在被筛选节点的每个暂时停留的位置，向下筛选的算法总是要检查哪一个子节点更大，然后目标节点和较大的子节点交换位置

堆排序（时间复杂度：O(nlogn)）

堆排序是一种树形选择排序方法，它的特点是：
	在排序的过程中，将array[0，...，n-1]看成是一颗完全二叉树的顺序存储结构，
	利用完全二叉树中双亲节点和孩子结点之间的内在关系，在当前无序区中选择关键字最大（最小）的元素。

步骤：
    构造堆
    固定最大值再构造堆（将最大值元素（堆头）与堆尾元素交换，将其他数再构造成最大堆）
    重复上述过程

堆（二叉堆）排序的时间复杂度，最好，最差，平均都是O(nlogn)，空间复杂度O(1)，是不稳定的排序。

PriorityQueue

public class PriorityQueue<E> extends AbstractQueue<E>
    implements java.io.Serializable {

    private static final long serialVersionUID = -7720805057305804111L;

    private static final int DEFAULT_INITIAL_CAPACITY = 11;

    transient Object[] queue; // non-private to simplify nested class access

    int size;

    private final Comparator<? super E> comparator;

    transient int modCount;     // non-private to simplify nested class access

    public PriorityQueue(Collection<? extends E> c) {}	//使用已有集合构建二叉堆

    public PriorityQueue() {
        this(DEFAULT_INITIAL_CAPACITY, null);
    }

    public PriorityQueue(int initialCapacity,
                         Comparator<? super E> comparator) {

        if (initialCapacity < 1)
            throw new IllegalArgumentException();
        this.queue = new Object[initialCapacity];
        this.comparator = comparator;
    }
}

//自定义比较器，降序排列
static Comparator<Integer> cmp = new Comparator<Integer>() {
	public int compare(Integer e1, Integer e2) {
		return e2 - e1;
	}
};

在未排序的数组中找到第 k 个最大的元素

/**
 * 示例 1:
 *     输入: [3,2,1,5,5,4] 和 k = 2
 *     输出: 5
 *
 * 时间复杂度 : O(Nlogk)。
 * 空间复杂度 : O(k)，用于存储堆元素。
 */

/**
 * 小顶堆
 */
class Solution {
    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> pq = new PriorityQueue<>();
        for (int i = 0; i < nums.length; i++) {
            pq.add(nums[i]);
            if(pq.size()>k)pq.poll();
        }
        return pq.poll();
    }
}

找出动态有序列表的中位数

/**
 * 中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。
 *
 * 例如，
 *     [2,3,4] 的中位数是 3
 *     [2,3] 的中位数是 (2 + 3) / 2 = 2.5
 *
 * 方法：最大堆与最小堆。
 *     思路：各存储一半，最大堆的堆顶比最小堆的堆顶小。
 *
 * 时间复杂度：O(logN)，从堆里得到一个 “最值” 而其它元素无需排序
 * 空间复杂度：O(N)
 */
class MedianFinder1 {
    /**
     * 当前大顶堆和小顶堆的元素个数之和
     */
    private int count;
    private PriorityQueue<Integer> maxheap;
    private PriorityQueue<Integer> minheap;

    /**
     * initialize your data structure here.
     */
    public MedianFinder1() {
        count = 0;
        maxheap = new PriorityQueue<>((x, y) -> y - x); //大顶堆
        minheap = new PriorityQueue<>();    //小顶堆
    }

    public void addNum(int num) {
        count += 1;
        maxheap.offer(num);
        minheap.add(maxheap.poll());
        // 如果两个堆合起来的元素个数是奇数，小顶堆要拿出堆顶元素给大顶堆
        if ((count & 1) != 0) {
            maxheap.add(minheap.poll());
        }
    }

    public double findMedian() {
        if ((count & 1) == 0) {
            // 如果两个堆合起来的元素个数是偶数，数据流的中位数就是各自堆顶元素的平均值
            return (double) (maxheap.peek() + minheap.peek()) / 2;
        } else {
            // 如果两个堆合起来的元素个数是奇数，数据流的中位数大顶堆的堆顶元素
            return (double) maxheap.peek();
        }
    }
}

最强堆排序文章

https://blog.csdn.net/u010452388/article/details/81283998