Educational DP Contest H - Grid 1 (DP)

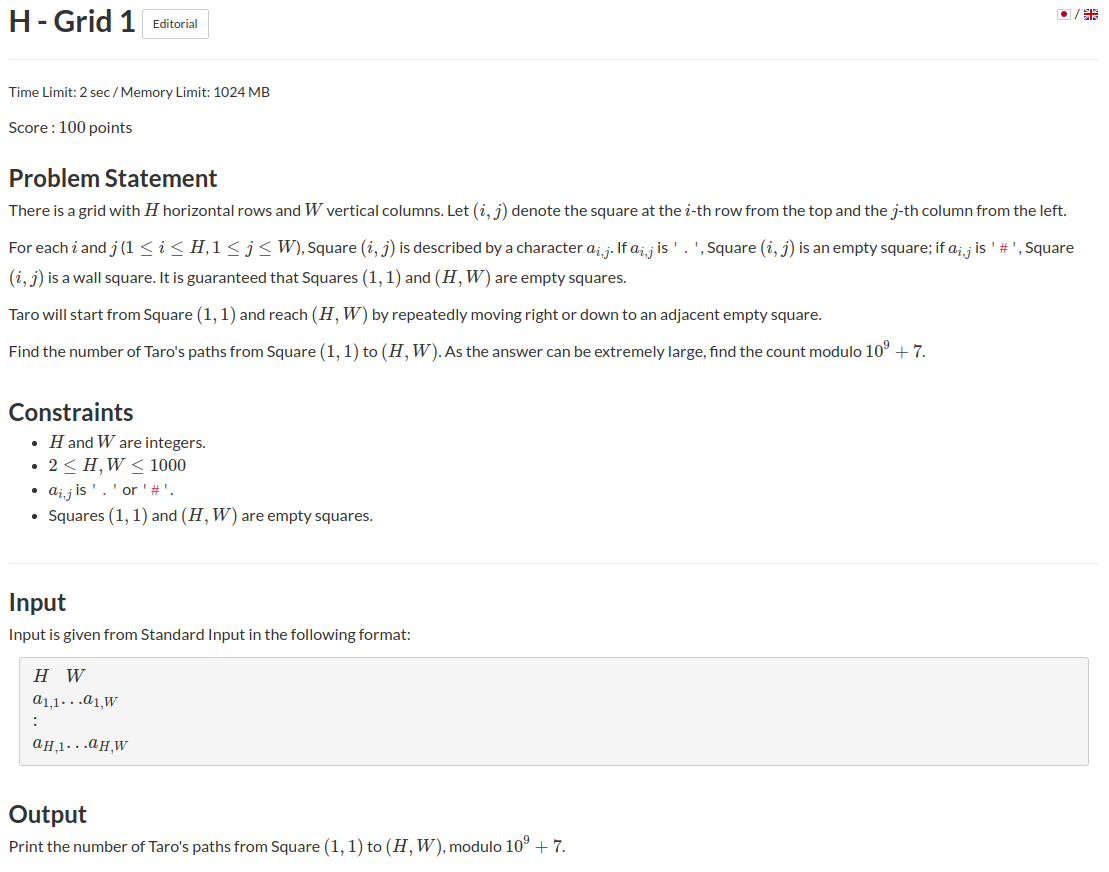
• 题意:有一个\(n\)X\(m\)的图,"#"表示障碍物,"."表示道路,只能向右或向下走,问从左上角走到右下角的方案数.

• 题解:这题可以用bfs来搞,但dp更简单点吧～～.首先,只有当向右和向下都能走时,方案数才会增加,我们用dp表示从起点走到某个单位的方案数,这个单位只能从左边或上边走过来,所以它的方案数就是\(dp[i][j]=dp[i][j-1]+dp[i-1][j]\),遍历一下即可.

• 代码:

  int n,m;
  char s[2000][2000];
  int dp[2000][2000];
  
  int main() {
      //ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  	n=read();
  	m=read();
  
  	for(int i=1;i<=n;++i){
  		scanf("%s",s[i]+1);
  	}
  
  	dp[1][1]=1;
  
  	for(int i=1;i<=n;++i){
  		for(int j=1;j<=m;++j){
  			if(s[i][j]!='#' && i+j!=2){
  				dp[i][j]=dp[i-1][j]+dp[i][j-1];
  				dp[i][j]%=mod;
  			}
  		}
  	}
  
  	printf("%d\n",dp[n][m]);
  
      return 0;
  }