Spark MLlib聚类KMeans

算法说明

　　聚类（Cluster analysis）有时也被翻译为簇类，其核心任务是：将一组目标object划分为若干个簇，每个簇之间的object尽可能相似，簇与簇之间的object尽可能相异。聚类算法是机器学习（或者说是数据挖掘更合适）中重要的一部分，除了最为简单的K-Means聚类算法外，比较常见的还有层次法（CURE、CHAMELEON等）、网格算法（STING、WaveCluster等），等等。　　

　　较权威的聚类问题定义：所谓聚类问题，就是给定一个元素集合D，其中每个元素具有n个可观察属性，使用某种算法将D划分成k个子集，要求每个子集内部的元素之间相异度尽可能低，而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇。

　　K-means聚类属于无监督学习，以往的回归、朴素贝叶斯、SVM等都是有类别标签y的，也就是说样例中已经给出了样例的分类。而聚类的样本中却没有给定y，只有特征x，比如假设宇宙中的星星可以表示成三维空间中的点集。聚类的目的是找到每个样本x潜在的类别y，并将同类别y的样本x放在一起。比如上面的星星，聚类后结果是一个个星团，星团里面的点相互距离比较近，星团间的星星距离就比较远了。

　　与分类不同，分类是示例式学习，要求分类前明确各个类别，并断言每个元素映射到一个类别。而聚类是观察式学习，在聚类前可以不知道类别甚至不给定类别数量，是无监督学习的一种。目前聚类广泛应用于统计学、生物学、数据库技术和市场营销等领域，相应的算法也非常多。

实例介绍

　　在该实例中将介绍K-Means算法，K-Means属于基于平方误差的迭代重分配聚类算法，其核心思想十分简单：

随机选择K个中心点；
计算所有点到这K个中心点的距离，选择距离最近的中心点为其所在的簇；
简单地采用算术平均数（mean）来重新计算K个簇的中心；
重复步骤2和3，直至簇类不再发生变化或者达到最大迭代值；
输出结果。

　　K-Means算法的结果好坏依赖于对初始聚类中心的选择，容易陷入局部最优解，对K值的选择没有准则可依循，对异常数据较为敏感，只能处理数值属性的数据，聚类结构可能不平衡。

　　本实例中进行如下步骤：

　　　　1.装载数据，数据以文本文件方式进行存放；

　　　　2.将数据集聚类，设置2个类和20次迭代，进行模型训练形成数据模型；

　　　　3.打印数据模型的中心点；

　　　　4.使用误差平方之和来评估数据模型；

　　　　5.使用模型测试单点数据；

　　　　6.交叉评估1，返回结果；交叉评估2，返回数据集和结果。

测试数据说明

　　该实例使用的数据为kmeans_data.txt，可以在本系列附带资源/data/class8/目录中找到。在该文件中提供了6个点的空间位置坐标，使用K-means聚类对这些点进行分类。

　　使用的kmeans_data.txt的数据如下所示：

0.0 0.0 0.0

0.1 0.1 0.1

0.2 0.2 0.2

9.0 9.0 9.0

9.1 9.1 9.1

9.2 9.2 9.2

程序代码

import org.apache.log4j.{Level, Logger}

import org.apache.spark.{SparkConf, SparkContext}

import org.apache.spark.mllib.clustering.KMeans

import org.apache.spark.mllib.linalg.Vectors

object Kmeans {

  def main(args: Array[String]) {

    // 屏蔽不必要的日志显示在终端上

    Logger.getLogger("org.apache.spark").setLevel(Level.WARN)

    Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)

    // 设置运行环境

    val conf = new SparkConf().setAppName("Kmeans").setMaster("local[4]")

    val sc = new SparkContext(conf)

    // 装载数据集

    val data = sc.textFile("/home/hadoop/upload/class8/kmeans_data.txt", )

    val parsedData = data.map(s => Vectors.dense(s.split(' ').map(_.toDouble)))

    // 将数据集聚类，2个类，20次迭代，进行模型训练形成数据模型

    val numClusters =

    val numIterations =

    val model = KMeans.train(parsedData, numClusters, numIterations)

    // 打印数据模型的中心点

    println("Cluster centers:")

    for (c <- model.clusterCenters) {

      println("  " + c.toString)

    }

    // 使用误差平方之和来评估数据模型

    val cost = model.computeCost(parsedData)

    println("Within Set Sum of Squared Errors = " + cost)

    // 使用模型测试单点数据

println("Vectors 0.2 0.2 0.2 is belongs to clusters:" + model.predict(Vectors.dense("0.2 0.2 0.2".split(' ').map(_.toDouble))))

println("Vectors 0.25 0.25 0.25 is belongs to clusters:" + model.predict(Vectors.dense("0.25 0.25 0.25".split(' ').map(_.toDouble))))

println("Vectors 8 8 8 is belongs to clusters:" + model.predict(Vectors.dense("8 8 8".split(' ').map(_.toDouble))))

    // 交叉评估1，只返回结果

    val testdata = data.map(s => Vectors.dense(s.split(' ').map(_.toDouble)))

    val result1 = model.predict(testdata)

    result1.saveAsTextFile("/home/hadoop/upload/class8/result_kmeans1")

    // 交叉评估2，返回数据集和结果

    val result2 = data.map {

      line =>

        val linevectore = Vectors.dense(line.split(' ').map(_.toDouble))

        val prediction = model.predict(linevectore)

        line + " " + prediction

    }.saveAsTextFile("/home/hadoop/upload/class8/result_kmeans2")

    sc.stop()

  }

}

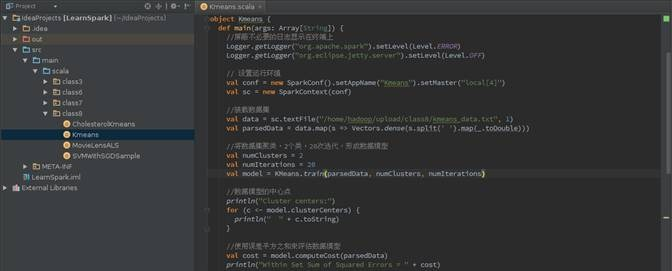
IDEA执行情况

　　第一步使用如下命令启动Spark集群

$cd /app/hadoop/spark-1.1.

$sbin/start-all.sh

　　第二步在IDEA中设置运行环境

　　在IDEA运行配置中设置Kmeans运行配置，由于读入的数据已经在程序中指定，故在该设置界面中不需要设置输入参数

　第三步执行并观察输出

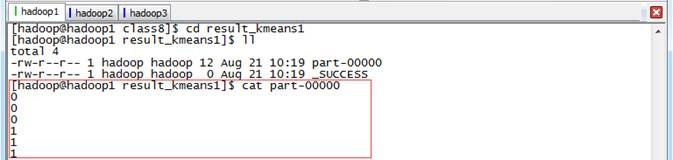
　　在运行日志窗口中可以看到，通过计算计算出模型并找出两个簇中心点：(9.1，9.1，9.1)和(0.1，0.1，0.1)，使用模型对测试点进行分类求出分属于族簇。

　第四步查看输出结果文件

　　在/home/hadoop/upload/class8目录中有两个输出目录：

　　查看结果1，在该目录中只输出了结果，分别列出了6个点所属不同的族簇

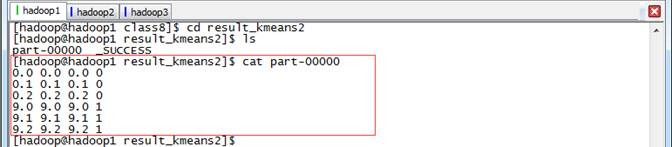
　　查看结果2，在该目录中输出了数据集和结果