poj1417 True Liars[并查集+背包]

有一点小转化的题，在设计dp状态时还是有点费脑筋的。

地址。

---

依题意，首先可以知道肯定要扩展域的并查集（明摆着的嘛）。一个"好人"域，一个"坏人"域，每句话分两种情况考虑连边。假设是yes，同域连边，否则异域连边（经典模型嘛）。然后就是要考虑如何验证是否有$x$个好人$y$个坏人的唯一解存在。这取决于联通块。

可以参考我瞎画的图，上面点1~N,下面点N+1~2N。

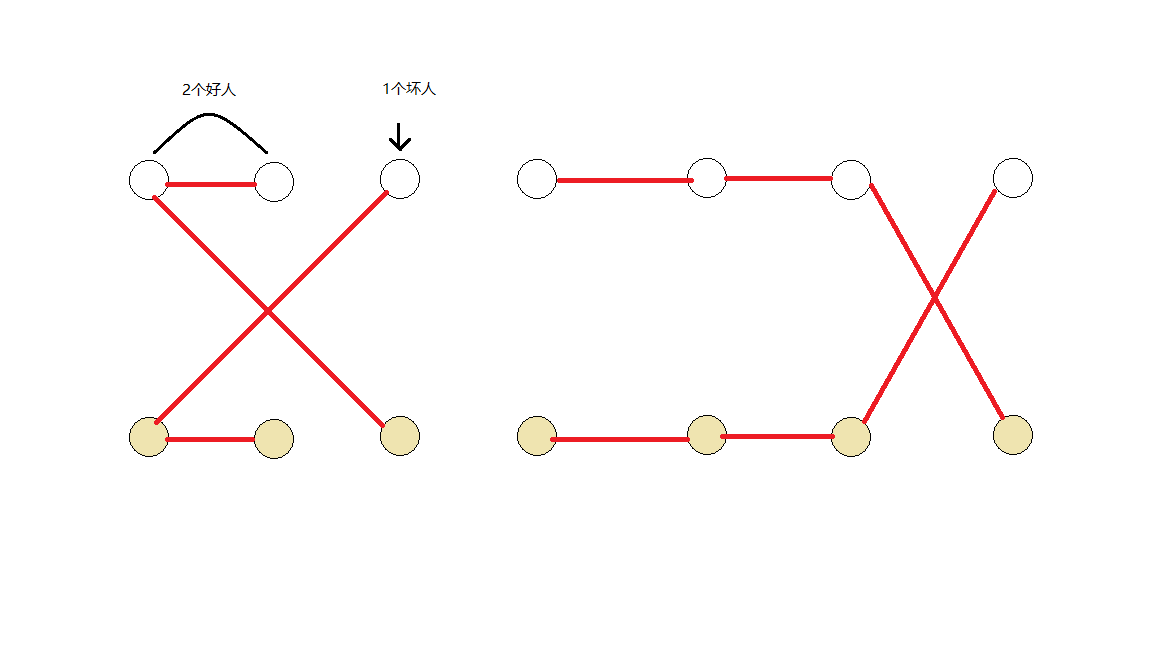
由于并查集合并时操作的对称性，可以发现一个联通块要么$x$个好人$y$个坏人要么$y$个好人$x$个坏人。那么对于所有联通块必须选其中一种方案，最后要凑齐。于是我就想到二维的背包。。但是复杂度太大了啊。。卡了好久，于是又手玩了样例。发现当我所有联通块恰好凑出x个好人时，剩下的不就全是坏人吗。所以只要去做一个好人的背包就行了。dp的时候由于没处理好关于多解的问题，又调了半小时。。一题做两个小时我也是醉了。。其实就是有前面一个状态转移，记一下$pre$。在记一下方案。最终好人的背包装满的状态方案不是1种就是无解，是一种就把所有好人找出来，这个我开了vector存了每个联通块。细节还看code，虽然可能写繁掉了qwq。。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #include<queue>
 #include<vector>
 #define dbg(x) cerr<<#x<<" = "<<x<<endl
 #define ddbg(x,y) cerr<<#x<<" = "<<x<<"   "<<#y<<" = "<<y<<endl
 using namespace std;
 typedef long long ll;
 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,:;}
 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,:;}
 template<typename T>inline T _min(T A,T B){return A<B?A:B;}
 template<typename T>inline T _max(T A,T B){return A>B?A:B;}
 template<typename T>inline T read(T&x){
     x=;int f=;char c;while(!isdigit(c=getchar()))if(c=='-')f=;
     while(isdigit(c))x=x*+(c&),c=getchar();return f?x=-x:x;
 }
 const int N=+;
 int fa[N<<],f[N][N>>],cnt[N][N>>],pos[N],tot,tot2,ans[N];
 vector<int> a[N],b[N];
 int n,m,gd,bd,x,y;
 inline int Get(int x){return fa[x]^x?fa[x]=Get(fa[x]):x;}

 int main(){//freopen("test.in","r",stdin);//freopen("test.out","w",stdout);
     while(read(m),read(gd),read(bd),m||gd||bd){
         n=gd+bd;char s[];tot=,tot2=;memset(pos,,sizeof pos);
         for(register int i=;i<=n;++i)a[i].clear(),b[i].clear();
         for(register int i=;i<=(n<<);++i)fa[i]=i;
         for(register int i=;i<=m;++i){
             read(x),read(y),scanf("%s",s);
             if(x==y)continue;
             if(s[]=='y')fa[Get(x)]=Get(y),fa[Get(x+n)]=Get(y+n);
             else fa[Get(x)]=Get(y+n),fa[Get(x+n)]=Get(y);
         }
         for(register int i=;i<=n;++i)if(Get(i)<=n)a[Get(i)].push_back(i);
         for(register int i=n+;i<=(n<<);++i)if(Get(i)<=n)b[Get(i)].push_back(i-n);
         for(register int i=;i<=n;++i)if(!a[i].empty()||!b[i].empty())pos[++tot]=i;//联通块统计
         memset(f,,sizeof f);memset(cnt,,sizeof cnt);cnt[][]=;
         for(register int i=;i<=tot;++i){
             x=a[pos[i]].size(),y=b[pos[i]].size();
             for(register int j=,lx=j-x,ly=j-y;j<=gd;++j,lx=j-x,ly=j-y){
                 if(lx<&&ly>=)f[i][j]=ly,cnt[i][j]=cnt[i-][ly];
                 else if(lx>=&&ly<)f[i][j]=lx,cnt[i][j]=cnt[i-][lx];
                 else if(lx>=&&ly>=)f[i][j]=cnt[i-][lx]?lx:ly,cnt[i][j]=cnt[i-][lx]+cnt[i-][ly];
             }
         }//做dp
         if(cnt[tot][gd]^)printf("no\n");
         else{
             int j=gd;
             while(tot){
                 if(j-f[tot][j]==a[pos[tot]].size()){for(register int i=;i<a[pos[tot]].size();++i)ans[++tot2]=a[pos[tot]][i];}
                 else for(register int i=;i<b[pos[tot]].size();++i)ans[++tot2]=b[pos[tot]][i];
                 j=f[tot--][j];
             }//推回去
             sort(ans+,ans+tot2+);
             for(register int i=;i<=tot2;++i)printf("%d\n",ans[i]);
             printf("end\n");
         }
     }
     return ;
 }