【机器学习】Linear least squares, Lasso,ridge regression有何本质区别？

Linear least squares, Lasso,ridge regression有何本质区别？

Linear least squares, Lasso,ridge regression有何本质区别？

还有ridge regression uses
L2 regularization; and Lasso uses
L1 regularization.

L1和L2一般如何选取？

我觉得这个问题首先要从“为什么普通的线性回归在很多场合不适用”开始说起，要理解这个问题一定要把大一线性代数里“空间”的概念掌握好。

首先，普通的线性回归的公式是这样的

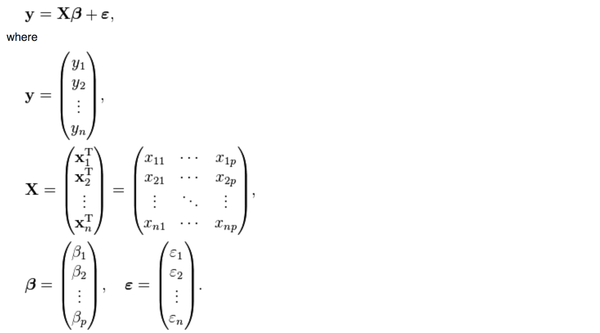y是被解释变量，X是p个解释变量，我们手里有n组(y,
X)的样本，然后想要通过这些样本找到一个向量beta使得

被最小化，满足这个最小化条件的beta就是线性回归要寻找的beta，数学上可以证明这个问题是有通解的：

也就是说，只有我们手里有X和Y这两个矩阵（向量），把它们带入上面的公式就能得到我们想要的beta，然后就能用beta和新的Xi来对未知的Yi进行预测了。

然而，上面这个公式有一个问题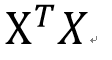，这两个矩阵相乘的结果，一个p*p的矩阵(p是解释变量的个数)，一定是可逆的吗？不可逆的话刚才算beta的公式不就没有意义了吗？

幸运的是，在实际生活中，只要我们的数据真的是随机抽取的，这个矩阵一般都是可逆的。

不幸的是，有一种存在叫做almost singular。

一个方阵(行数=列数, 比如上面那个p*p矩阵)一定可以被归类到以下两种情况：

singular: 行列式|X|=0，特征根中至少有一个是0，不满秩，不可以求逆。

nonsingular: 行列式|X|不等于0，特征根都不等于0，满秩，可以求逆。

这个矩阵

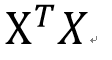肯定是nonsingular的可以求逆，但是在一些情况下（比如multicollinearity），这个矩阵的行列式的值可能非常非常非常小(比如0.000000001)，于是X只要有一个微小的变化，它的逆矩阵就会有一个很大很大的变化，导致你用不同的样本估计出来的beta的差别非常非常大，这样的矩阵就叫almost
singular。

almost singular: 行列式|X|几乎等于0，特征根有一个或多个接近于0，满秩，可以求逆，但是对X进行微小的改变会导致逆矩阵发生巨大的改变。

大家想一想，如果你用1点钟收集到的数据估出来的参数等于100，3点钟收集到的数据估出来的参数等于100000，那你到底要用哪一个？到底哪一个是对的？你并不知道。

这个问题就是楼上有人提出的“estimator 的数值解可能不存在／极不稳定”的情况。

那么如何解决呢？当然要对症下药啦。既然这个矩阵的行列式近似等于0，那我在它的对角线上全部加上一个常数不就行了嘛？

于是ridge regression就被发明出来了：

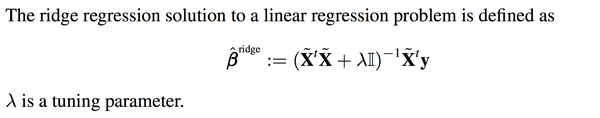其实就是在刚刚Beta的解的公式的基础上进行了微小的调整，I是单位矩阵，lamda是通过cross
validation来确定的，并不是需要估计的参数。这个调整就是楼上有人说的regularization。

你可能会很疑惑，如果说线性回归是在最小化下面这个方程：

那ridge
regression是在最小化什么东西呢？数学上也可以证明，上面新的beta的解，其实就是在最小化下面这个式子：

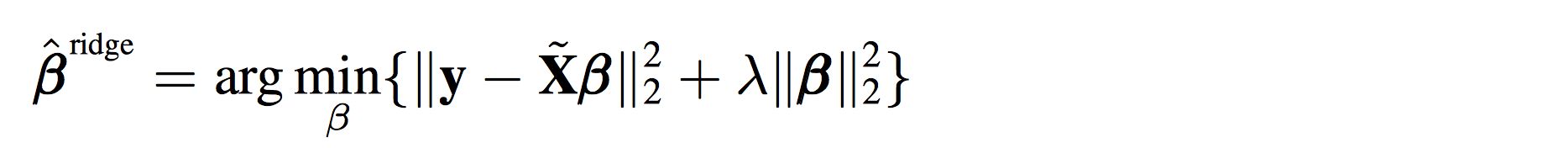其实就是在上面的式子后面多加了一项而已。

你可能又要问了，多加的那一项凭什么是模长呢？不能把2-norm改成1-norm吗？

答案是可以的，这种情况就是lasso了：



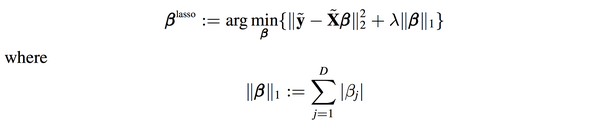
遗憾的是，lasso是不能像ridge regression和linear regression一样写出“显式解”的，必须用数值方法去近似上面的优化问题的解。

幸运的是，统计学家发现用lasso算出来的beta的很多项是0，也就是说你在估计参数的时候顺带着把model selection也一起做了，买一送一哦亲！

为什么会这样呢？上面有答主传了一副图：

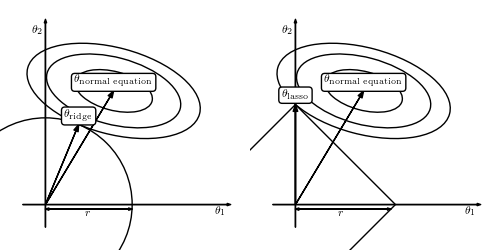因为lasso选了1-norm，导致theta-lasso的范围“有棱有角”，在和normal
equation“相互妥协”的过程中万一碰到了“楞”或者“角”的话，就会有一个解释变量的参数变成0。比如右图中的theta1就变成了0。而左图是无论如何不可能让某个参数变成0的。



简而言之，

不想做数值优化，想要一个确定的解，选ridge regression吧！

不想做完参数估计还要做model selection挑选变量，选lasso吧！

可是新的问题又出现了，ridge regression选了2-norm，lasso选了1-norm，那我能不能把这个问题拓展到p-norm的情形呢？(这个p和刚才的解释变量的个数p是两个概念)

答案是可以的，只要p大于等于1就行了。

p为什么不能小于1？因为p小于1时刚才那幅图里的圆形和正方形会继续“往里陷”，变成下面的样子：

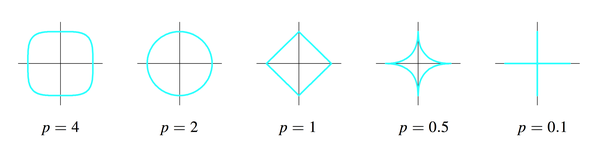这样这个集合就不是convex
set了，没有办法做最优化了，which is another long story。



最后回到一开始“空间”的问题，为什么我说理解这个问题“空间”的概念非常重要呢？

其实线性回归的本质，是把一个n维空间的向量Y投射到p+1维空间，这个p+1维空间就是p个X解释变量和一个常数向量，这p+1个向量span出来的一个“亚空间”。因为Y本身在n维空间太复杂了，而我们生活在p+1维空间（一般情况下p+1远小于n），我们能做的就是把Y投射到我们所在的p+1维空间，尽可能的去获得更多的Y的信息。然而，有些时候因为X数据本身出现了一些问题，p+1维空间发生了“退化”或者“坍塌”，为了“支撑”起这个空间，我们在对角线上都加了一个常数，撑起了一个新的空间，这就是regularization的基本思路。

你可能又要问了，有没有可能不用投射到p+1维空间，我们直接在n维空间找到Y的全部信息呢？

答案是可以的，但是这就不叫线性回归了，这叫解线性方程组(p+1=n)。

所以说，线性代数真的很重要啊。