P5030 长脖子鹿放置

题目背景

众周所知，在西洋棋中，我们有城堡、骑士、皇后、主教和长脖子鹿。

题目描述

如图所示，西洋棋的“长脖子鹿”，类似于中国象棋的马，但按照“目”字攻击，且没有中国象棋“别马腿”的规则。（因为长脖子鹿没有马腿）

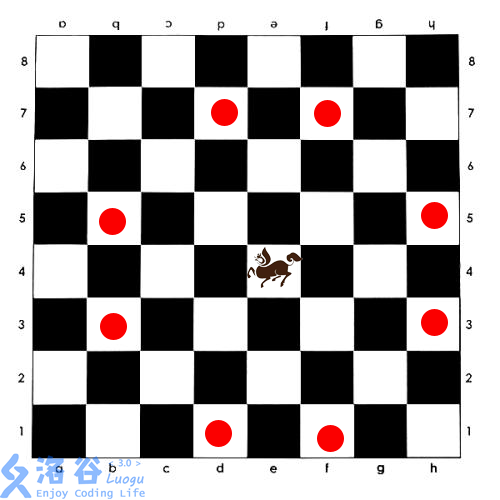
给定一个N * M,的棋盘，有一些格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的长脖子鹿。

输入输出格式

输入格式：

输入的第一行为两个正整数N，M，K。其中K表示禁止放置长脖子鹿的格子数。

第22~第K+1行每一行为两个整数 Xi, Yi表示禁止放置的格子。

输出格式：

一行一个正整数，表示最多能放置的长脖子鹿个数。

代码

二分图的最大独立集，我们考虑如何进行黑白染色。

如果我们按点来进行二分图建立的话，那么发现黑点都连黑点，白点都连白点。所以这样做一定是错的。

那么我们按行来进行黑白染色的话，这样就好了。

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=300+5,maxm=800000+100;
int head[maxn*maxn],dis[maxn*maxn];
int cur[maxn*maxn];
bool mark[maxn][maxn];
int n,m,k;
int s,t;
struct egde
{
	int to,next,cap;
}e[maxm];
int size=1;
int dx[]={1,1,-1,-1,3,3,-3,-3},dy[]={3,-3,3,-3,1,-1,1,-1};
void addedge(int u,int v,int val)
{
	e[++size].to=v;e[size].cap=val;e[size].next=head[u];head[u]=size;
	e[++size].to=u;e[size].cap=0;e[size].next=head[v];head[v]=size;
}
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch<='9'&&ch>='0'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*f;
}
bool bfs()
{
	memset(dis,0,sizeof(dis));
	deque<int>q;
	q.push_back(s);
	dis[s]=1;
	while(!q.empty())
	{
		int u=q.front();
		q.pop_front();
		for(int i=head[u];i;i=e[i].next)
		{
			int to=e[i].to;
			if(!dis[to]&&e[i].cap>0)
			{
				dis[to]=dis[u]+1;
				if(q.empty()||dis[to]>dis[q.front()])q.push_back(to);
				else q.push_front(to);
			}
		}
	}
	return dis[t];
}
int dinic(int u,int f)
{
	if(u==t)return f;
	for(int &i=cur[u];i;i=e[i].next)
	{
		int to=e[i].to;
		if(dis[to]==dis[u]+1&&e[i].cap>0)
		{
			int d=dinic(to,min(f,e[i].cap));
			if(d>0)
			{
				e[i].cap-=d;
				e[i^1].cap+=d;
				return d;
			}
    	}
	}
	return 0;
}
int maxflow()
{
	int flow=0;
	while(bfs())
	{
		memcpy(cur,head,sizeof(head));
		while(1)
		{
			int f=dinic(s,inf);
			if(f==0)break;
			flow+=f;
		}
	}
	return flow;
}
int id(int i,int j)
{
	return (i-1)*m+j;
}
int main()
{
	n=read(),m=read(),k=read();
	s=0,t=n*m+1;
	for(int i=1;i<=k;i++)
	mark[read()][read()]=1;
	for(int i=1;i<=n;i++)
	  for(int j=1;j<=m;j++)
	  {
	  	if(mark[i][j])continue;
	  	int u=id(i,j);
	  	if(i&1)
	  	{
	  		addedge(s,u,1);
            for(int l=0;l<8;l++)
            {
            	int x=i+dx[l],y=j+dy[l];

            	if(mark[x][y])continue;
            	if(x<1||x>n||y<1||y>m)continue;
            	int v=id(x,y);
            	addedge(u,v,1);
			}
		}
		else addedge(u,t,1);
	  }

	printf("%d",n*m-k-maxflow());
	return 0;
}