3D Computer Grapihcs Using OpenGL - 14 OpenGL Instancing
如果我们需要绘制两个(或者多个)一样的立方体(或者物体),只是位置、缩放、旋转不一样,那么我们可以不需要多次将这个物体的顶点信息、颜色信息等发送到显卡,而是发送一次,绘制多次,仅仅是每次绘制之前应用不同的转换矩阵。这种方法叫做OpenGL Instancing。它的效率比每次都重新发送一次数据到显卡要高很多。
看具体代码:
void MyGlWindow::paintGL()
{
glClear(GL_DEPTH_BUFFER_BIT | GL_COLOR_BUFFER_BIT);
glViewport(, , width(), height()); //cube1
glm::mat4 projectionMatrix = glm::perspective(30.0f, ((float)width()) / height(), 0.1f, 10.0f);
glm::mat4 translationMatrix = glm::translate(projectionMatrix, glm::vec3(0.0f, 0.0f,-3.0f));
glm::mat4 fullTransformMatrix = glm::rotate(translationMatrix, 54.0f, glm::vec3(1.0f, 0.0f, 0.0f)); GLint fullTransformMatrixUniformLocation = glGetUniformLocation(programID, "fullTransformMatrix");
glUniformMatrix4fv(fullTransformMatrixUniformLocation, , GL_FALSE, &fullTransformMatrix[][]);
glDrawElements(GL_TRIANGLES, numIndices, GL_UNSIGNED_SHORT, ); //cube2
translationMatrix = glm::translate(projectionMatrix, glm::vec3(2.0f, 0.0f, -4.0f));
fullTransformMatrix = glm::rotate(translationMatrix, 126.0f, glm::vec3(0.0f, 1.0f, 0.0f));
glUniformMatrix4fv(fullTransformMatrixUniformLocation, , GL_FALSE, &fullTransformMatrix[][]);
glDrawElements(GL_TRIANGLES, numIndices, GL_UNSIGNED_SHORT, ); }
我们仅在paintGL()函数中增加了几行代码(16-19行),就可以绘制另外一个立方体。
我们在16-17行重新改变了translationMatrix和fullTransformMatrix转换矩阵(我们甚至都没有定义新的矩阵,而仅仅是改变其数值),重新改变了位置、旋转。projection 矩阵我们并不想改变,还是之前的设置。
第18行和12行完全一样,但是这是必须的,因为要重新应用这个uniform变量才能起作用。
第19行使用了新的变换矩阵对立方体进行了第二次绘制。编译运行我们得到以下效果:
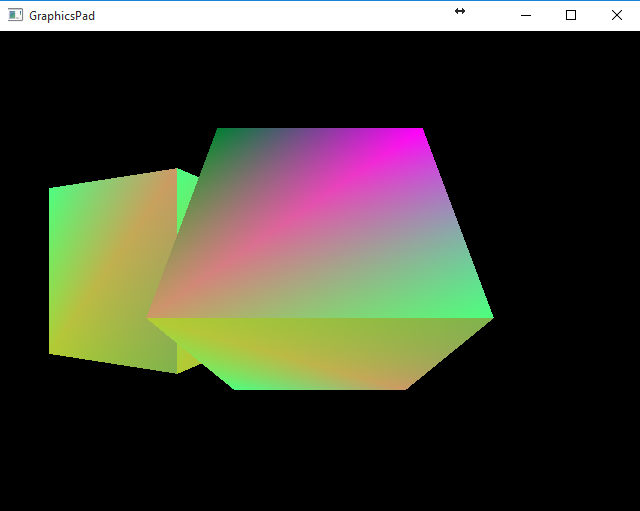
3D Computer Grapihcs Using OpenGL - 14 OpenGL Instancing的更多相关文章
- 3D Computer Grapihcs Using OpenGL - 15 Draw Element Instanced
友情提示:继续本节之前,需要保存此前的代码,本节为了试验,会对代码做一些修改,但后续的修改需要我们把代码返回之前的进度. OpenGL内置支持Instancing,有专门的函数来处理这件事情. 为了方 ...
- 3D Computer Grapihcs Using OpenGL - 16 使用DrawElementsInstanced绘制立方体
我们使用15节学到的知识来绘制14节的立方体. 在第14节我们使用了两次glDrawElements实现了OpenGL实例化,发现这样仍然不太方便,如果需要绘制成千上万的立方体,就需要手写成千上万次的 ...
- 3D Computer Grapihcs Using OpenGL - 19 Vertex Array Object(顶点数组对象)
大部分OpenGL教程都会在一开始就讲解VAO,但是该教程的作者认为这是很不合理的,因为要理解它的作用需要建立在我们此前学过的知识基础上.因此直到教程已经进行了一大半,作者才引入VAO这个概念.在我看 ...
- 3D Computer Grapihcs Using OpenGL - 09 Enable Depth Test
启用Depth Test OpenGL是个3D绘图API,也就是说不只有xy坐标轴,还有第三个坐标轴z,z轴的方向是垂直于屏幕,指向屏幕内. 靠近人眼的方向是负方向,标准化设备坐标的最小值是-1, 最 ...
- 3D Computer Grapihcs Using OpenGL - 06 Vertex and Fragment Shaders
从这里就接触到了可编程图形渲染管线. 下面介绍使用Vertex Shader (顶点着色器)和 Fragment Shader(像素着色器)的方法. 我们的目标是使用这两个着色器给三角形填充绿色. 添 ...
- 3D Computer Grapihcs Using OpenGL - 03 OpenGL Buffer Data
本节绘制一个三角形,并讲解Buffer Object-缓冲对象 OpenGL的窗口坐标 屏幕中心为坐标原点,横向朝右为x正方向,纵向朝上为y正方向,最大值最小值分别为1,-1. Buffer Obje ...
- 3D Computer Grapihcs Using OpenGL - 10 Color Buffer
本节我们将尝试利用三角形制作一个“走马灯”效果. 一个三角形如图示方式,从左向右依次移动. 先看一下代码: MyGlWindow.cpp #include <gl\glew.h> #inc ...
- 3D Computer Grapihcs Using OpenGL - 05 EBO
本节将采用两种方法绘制两个三角形. 先看第一种方法的代码 MyGlWindow.cpp #include <gl\glew.h> #include "MyGlWindow.h&q ...
- 3D Computer Grapihcs Using OpenGL - 04 First Triangle
本节将绘制一个三角形 先看最终代码: MyGlWindow.cpp: #include <gl\glew.h> #include "MyGlWindow.h" void ...
随机推荐
- [转帖]vCenter 计划任务.
vSphere5.0实用小技巧-DPM计划任务 2013年05月12日 23:00:09 weixin_34185320 阅读数:9 https://blog.csdn.net/weixin_3418 ...
- [转帖]VMWare官网:无法关闭 ESXi 主机上的虚拟机 (1014165)
无法关闭 ESXi 主机上的虚拟机 (1014165) https://kb.vmware.com/s/article/1014165?lang=zh_CN Last Updated: 4/17/20 ...
- Office批量授权(VL)版本和激活方法
Office 2010 Office 2010中文专业增强版 32位 文件名: SW_DVD5_Office_Professional_Plus_2010w_SP1_W32_ChnSimp_CORE_ ...
- php多域名单站点路由
能够使多域名但是只有一个站点的小站,通过路由访问到各个指定目录 <?php //域名跳转路由 //默认跳转 $default = "http://www.stanwind.com/in ...
- 06、CEL文件与灰度图像
R语言里的image方法可以绘制CEL文件的灰度图像.我们先来讨论image这个的函数: 如:x <- c(0:2) y <- c(0:2) m <- matrix(c(1,5,10 ...
- orm的设计思路
一,我们先搞懂什么是orm? ORM:对象关系映射(Object Relational Mapping,简称ORM),目的是想像操作对象一样操作数据库.因为数据库不是面向对象的,所以需要编程进行映射. ...
- 微信小程序实现滑动删除效果
在一些app中,随处可见左滑动的效果,在微信小程序中,官方并未提供相关组件,需要我们自己动手写一个类似的效果 下面仅列举出核心代码,具体的优化需要根据你自身的需求 <view class='li ...
- 曹工说Spring Boot源码(5)-- 怎么从properties文件读取bean
写在前面的话 相关背景及资源: 曹工说Spring Boot源码(1)-- Bean Definition到底是什么,附spring思维导图分享 曹工说Spring Boot源码(2)-- Bean ...
- EL作用域对象
EL与jsp的作用域对象对应关系,,,,,及EL具体作用域对象介绍,如下
- 利用logrotate切割nginx的access.log日志
一.新建一个nginx的logrotate配置文件 /var/log/nginx/access.log { daily rotate compress delaycompress missingok ...
