【CF 463F】Escape Through Leaf

题意

　　给你一棵 \(n\) 个点的树，每个节点有两个权值 \(a_i,b_i\)。

　　从一个点 \(u\) 可以跳到以其为根的子树内的任意一点 \(v\)（不能跳到 \(u\) 自己），代价是 \(a_u\times b_v\)。

　　求每个点跳到任意一个叶子的最小代价。

　　\(n\le 10^5, -10^5\le a_i,b_i\le 10^5\)

题解

暴力

　　考虑暴力 \(dp\)，设 \(dp_i\) 表示从叶子跳到 \(i\) 号点的最小代价。

　　则有转移 \(dp_u = \min\{a_u\times b_v + dp_v\}\)

　　复杂度 \(O(n^2)\)

优化

　　发现这是一个裸的斜率优化式子，转移为求多条直线 \(y=kx+b\) 在直线 \(x=a_u\) 处的最值（\(k=b_v, b=dp_v\)）

　　好像就是需要维护一个支持动态插入直线的上凸包？是不是写个支持合并的凸包平衡树就行了？

　　平衡树合并的方法就是启发式合并，把两个 splay 中小的 splay 里面的所有点暴力插入大的 splay。每个点被暴力重新插入后 其所在的 splay 至少增大一倍，所以最多被插入 \(\log n\) 次，一次插入的复杂度最大是 \(O(\log n)\)，总时间复杂度就是 \(O(n \log^2 n)\)。

　　综上，可以写平衡树合并来通过此题，但是 CF 这场比赛 \(2\) 小时让你打 \(7\) 道题，你写这鬼玩意所需的时间肯定不止 \(2\) 小时……

　　观察发现，我们只需要查询 \(x=a_u\) 处的最值，这个操作好像可以用李超树维护？

　　于是我们只需要写个支持合并的李超树……

　　李超树合并与平衡树同理（但是代码量短多了），用启发式合并，把两个李超树中 小的李超树里面的所有点 暴力插入大的李超树，时间复杂度与平衡树合并的复杂度差不多，都是 \(O(n\log^2 n)\)。

　　代码好写就够了。

---

　　upd：今天下午被这么一个问题搞自闭了

　　因为有些线段树相关的题的空间是 \(O(n\log n)\) 甚至 \(O(n\log^2 n)\) 的，而动态开点实际上不会开很多点，所以你可能会适当减少线段树数组的大小。然而因为你少开空间有可能被卡，所以你可能会在本地尝试卡空间。这样做并不保险，你可能本机开了空间上限 \(-10MB\)，但交上去不排除因为测评环境不同而 MLE 的可能，也就是说控制不当你就有爆 \(0\) 的风险。

　　为了避免这种风险，我以前有一个用 vector 代替动态开点线段树数组的想法，这样你不但不用手算空间，甚至运行时间都会少一大截。

　　然后我对这题测试了一波，发现当 \(n\) 达到 \(1w\) 出头时就开始 RE 了……

　　更惊人的是 CF 竟然没有给出 RE 的错误原因（注意上面那个 RE 提交）

　　

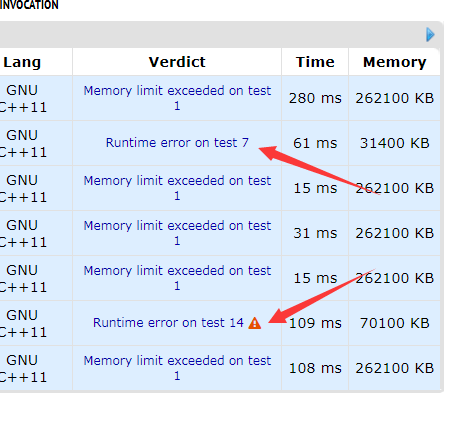
　　zbl

　　在本机面向数据和程序二分了一波，发现跑到 \(\text{ins}\) 函数时炸了

#define ls tr[o].l
#define rs tr[o].r
struct Tree{
    line v; int l,r,siz;
    Tree(){v=line(); l=r=0, siz=1;}
};
vector<Tree> tr;
void ins(int &o, int l, int r, line v){
    if(!o) o=++cnt, tr.push_back(Tree());
    int mid=l+r>>1;
    if(cmp(tr[o].v, v, mid)) swap(tr[o].v,v);
    if(l==r || tr[o].v.k==v.k || !v.id) return;

    double x = cross(tr[o].v,v);
    if(x<l || x>r) return;
    if(v.k > tr[o].v.k) ins(ls,l,mid,v);
    else ins(rs,mid+1,r,v);
    pushup(o);
}

　　经过调试，发现 vector \(\text{pushback}\) 到第 \(8192\) 位后，\(o\) 这个变量炸了（一输出它就 RE，一用它就 RE，把输出换成其它变量或字符串都能正常输出）

　　我就不是很懂了，\(o\) 这个变量到底是咋了？

　　然后为了输出 \(o\) 这个变量调了一下午未果，请了很多人也没能解决

　　有个大佬还主动用 linux 帮我输出 pdb 内部给的错误信息，然而得到的错误信息只有“堆空间删除后再利用”，其它的报错根本不明意义

　　后来群里还有个人私聊我，说他以前用 vector 开线段树数组也因为这个问题 RE 了，一直没有解决。当时我以为开发者把 c++ STL 写锅了

　　熬到晚上，有个福州一中的神爷给出了解释？！

　　vector 是倍增式开空间，即当它 \(\text{pushback}\) 到 \(2^n（n∈Z）\) 时，它会申请一个新的长度为 \(2^{n+1}\) 的空间，也就是把整个 vector 的地址平移了。

　　vector 的地址平移会使你目前有关这个 vector 的指针全部失效，因为你的指针指向的是 vector 平移前的地址，现在 vector 已经移走了，你的指针就指空了，输出这个位置就炸了（即堆空间删除后再利用，因为地址本身可能与堆有关）。观察 \(o\) 这个引用指针指向了谁——发现就是 \(ls,rs\)，即 \(tr[o].l,tr[o].r\)，而 tr 这个 vector 在 \(\text{pushback}\) 到第 \(8192\) 位后就平移了，所以 \(o\) 这个指针指的地址没了。

　　换成数学用语就是说：\(tr\) 是一个 vector，设平移前 \(tr\) 的起点是一个地址 \(a\)，\(o=tr[x].l\) 就相当于 \((a+x)->l\)。\(tr\) 平移后 \(tr[o].l\) 变成了 \((a'+x)->l\)，但你的 \(o\) 指针指向的地址还是 \((a+x)->l\)。

　　所以对 vector 要慎用指针之类的东西，防止 vector 地址平移导致指针失效。

　　看起来大功告成了？

　　还没完，我改成这么写还是炸：

#define ls tr[o].l
#define rs tr[o].r
struct Tree{
    line v; int l,r,siz;
    Tree(){v=line(); l=r=0, siz=1;}
};
vector<Tree> tr;
int ins(int o, int l, int r, line v){
    if(!o) o=++cnt, tr.pb(Tree());
    int mid=l+r>>1;
    if(cmp(tr[o].v, v, mid)) swap(tr[o].v,v);
    if(l==r || tr[o].v.k==v.k || !v.id) return o;

    double x = cross(tr[o].v,v);
    if(x<l || x>r) return o;
    if(v.k > tr[o].v.k) ls = ins(ls,l,mid,v);
    else rs = ins(rs,mid+1,r,v);
    pushup(o);
    return o;
}

　　炸的地方没变，还是开到第 \(8192\) 位就炸了

　　然后我就开始喷：wcnm 这软件绝对写挂了

　　冷静分析，发现问题可能出在这：

if(v.k > tr[o].v.k) ls = ins(ls,l,mid,v);
else rs = ins(rs,mid+1,r,v);

　　有可能是赋值时先取了左边变量的地址，然后再计算右边变量，再赋到左边变量的地址上。这样的话，先前取的 \(ls/rs\) 的地址在赋值时还是指空了，所以大胆猜测这是炸的原因。

　　解决方法很显然，用一个变量暂存返回值，再赋给 \(ls/rs\) 即可。具体见下方代码。

　　总而言之就是 STL 的写法是真奇怪，经常在内存地址等各种难懂的地方出问题，用户体验不是很好。建议慎用 STL，考前一定要了解使用 STL 可能出现的各种 CE/RE 情况。

　　不过用 vector 代替数组挺好的，看看测试结果就知道啦：

　　\(500w\) 位数组开线段树

　　vector 开线段树

---

#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define N 100005
#define lim 100001
#define Lim 200003
const ll inf = 1ll<<60;
using namespace std;
inline int read(){
	int x=0; bool f=1; char c=getchar();
	for(;!isdigit(c); c=getchar()) if(c=='-') f=0;
	for(; isdigit(c); c=getchar()) x=(x<<3)+(x<<1)+(c^'0');
	if(f) return x;
	return 0-x;
}
int n,a[N],b[N];
ll dp[N];
vector<int> g[N];
struct line{
	int k; ll b;
	bool id;
	line(){k=0, b=0, id=0;}
	line(int _k, ll _b, bool _id){k=_k, b=_b, id=_id;}
	ll getY(int x){return (ll)k*x+b;}
};
inline bool cmp(line a, line b, int x){
	if(!a.id) return 1;
	return a.getY(x)>b.getY(x);
}
inline double cross(line a, line b){
	return (double)(a.b-b.b)/(b.k-a.k);
}
int rt[N];
struct LiChaoTree{
	#define ls tr[o].l
	#define rs tr[o].r
	struct Tree{
		line v; int l,r,siz;
		Tree(){v=line(); l=r=0, siz=1;}
	};
	vector<Tree> tr;
	int cnt;
	inline void pushup(int o){
		tr[o].siz = tr[ls].siz + tr[rs].siz + 1;
	}
	int ins(int o, int l, int r, line v){
		if(!o) o=++cnt, tr.pb(Tree());
		int mid=l+r>>1;
		if(cmp(tr[o].v, v, mid)) swap(tr[o].v,v);
		if(l==r || tr[o].v.k==v.k || !v.id) return o;

		double x = cross(tr[o].v,v);
		if(x<l || x>r) return o;
		if(v.k > tr[o].v.k){
			int wtf = ins(ls,l,mid,v);
			ls=wtf;
		}
		else{
			int wtf = ins(rs,mid+1,r,v);
			rs=wtf;
		}
		pushup(o);
		return o;
	}
	int merge(int x, int y, int l, int r){
		if(!x || !y) return x|y;
		ins(x,l,r,tr[y].v);
		int mid=l+r>>1;
		int wtf = merge(tr[x].l, tr[y].l, l, mid);   tr[x].l=wtf;
			wtf = merge(tr[x].r, tr[y].r, mid+1, r); tr[x].r=wtf;
		pushup(x);
		return x;
	}
	inline int merge(int x, int y){
		if(tr[x].siz<tr[y].siz) swap(x,y);
		return merge(x,y,1,Lim);
	}
	ll query(int o, int l, int r, int x){
		if(l==r) return tr[o].v.id ? tr[o].v.getY(x) : inf;
		int mid=l+r>>1; ll ret;
		if(x<=mid){
			if(!ls) return tr[o].v.getY(x);
			ret=query(ls,l,mid,x);
		}
		else{
			if(!rs) return tr[o].v.getY(x);
			ret=query(rs,mid+1,r,x);
		}
		return tr[o].v.id ? min(ret, tr[o].v.getY(x)) : ret;
	}
	#undef ls
	#undef rs
}sgt;
inline void ins(int x){
	int k=b[x]; ll b=dp[x]-(ll)lim*k;
	rt[x] = sgt.ins(rt[x], 1, Lim, line(k,b,1));
}
inline ll query(int x){
	return sgt.query(rt[x], 1, Lim, a[x]+lim);
}
void dfs(int u, int fa){
	bool flag=0;
	for(int i=0; i<g[u].size(); ++i){
		int v=g[u][i];
		if(v==fa) continue;
		flag=1;
		dfs(v,u);
		rt[u] = sgt.merge(rt[u], rt[v]);
	}
	if(flag) dp[u] = query(u);
	ins(u);
}
int main(){
	//freopen("1.in","r",stdin);
	//freopen("1.out","w",stdout);
	sgt.tr.pb(LiChaoTree::Tree());
	n=read();
	for(int i=1; i<=n; ++i) a[i]=read();
	for(int i=1; i<=n; ++i) b[i]=read();
	int u,v;
	for(int i=1; i<n; ++i){
		u=read(), v=read();
		g[u].pb(v), g[v].pb(u);
	}
	dfs(1,0);
	for(int i=1; i<=n; ++i) printf("%lld ",dp[i]);
	return 0;
}

　　总结一点：不少斜率优化题都是单点求最值，所以可以用李超树这个简单的数据结构维护。但李超树并不能动态维护凸包面积，所以像【HAOI2011 防线修建】这种题就只能用平衡树做。