【算法】Normalization

Normalization（归一化）

写这一篇的原因是以前只知道一个Batch Normalization，自以为懂了。结果最近看文章，又发现一个Layer Normalization，一下就懵逼了。搞不懂这两者的区别。后来是不查不知道，一查吓一跳，Normalization的方法五花八门，Batch Normalization, Layer Normalization, Weight Normalization, Cosine Normalization, Instance Normalization, Group Normlization, Switchable Normlization.... 估计我没看到的还有很多。而且郁闷的是，感觉越看越不懂了...

这里简单记录一下目前的理解与问题。

白化

白化的目的是希望特征符合独立同分布i.i.d条件。包括:

1. 去除特征之间的相关性 —> 独立；
2. 使得所有特征具有相同的均值和方差 —> 同分布。

这里我有了第一个问题。什么叫做去除特征之间的相关性?
比如，有两个输入向量，X1=(x11,x12,x13,x14), X2=(x21,x22,x23,x24)
去除特征之间的相关性，只是去除x11,x12,x13,x14之间的相关性，还是去除x11和x21的相关性？

Normalization的好处

1. 使得数据更加符合独立同分布条件，减少internal corvariate shift导致的偏移
2. 使数据远离激活函数的饱和区，加快速度。(我理解是只对sigmoid这样的激活函数有效，对relu则没有加速作用了)

Normalization基本公式

\[h=f(g\frac{x-\mu}{\sigma}+b)\]

\(\mu\):均值
\(\sigma\):方差根
\(b\): 再平移参数，新数据以\(b\)为均值
\(g\): 再缩放参数，新数据以\(g^2\)为方差
归一化后的目标就是统一不同\(x\)之间的均值和方差

加入\(g\)和\(b\)的目的是使数据一定程度偏离激活函数的线性区，提高模型表达能力。因为均值是0的话正好落在sigmoid函数的线性部分。

第二个问题，g和b是根据什么确定的，是trainable的吗？

Batch Normalization

Batch Normalization是针对不同batch导致的数据偏移做归一化的方式。比如，一个batch有3个输入，每个输入是一个长度为4的向量。
\(X1=(x11,x12,x13,x14)\)
\(X2=(x21,x22,x23,x24)\)
\(X3=(x31,x32,x33,x34)\)

在上述条件下，归一化时的均值是：
\(\mu=(\frac{x11+x21+x31}{3},\frac{x12+x22+x32}{3},\frac{x13+x23+x33}{3},\frac{x14+x24+x34}{3})\)

这里主要展示一下计算时的方向，即对于每个元素位置，对不同的输入做归一化。方差同理。

第三个问题，很多文章都说batch norm需要在batch size较大，不同batch之间均值方差相差不大的情况下效果好。
即batch的均值方差跟整体的均值方差一致时效果好。
这我就不懂了，无论之前每个batch的分布是怎样的，经过归一化，都已经是相同分布了。为什么一定要原始batch之间分布相似呢？

Batch norm有个缺点，即需要记录每一个batch输入的均值和方差，对于变长的RNN网络来说计算麻烦。

第四个问题：为什么要记录每个batch的均值和方差？对RNN效果不好仅仅因为麻烦吗？
我个人理解BN在RNN上效果不好的原因是，虽然RNN训练时网络深度很深，但实际上只有一个神经元节点，相当于把所有层的神经元的均值和方差设定为相同的值了，导致效果不佳。

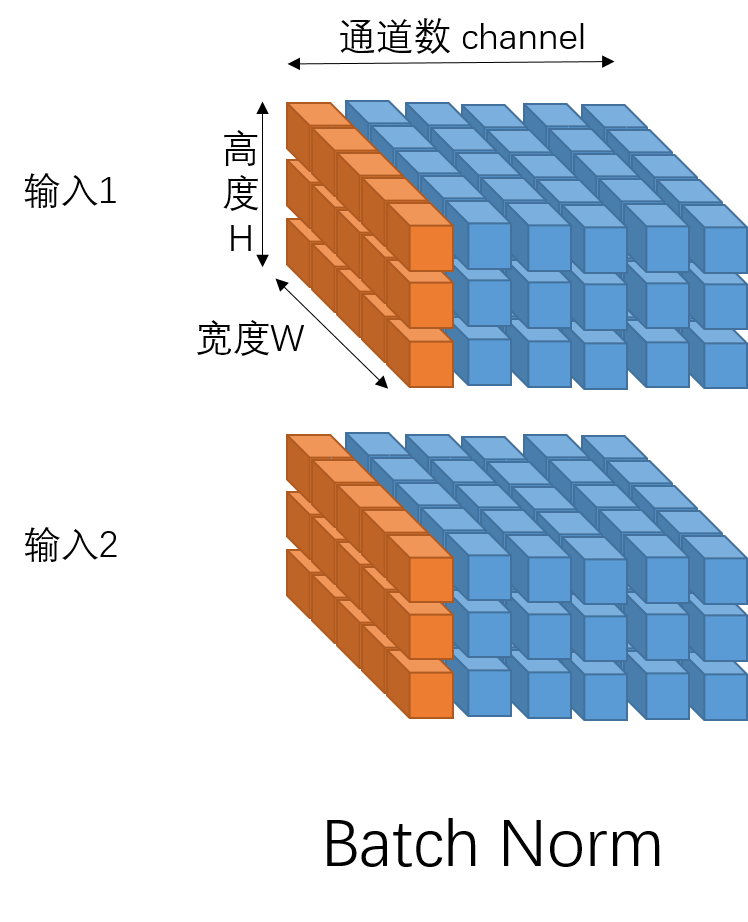
如果是图像，则输入是一个四维矩阵，(batch_size, channel_size, weight, height),此时batch norm是针对同一个batch的不同输入中属于同一通道的元素做归一化。如下图，是一个batch_size=2, channel_size=6, weight=5, height=3的例子。一次batch norm是对所有橙色部分元素做归一化。

Layer Normalization

Layer Normalization是针对同一个输入的不同维度特征的归一化方式。还是用上面的例子。
对于\(X1\)来说，layer norm的归一化均值是： \(\mu=\frac{x11+x12+x13+x14}{4}\)

对于图像来说，则是对一个输入的所有元素做归一化。如下图橙色部分：

Instance Norm

对一个输入图像的一个通道中的所有元素做归一化。如下图橙色部分：

Group Norm

对于一个输入图像的多个通道元素做归一化。如下图橙色部分:

Weight Norm

前面的归一化方法都是从不同维度对输入数据做归一化，而weight norm则是对权重做归一化。

Cosine Norm

抛弃了权重和输入点积的计算方式，改用其他函数。

参考文献

1. https://zhuanlan.zhihu.com/p/33173246
2. https://blog.csdn.net/liuxiao214/article/details/81037416