轻量化模型系列--GhostNet：廉价操作生成更多特征

前言

由于内存和计算资源有限，在嵌入式设备上部署卷积神经网络 (CNN) 很困难。特征图中的冗余是那些成功的 CNN 的一个重要特征，但在神经架构设计中很少被研究。

论文提出了一种新颖的 Ghost 模块，可以从廉价操作中生成更多的特征图。提出的 Ghost 模块可以作为即插即用的组件来升级现有的卷积神经网络。堆叠Ghost Module建立了轻量级的 GhostNet。

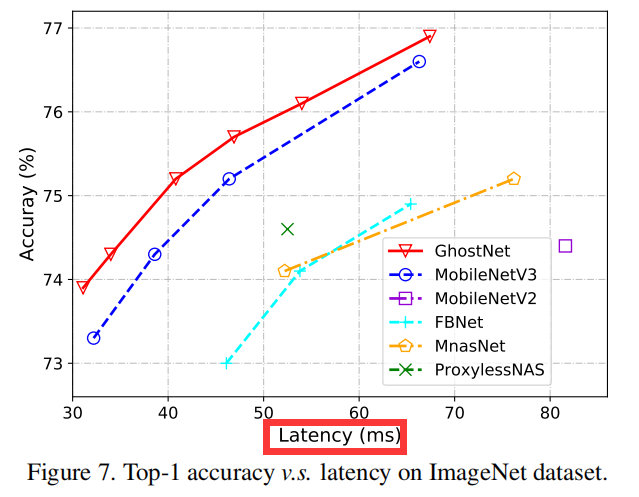
GhostNet 可以实现比 MobileNetV3 更高的识别性能（例如 75.7% 的 top-1 准确率），并且在 ImageNet ILSVRC-2012 上具有相似的计算成本。

论文：GhostNet: More Features from Cheap Operations

代码：https://github.com/huawei-noah/ghostnet.

欢迎关注公众号 CV技术指南，专注于计算机视觉的技术总结、最新技术跟踪、经典论文解读。

出发点

多年来，已经提出了一系列方法来研究紧凑型深度神经网络，例如网络剪枝、低位量化、知识蒸馏等。网络剪枝修剪神经网络中不重要的权重、利用正则化来修剪过滤器以获得高效的 CNN；低位量化将权重和激活量化为 1 位数据，以实现大的压缩和加速比；知识蒸馏，将知识边缘从较大的模型转移到较小的模型。

然而，这些方法的性能通常受预训练的神经网络作为其基线的上限。

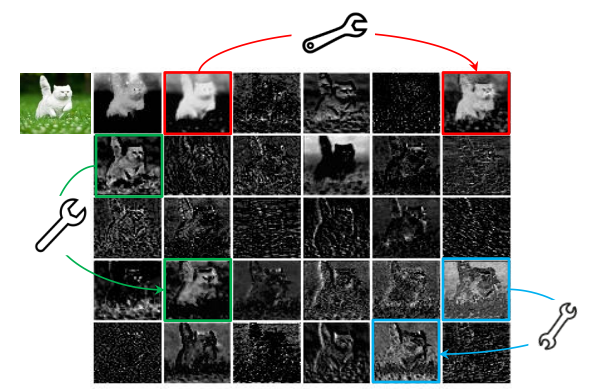
训练好的深度神经网络的特征图中的丰富甚至冗余信息通常可以保证对输入数据的全面理解。例如，上图展示了 ResNet-50 生成的输入图像的一些特征图，并且存在许多相似的特征图对，就像彼此的幽灵。特征图中的冗余可能是成功的深度神经网络的一个重要特征。我们倾向于采用它们，而不是避免冗余的特征图，但以一种具有成本低的方式。

这里补充一句：一个训好的正常大小的网络中，存在大量的冗余特征图，模型剪枝(或模型压缩)、正则化属于减少冗余特征图的方式，而这篇论文认为这些冗余信息会对于正确识别或检测具有重要的作用。

推荐阅读《我们真的需要模型压缩吗》更好理解上面这段话。

主要贡献

引入了一个新的 Ghost 模块，通过使用更少的参数来生成更多的特征。 具体来说，深度神经网络中的一个普通卷积层会被分成两部分。第一部分涉及普通卷积，但它们的总数将受到严格控制。给定第一部分的内在特征图，然后应用一系列简单的线性操作来生成更多的特征图。在不改变输出特征图的大小的情况下，与普通卷积神经网络相比，这个 Ghost 模块所需的总体参数数量和计算复杂度有所降低。

基于 Ghost 模块，建立了一个高效的神经架构，即 GhostNet。 首先替换基准神经架构中的原始卷积层以证明 Ghost 模块的有效性，然后验证 GhostNets 在几个基准视觉数据集上的优越性。

实验结果表明，所提出的 Ghost 模块能够降低通用卷积层的计算成本，同时保持相似的识别性能，并且 GhostNets 可以在各种任务上超越SOTA高效深度模型，如 MobileNetV3 移动设备上的快速推理。

Methods

Ghost module

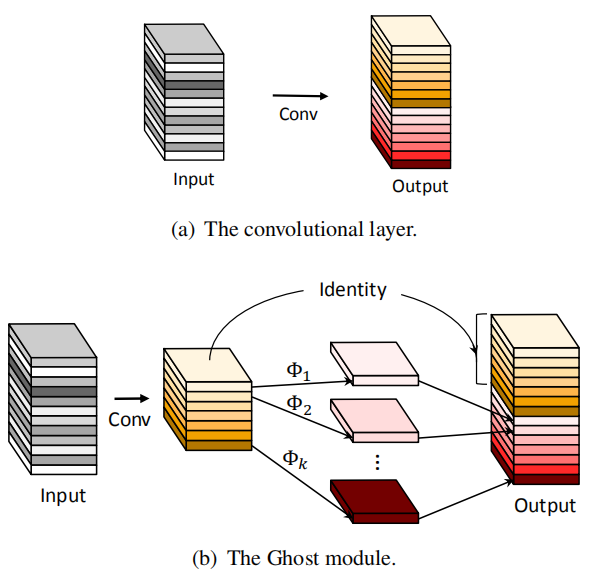
如上图所示，Ghost module先通过正常卷积，将input通道数减少，再通过一个depthwise卷积和identity(恒等变换)。

1. 前面的卷积既可以使用1x1卷积，也可以使用正常的3x3或5x5卷积。

2. 这里的Φ即为cheap operation，既可以是depthwise卷积，也可以是其它方式的卷积，例如分组卷积。这部分的作用就是生成了相似特征图。也就是前面说的，用成本更低的方式，保留了那些冗余信息。

3. 恒等映射与 Ghost 模块中的线性变换并行以保留内在特征映射。

复杂度分析

假设我们输入特征图的尺寸是h*w*c,输出特征图的尺寸是h’*w’*n,卷积核大小为k*k。

在cheap operation变换中，我们假设特征图的channel是m，变换的数量是s，最终得到的新的特征图的数量是n,那么我们可以得到等式：

n = m ∗ s

由于Ghost的变换过程中最后存在一个恒等变换（Identity），所以实际有效的变换数量是s-1,所以上式可以得到如下公式：

m ∗ ( s − 1 ) = n / s ∗ ( s − 1 )

所以，理论的速度比为：

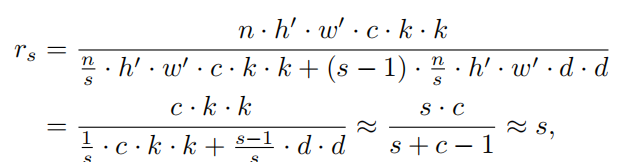
理论的压缩比为：

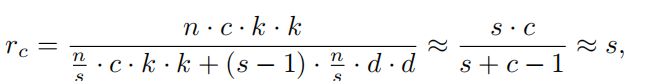
其中，s远小于c。

GhostNet

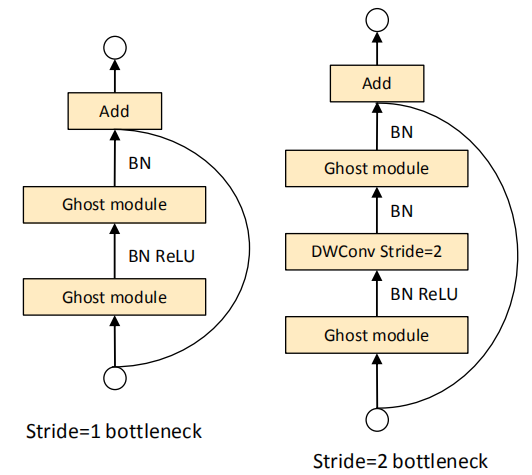
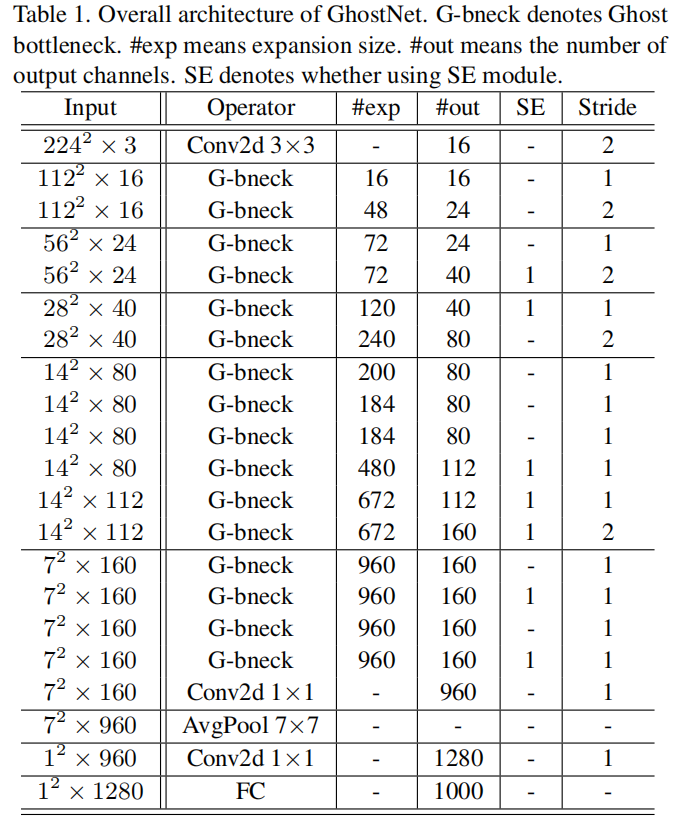
Conclusion

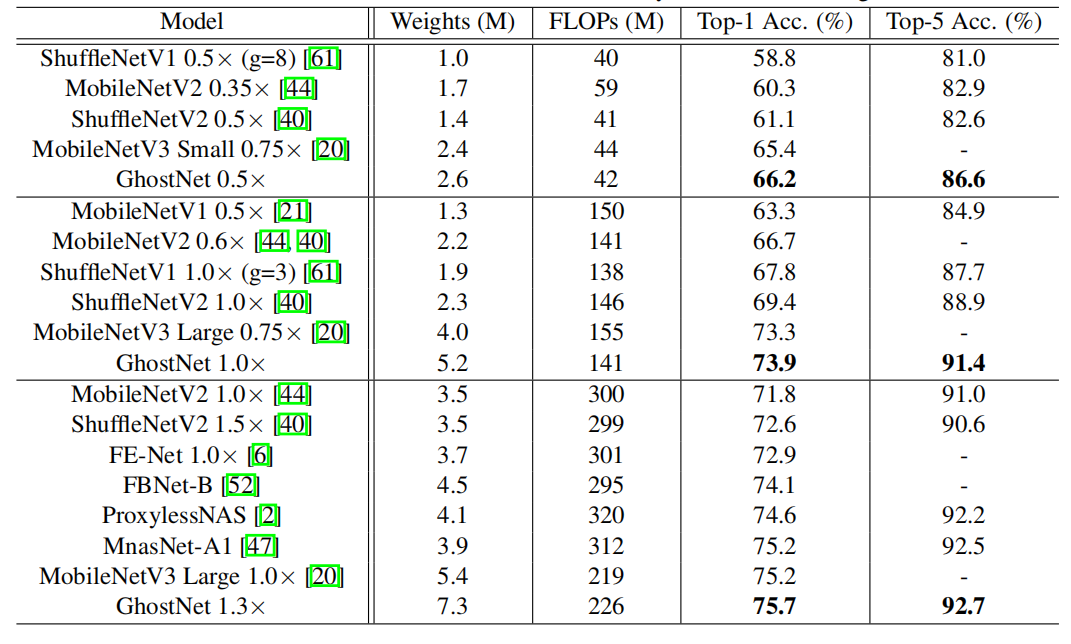
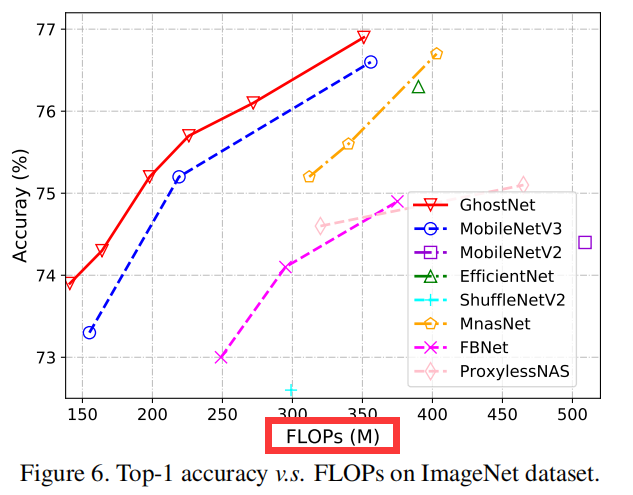
本文来源于公众号 CV技术指南的论文分享系列。

欢迎关注公众号 CV技术指南，专注于计算机视觉的技术总结、最新技术跟踪、经典论文解读。

在公众号中回复关键字 “技术总结”可获取公众号原创技术总结文章的汇总pdf。

其它文章

CV技术指南--精华文章汇总分类

神经网络超参数的调参方法总结

轻量化模型系列--GhostNet：廉价操作生成更多特征

ICCV2021 | MicroNet：以极低的 FLOPs 改进图像识别

CVPR2021 | 重新思考BatchNorm中的Batch

ICCV2021 | 重新思考视觉transformers的空间维度

CVPR2021 | Transformer用于End-to-End视频实例分割

ICCV2021 |(腾讯优图)重新思考人群中的计数和定位：一个纯粹基于点的框架

经典论文系列--胶囊网络：新的深度学习网络

经典论文系列 | 目标检测--CornerNet & 又名 anchor boxes的缺陷

如何看待人工智能的泡沫

使用Dice loss实现清晰的边界检测

PVT--无卷积密集预测的多功能backbone

CVPR2021 | 开放世界的目标检测

Siamese network总结

视觉目标检测和识别之过去，现在及可能

在做算法工程师的道路上，你掌握了什么概念或技术使你感觉自我提升突飞猛进？

计算机视觉专业术语总结(一)构建计算机视觉的知识体系