【NOI2019集训题2】 序列 后缀树+splay+dfs序

题目大意：给你一个长度为$n$的序列$a_i$，还有一个数字$m$，有$q$次询问

每次给出一个$d$和$k$，问你对所有的$a_i$都在模$m$意义下加了$d$后，第$k$小的后缀的起点编号。

数据范围：$n≤100000，d≤a_i<m≤10^9，q≤5\times 10^5$

这一题我想的时候被最后一步卡主了（其实如果到那个时候估计也时间不够了）

我们不难找出一个单次询问$O(n)$的方法，我们每次暴力更新$a_i$，然后对原序列搞一棵后缀树出来，在上面暴力查询第$k$小即可。

如果没有加$d$的操作,只是单纯询问第k大的话，我们考虑对这棵后缀树按字典序先序遍历一遍，搞出dfs序，用平衡树维护这些点出现的先后顺序。

对于一次询问第$k$小，我们在平衡树上找出dfs序第$k$小的后缀节点出来，输出即可。

下面考虑加$d$的操作。

考虑到这一题并没有要求强制在线，我们考虑对所有的询问按$d$从小大到大排序。

随着d的增长，原先最大的数随着取模操作的发生，会变成最小的数。

也就是说会出现一个换位的情况

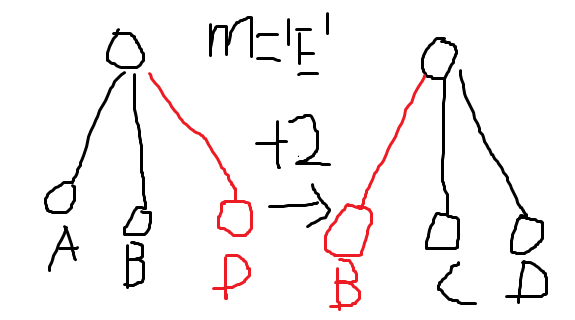
就像这样

显然这个红点下面还会接很多个节点，但是不管怎么换位，以红点为根的子树内孩子的数量是不会变的。

我们只需要不断地做搬动节点的操作（在平衡树中，取出一个区间，并把这个区间插入到另一个区间中），并且动态维护dfs序列即可。

在询问离线后，我们不难发现每个节点至多只需要被搬动一次。

那么时间复杂度就变成愉快的O((n+q)\ log\ n)了。

然而我在想的时候，并没有往dfs序上想，sam也不熟练

注意细节！

 #include<bits/stdc++.h>
 #define M 200005
 #define lc(x) ch[(x)][0]
 #define rc(x) ch[(x)][1]
 using namespace std;

 int dfn[M]={},low[M]={},t=; int n,m,q;

 namespace H{
     int ch[M][]={},fa[M]={},root,siz[M]={},psiz[M]={},p[M]={},rec[M]={},use=;

     void pushup(int x){siz[x]=siz[lc(x)]+siz[rc(x)]+;psiz[x]=psiz[lc(x)]+psiz[rc(x)]+p[x];}
     void rotate(int x,int &k){
         int y=fa[x],z=fa[y],l,r;
         l=(ch[y][]!=x); r=l^;
         if(y==k) k=x;
         else{
             if(ch[z][]==y) ch[z][]=x;
             else ch[z][]=x;
         }
         fa[x]=z; fa[y]=x; fa[ch[x][r]]=y;
         ch[y][l]=ch[x][r]; ch[x][r]=y;
         pushup(y); pushup(x);
     }
     inline void splay(int x,int &k){
         while(x!=k){
             int y=fa[x],z=fa[y];
             if(y!=k){
                 if((ch[y][]==x)^(ch[z][]==y)) rotate(x,k);
                 else rotate(y,k);
             }
             rotate(x,k);
         }
     }
     int build(int l,int r,int f){
         if(l>r) return ;
         int mid=(l+r)>>; fa[mid]=f;
         lc(mid)=build(l,mid-,mid);
         rc(mid)=build(mid+,r,mid);
         pushup(mid);
         return mid;
     }
     int find(int x,int k){
         if(siz[lc(x)]>=k) return find(lc(x),k);
         if(siz[lc(x)]+==k) return x;
         return find(rc(x),k-siz[lc(x)]-);
     }
     int findp(int x,int k){
         if(psiz[lc(x)]>=k) return findp(lc(x),k);
         if(psiz[lc(x)]+p[x]==k) return x;
         return findp(rc(x),k-psiz[lc(x)]-p[x]);
     }
     int getrank(int x){
         splay(x,root);
         return siz[lc(x)];
     }
     int split(int l,int r){
         int x=find(root,l),y=find(root,r+);
         splay(x,root); splay(y,ch[root][]);
         int res=lc(y);
         lc(y)=;
         splay(y,root);
         return res;
     }
     void ins(int k,int id){
         int x=find(root,k+);
         splay(x,root);
         int y=rc(x);
         while(lc(y)) y=lc(y);
         lc(y)=id; fa[id]=y;
         splay(lc(y),root);
     }
     void build(int nn){
         root=build(,nn+,);
         splay(,root);
         lc()=nn+; siz[]++; siz[nn+]++;
     }
 };

 int a[M]={};
 map<int,int> mp; vector<int> vt[M];

 namespace SAM{
     map<int,int> ch[M],son[M]; int l[M],fa[M],last=,use=,cnt=;
     int pos[M],ed[M],val[M],siz[M];
     void exc(int c,int id){
         int p=last,np=++use; l[np]=l[last]+; last=np;
         pos[np]=ed[np]=id;
         for(;p&&ch[p][c]==;p=fa[p]) ch[p][c]=np;
         if(!p) fa[np]=;
         else{
             int q=ch[p][c];
             if(l[p]+==l[q]) fa[np]=q;
             else{
                 int nq=++use;
                 l[nq]=l[p]+; fa[nq]=fa[q];
                 fa[q]=fa[np]=nq; ed[nq]=ed[q];
                 ch[nq]=ch[q];
                 for(int j=p;ch[j][c]==q;j=fa[j]) ch[j][c]=nq;
             }
         }
     }

     void build(){
         for(int i=n;i;i--)
         exc(a[i],i);
         for(int i=;i<=use;i++){
             val[i]=a[ed[i]+l[fa[i]]];
             if(mp[val[i]]==) mp[val[i]]=++cnt;
             vt[mp[val[i]]].push_back(i);
             son[fa[i]][val[i]]=i;
         }
     }

     void dfs(int x){
         dfn[x]=++t; siz[x]=;
         H::rec[t]=x;
         if(pos[x]) H::p[t]=;
         for(map<int,int>::iterator it=son[x].begin();it!=son[x].end();it++){
             dfs(it->second);
             siz[x]+=siz[it->second];
         }
         low[x]=t;
     }
     void updata(int ID){
         for(int i=;i<vt[ID].size();i++){
             int id=vt[ID][i];
             int F=fa[id];
             int wei=H::getrank(dfn[F]);
             int cutID=wei+siz[F]-siz[id];
             int P=H::split(cutID,cutID+siz[id]-);

             H::ins(wei,P);
         }
     }
 };

 struct ask{
     int d,k,id;
     ask(){d=k=id=;}
     void rd(int ID){id=ID; scanf("%d%d",&d,&k);}
     friend bool operator <(ask a,ask b){return a.d<b.d;}
 }Q[];

 int ans[]={};

 int main(){
 //    freopen("in.txt","r",stdin);
 //    freopen("out.txt","w",stdout);
     scanf("%d%d%d",&n,&m,&q);
     for(int i=;i<=n;i++) scanf("%d",a+i);

     SAM::build();
     SAM::dfs();
     H::build(SAM::use);

     for(int i=;i<=q;i++) Q[i].rd(i);
     sort(Q+,Q+q+);
     sort(a+,a+n+);
     int r=unique(a+,a+n+)-a-,cnt=r;

     for(int i=;i<=q;i++){
         while(r&&a[r]+Q[i].d>=m){
             if(mp[a[r]])
             SAM::updata(mp[a[r]]);
             r--;
         }
         int ID=H::findp(H::root,Q[i].k);
         ans[Q[i].id]=SAM::pos[H::rec[ID]];
     }
     for(int i=;i<=q;i++) printf("%d\n",ans[i]);
 }