NFA 确定化为 DFA

子集法：

f(q,a)={q1,q2,…,qn},状态集的子集

将{q1,q2,…,qn}看做一个状态A，去记录NFA读入输入符号之后可能达到的所有状态的集合。

步骤：

1.根据NFA构造DFA状态转换矩阵

①确定DFA初态（NFA的所有初态集），字母表

②从初态出发，经字母表到达的状态集看成一个新状态

③将新状态添加到DFA状态集

④重复23步骤，直到没有新的DFA状态

2.画出DFA

3.看NFA和DFA识别的符号串是否一致。

练习：

1.解决多值映射：子集法

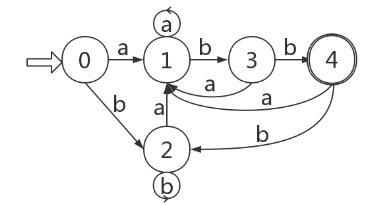
1）. 发给大家的图1

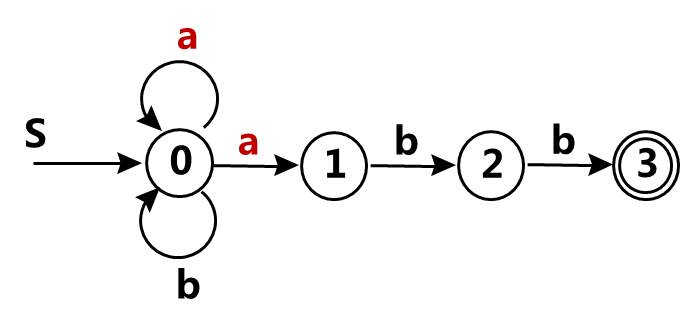
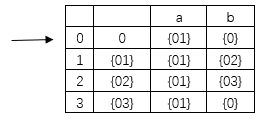
2）. P64页练习3

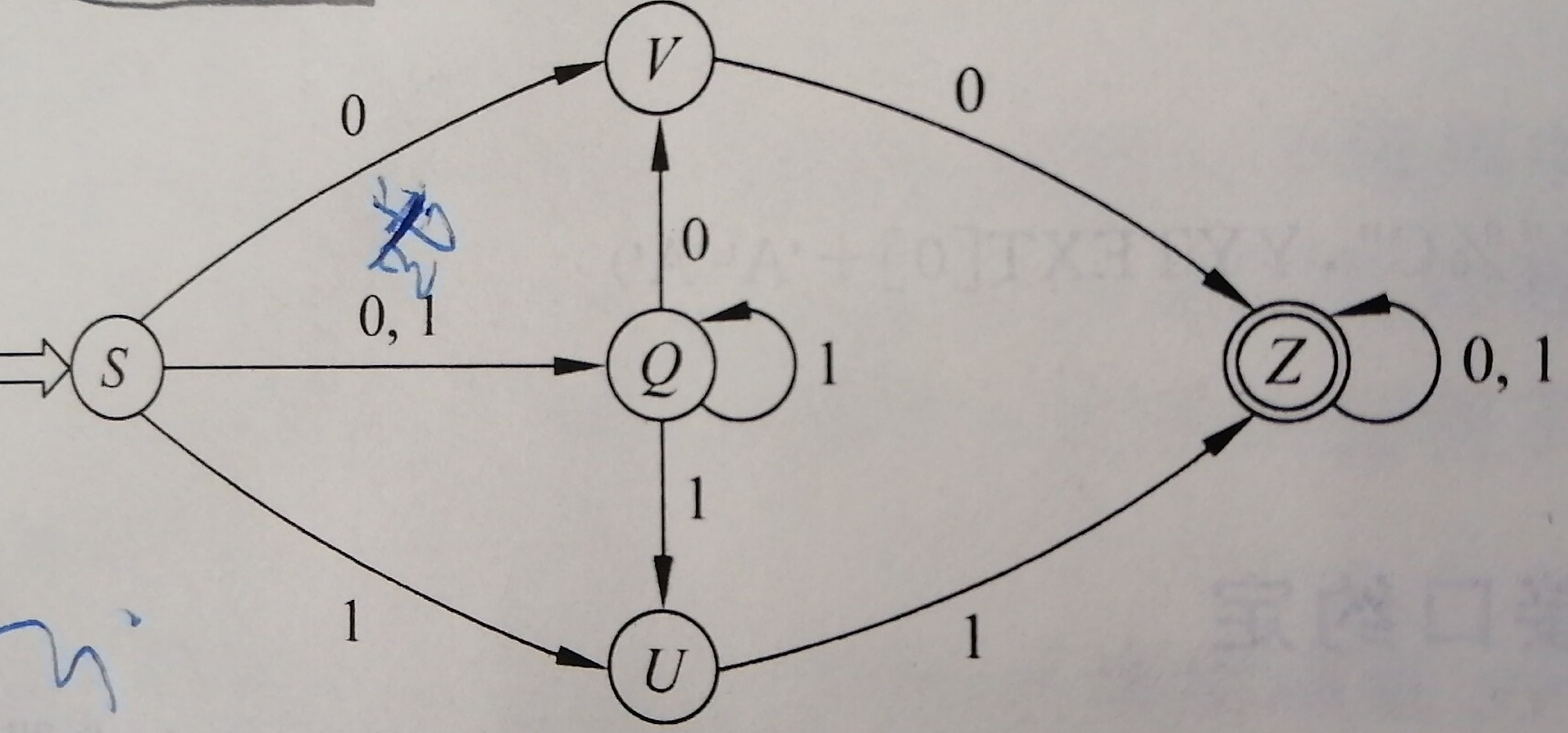
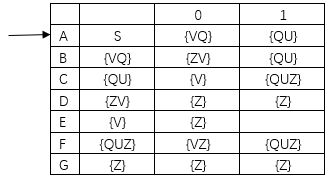
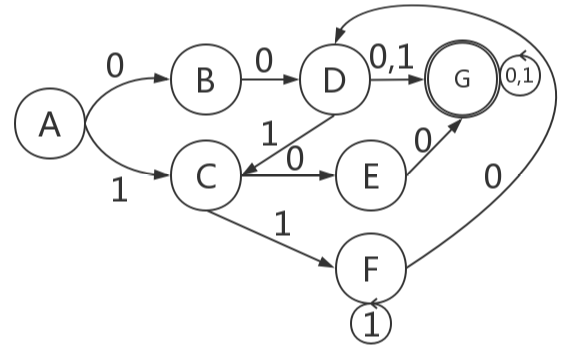
2.解决空弧：对初态和所有新状态求ε－闭包

1）. 发给大家的图2

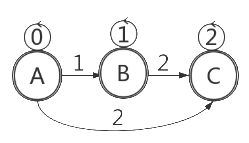
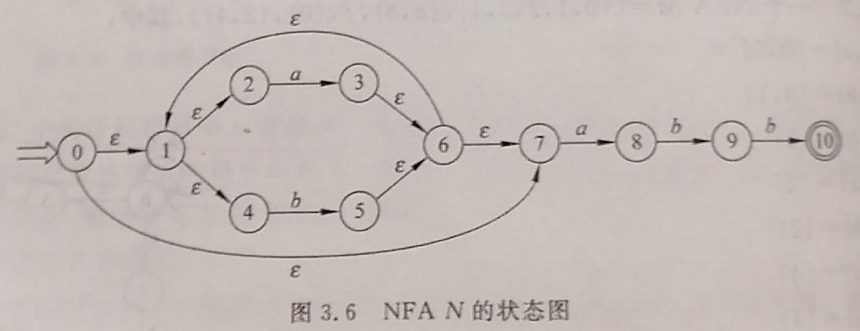
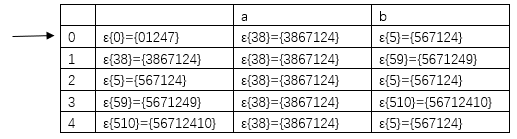
2）.P50图3.6

作业八——非确定的自动机NFA确定化为DFA的更多相关文章

  1. 第八次作业-非确定的自动机NFA确定化为DFA

    NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. 步骤: 1. ...

  2. 第八次-非确定的自动机NFA确定化为DFA

     提交作业 NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. ...

  3. 第八次——非确定的自动机NFA确定化为DFA

    NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. 步骤: 1. ...

  4. 非确定的自动机NFA确定化为DFA

    摘要: 在编译系统中,词法分析阶段是整个编译系统的基础.对于单词的识别,有限自动机FA是一种十分有效的工具.有限自动机由其映射f是否为单值而分为确定的有限自动机DFA和非确定的有限自动机NFA.在非确 ...

  5. 编译原理之非确定的自动机NFA确定化为DFA

    1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} ),其中 f(0,a)={0,1}  f(0,b)={0}  f(1,b)={2}  f(2,b)={3} 画出状态转换矩阵 ...

  6. 编译原理：非确定的自动机NFA确定化为DFA

    1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} ),其中 f(0,a)={0,1}  f(0,b)={0}  f(1,b)={2}  f(2,b)={3} 画出状态转换矩阵 ...

  7. NFA转化为DFA

    NFA(不确定的有穷自动机)转化为DFA(确定的有穷自动机) NFA转换DFA,通常是将带空串的NFA(即:ε-NFA)先转化为不带空串的NFA(即:NFA),然后再转化为DFA. 提示:ε是空串的意 ...

  8. 非确定有限状态自动机的构建（二）——将CharVal转换为NFA

    保留版权,转载注明出处:潘军彪的个人博客(http://blog.csdn.net/panjunbiao/article/details/9378933) 将上下文无关文法读入内存之后,可以将它转换成 ...

  9. 非确定有限状态自动机的构建（一）——NFA的定义和实现

    保留版权,转载需注明出处(http://blog.csdn.net/panjunbiao). 非确定有限状态自动机(Nondeterministic Finite Automata,NFA)由以下元素 ...

随机推荐

  1. vue学习中遇到的问题

    1.axios使用post传值时无法使用键值对传值的问题 问题的原因:主要是HTTP请求中的get请求和post请求参数的存放位置是不一样的,get请求的参数以键值对的方式跟在url后面的,而post ...

  2. sort(()=>{return Math.random()-0.5)}乱序数组不准确

    为什么sort(()=>{return Math.random()-0.5)}乱序数组不准确.(注意结合插入排序原理来理解) @1.chrome浏览器对于数组长度10以内为插入排序.反之则快速排 ...

  3. [Agc029D]Grid game_贪心

    Grid game 题目链接:https://atcoder.jp/contests/agc029/tasks/agc029_d 数据范围:略. 题解: 方法肯定很简单,就是找一处障碍待在他上面就好. ...

  4. 【AtCoder】diverta 2019 Programming Contest

    diverta 2019 Programming Contest 因为评测机的缘故--它unrated了.. A - Consecutive Integers #include <bits/st ...

  5. 如何使用RedisTemplate访问Redis数据结构之字符串操作

    Redis 数据结构简介 Redis 可以存储键与5种不同数据结构类型之间的映射,这5种数据结构类型分别为String(字符串).List(列表).Set(集合).Hash(散列)和 Zset(有序集 ...

  6. Java学习路径

    -------第一部分:基础语法-------- 1.输出语句 1.1 hello world 1.2 拼接输出.换行和不换行输出 1.3 拼接变量输出 2.输入语句: 2.1 定义变量,赋值(整数. ...

  7. DP+线段树维护矩阵（2019牛客暑期多校训练营（第二场））--MAZE

    题意:https://ac.nowcoder.com/acm/contest/882/E 给你01矩阵,有两种操作:1是把一个位置0变1.1变0,2是问你从第一行i开始,到最后一行j有几种走法.你只能 ...

  8. fiddler笔记：filters选项卡

    Host Show only Intranet Host 只显示内网(如不带"."的主机名)的数据流. Show only Internet Host 只显示互联网(如不带&quo ...

  9. 【思维】ABC

    题目描述 You are given a string s consisting of A, B and C.Snuke wants to perform the following operatio ...

  10. git bash配置SSH远程连接阿里云ECS

    1.连接配置 1-1.添加安全组规则 1-2.使用GitHub的话本地都会有id_rsa.pub(公钥),id_rsa(私钥),一般保存在C盘用户目录下.ssh文件夹. 把公钥内容复制下来(ssh-r ...