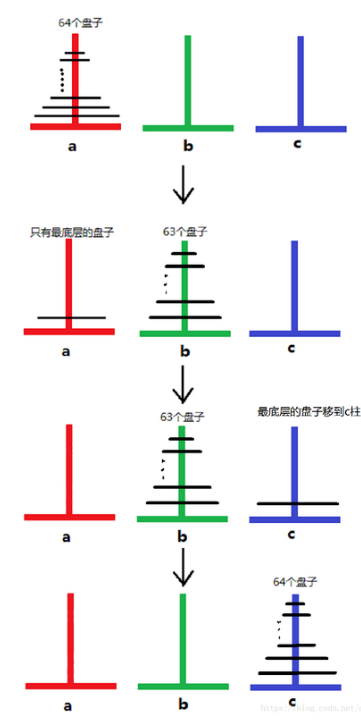
【Python实践-3】汉诺塔问题递归求解（打印移动步骤及计算移动步数）

 # -*- coding: utf-8 -*-
 #汉诺塔移动问题
 # 定义move(n,a,b,c)函数，接受参数n，表示3个柱子A、B、C中第1个柱子A的盘子数量
 # 然后打印出把所有盘子从A借助B移动到C的方法
 def move(n,a,b,c):
     if n==1:
         print('move', a, '-->', c)
     else:
         move(n-1,a,c,b)
         move(1,a,b,c)
         move(n-1,b,a,c)
 move(5,'A','B','C')

 #计算移动步数
 def f(n):
     if(n==1):
         return 1
     else:
         return 2*f(n-1)+1
 print(f(4))

 

知识点：

递归函数： 一个函数在内部调用自身本身。 递归函数的优点是定义简单，逻辑清晰。理论上，所有的递归函数都可以写成循环的方式，但循环的逻辑不如递归清晰。 使用递归函数需要注意防止栈溢出。 解决递归调用栈溢出的方法是通过尾递归优化， 尾递归是指，在函数返回的时候，调用自身本身，并且，return语句不能包含表达式。但是 大多数编程语言没有针对尾递归做优化，Python解释器也没有做优化， 任何递归函数都存在栈溢出的问题。

 

 

汉诺塔(Tower of Hanoi)源于印度传说中，大梵天创造世界时造了三根金钢石柱子，其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

a是起始柱，c是目标柱，b起到中转作用， 在进行转移操作时，都必须确保大盘在小盘下面，且每次只能移动一个圆盘，最终c柱上有所有的盘子且也是从上到下按从小到大的顺序。

问题看起来并不复杂，当a柱子上只有一个盘子时只要把那个盘子直接移到c， 有两个盘子的话把1号盘先移到b柱，在把2号盘移到c柱，最后把b柱上的1号盘移到c柱。

 

64个盘子，先把上方的63个盘子看成整体，等于只有两个盘，只要完成两个盘子的转移，然后假设a柱只有63个盘子，与之前一样的解决方式，前62个盘子先完成移动目标。就这样一步步向前找到可以直接移动的盘子，62,61,60，......，2,1，最终，最上方的盘子是可以直接移动到c柱的，此时2号盘也能完成向c柱的转移，这时c柱上时已经转移成功的2个盘，于是3号盘也可以了，一直到第64号盘。

 

理解小tip，我是这么理解的，先看只有两个盘子的移动方式：a-->b, a-->c, b-->c，之后盘子数增加，但都是基于两个盘子的这种转移方式，先将n-1个盘子移到中间柱b，此时等于中间柱b变成了目标柱，目标柱c变成了中间柱，所以此时是move(n-1,a,c,b)【可以看到b,c互换位置】，然后将1个盘子移到目标柱，即move(1,a,b,c)，最后将n-1个盘子从b移到c，此时等于是将b看成起始柱，将a看成中间柱，所以是move(n-1,b,a,c),这样就完成了移动。整个游戏中a为起始柱，b为中间柱，c为目标柱，在移动过程中，把一摞盘子从一个柱全部转移到另一个柱子，那么当前所在的就是起始柱，要移去的就是目标柱，另一个柱子就是中间柱，都是相对的，体现在代码中就是a,b,c参数位置的互换。结合网页汉诺塔小游戏理解更佳哦~