为什么样本方差的分母是n-1？为什么它又叫做无偏估计？

为什么样本方差的分母是n-1？最简单的原因，是因为因为均值已经用了n个数的平均来做估计在求方差时，只有(n-1)个数和均值信息是不相关的。而你的第ｎ个数已经可以由前(n-1)个数和均值　来唯一确定，实际上没有信息量。所以在计算方差时，只除以(n-1)。

那么更严格的证明呢？请耐心的看下去。

---

样本方差计算公式里分母为的目的是为了让方差的估计是无偏的。

无偏的估计(unbiased estimator)比有偏估计(biased estimator)更好是符合直觉的，尽管有的统计学家认为让mean square error即MSE最小才更有意义，这个问题我们不在这里探讨；不符合直觉的是，为什么分母必须得是而不是才能使得该估计无偏。

首先，我们假定随机变量的数学期望是已知的，然而方差未知。在这个条件下，根据方差的定义我们有

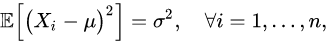
由此可得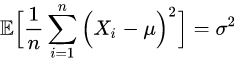

因此

是方差的一个无偏估计，注意式中的分母不偏不倚正好是！这个结果符合直觉，并且在数学上也是显而易见的。

现在，我们考虑随机变量的数学期望是未知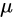的情形。这时，我们会倾向于无脑直接用样本均值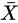替换掉上面式子中的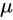。这样做有什么后果呢？后果就是，如果直接使用

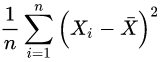
作为估计，那么你会倾向于低估方差！这是因为：

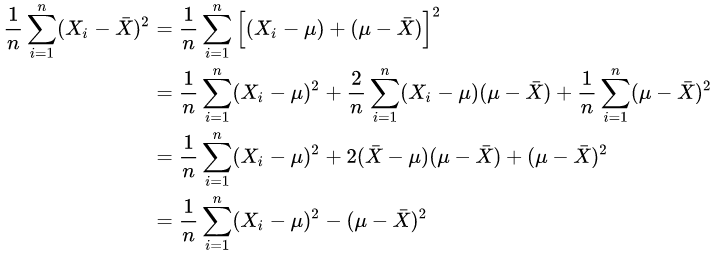
换言之，除非正好，否则我们一定有

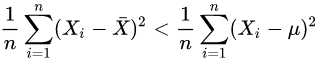
而不等式右边的那位才是的对方差的“正确”估计！这个不等式说明了，为什么直接使用

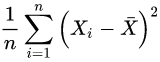
会导致对方差的低估。

那么，在不知道随机变量真实数学期望的前提下，如何“正确”的估计方差呢？答案是把上式中的分母n换成n-1，通过这种方法把原来的偏小的估计“放大”一点点，我们就能获得对方差的正确估计了：

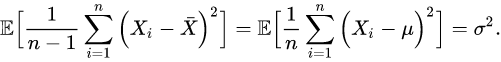
至于为什么分母是n-1而不是n-2或者别的什么数，最好还是去看真正的数学证明，因为数学证明的根本目的就是告诉人们“为什么”；暂时我没有办法给出更“初等”的解释了。

更多机器学习、编程、AI相关知识，也欢迎关注我的公众号“图灵的猫”。关注公众号，点击“学习资料”菜单，即可获得海量机器学习、深度学习书籍等免费PDF资源~