杭电oj_2047——阿牛的EOF牛肉串（java实现）

//20200322update

最近在重新把hdoj11页做一遍，发现递推还是有些模糊，就重新来更新下，新增一题2045

首先是2045题（RPG问题）

思路：分两种情况

1. 第n-1个元素和第一个元素同色，则第n-2个元素和第一个元素肯定不同色（因为之前的序列都是合法的），那么最后一个元素有两种选法，则这种情况的数量为2*f(n-2)

2. 第n-1个元素和第一个元素不同色，则最后一个格子只有一种选法，故这种情况数量为f(n-1)

故所有情况为二者之和

source code：

package hduoj;

import java.util.Scanner;

public class hdoj_2045 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        long[] res = new long[51];
        res[1] = 3;
        res[2] = 6;
        res[3] = 6;//注意第三个要单独列出，因为有三个元素的话，倒数第二个元素不可能和首元素相同
        for(int i = 4;i<51;++i){
            res[i] = res[i-1] + 2 * res[i-2];
        }

        while(sc.hasNext()){
            System.out.println(res[sc.nextInt()]);
        }
    }
}

接下来是2047题

这一题看了下我原来的博客，使用的找规律的方法，画出分支树然后找规律，这样比较难懂

所以换了一种做法，比上一种更好懂

思路：

也是分为两种情况

1. 最后一个元素是‘o’的字符串

2. 最后一个元素不是‘o’的字符串

创建一个n行2列的二维数组，将第一种情况的数量存在第一列，第二种存在第二列

则第n行的情况为

1. 最后一个元素为‘o’的字符串数量为n-1行第二列的数值（因为不能有两个‘o’连在一起）

2. 最后一个元素不是‘o’的字符串数量为两倍的n-1行所有数据的和（因为无论是哪种情况后面都可以加非‘o’字母，切有两种选法）

source code

import java.util.Scanner;
/**

*/
public class Main{

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        long[][] dp = new long[40][2];
        dp[0][0] = 1;
        dp[0][1] = 2;
        for(int i = 1;i<40;++i){
            dp[i][0] = dp[i-1][1];
            dp[i][1] = 2*(dp[i-1][1] + dp[i-1][0]);
        }

        while(sc.hasNext()){

            int i = sc.nextInt();
            System.out.println(dp[i-1][0] + dp[i-1][1]);
        }

    }

}

---------------------------------------------------------------------

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2047

思路：先是列出了四个，但是没发现规律，然后开始画递归树，在其中找到了规律，算出递归式为f(n) = 2*[f(n-1)+f(n-2)]

递归树分析如下（有点潦草，看不懂可以留言，大致模型为嵌套）：

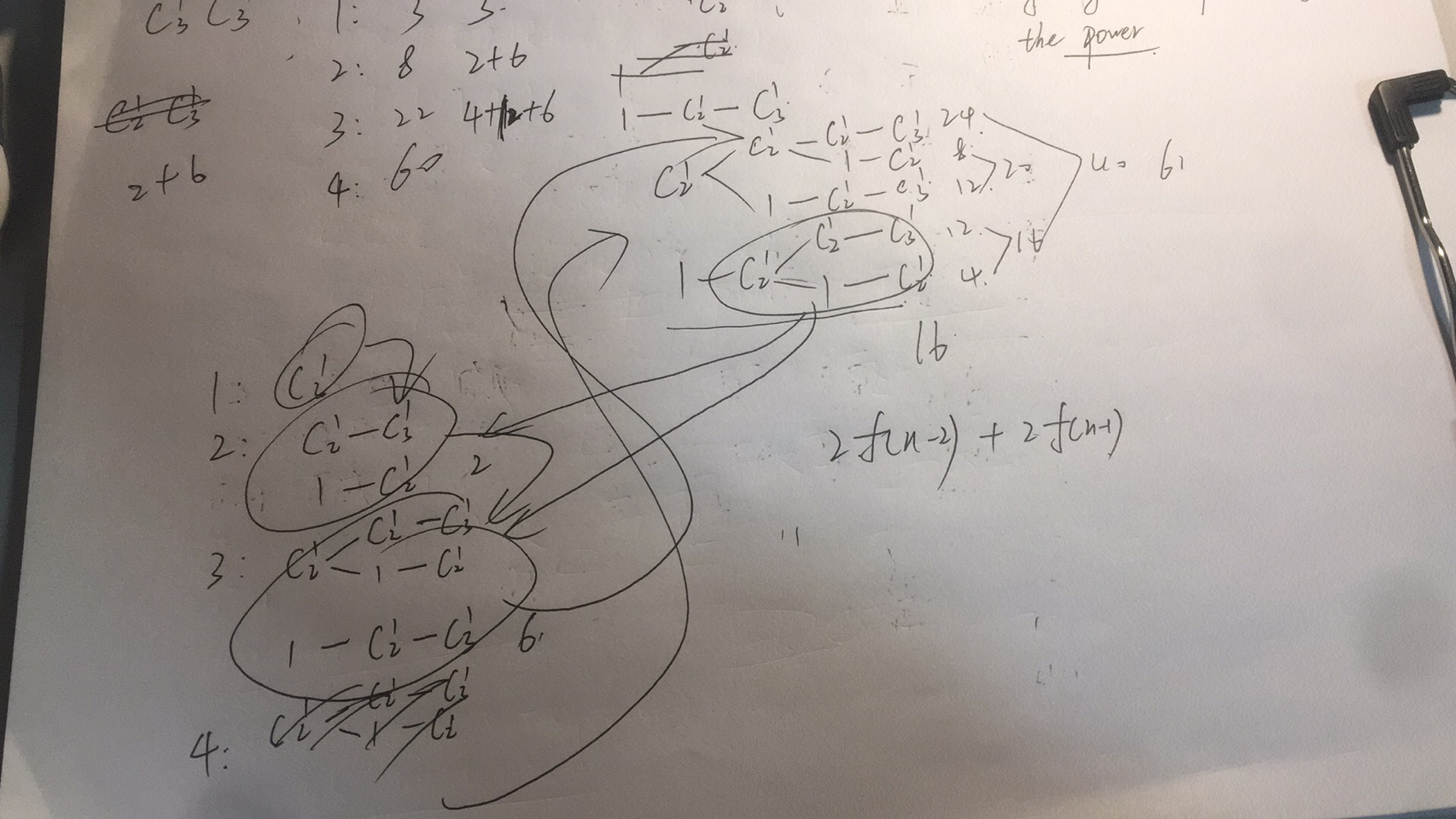
source code：

package hduoj;

import java.util.Scanner;

public class hdoj_2047 {
    /**
     * 得出递归式：f(n) = 2*[f(n-1)+f(n-2)]
     */
    public static void main(String[] args) {
        long[] data = new long[41];
        data[1] = 3;
        data[2] = 8;
        for(int  i = 3;i<41;++i){
            data[i] = 2*(data[i - 1]+data[i - 2]);
        }
        Scanner sc = new Scanner(System.in);
        while(sc.hasNext()){
            System.out.println(data[sc.nextInt()]);
        }
    }
}

代码已经ac

希望对大家有所帮助

以上