[BZOJ2876]骑行川藏
以前并没有发现微积分教材上有这种东西...我还是太菜了...
其实就是要在满足$\sum\limits_{i=1}^nk_is_i(v_i-v_i')^2\leq E$的同时求$\sum\limits_{i=1}^n\dfrac{s_i}{v_i}$的最小值
首先我们要跑得尽可能快,所以$v_i\geq v_i'$,而且在最优解体能是一定会被用完的,那么限制就变成等式了
拉格朗日乘数法可用于求多元函数的带限制极值:$g(x_1,\cdots,x_n)=0$,求$f(x_1,\cdots,x_n)$的极值
我看的书上有一个挺好的几何解释:把$f$的图像画出来,再在上面画一些“等高线”,同时把$g(x_1,\cdots,x_n)=0$和$f(x_1,\cdots,x_n)$的“交线”画出来,那么取到极值的地方就是等高线与交线相切的地方
比如说求$f(x,y)=x^2+y^2+2$在限制$g(x,y)=x^2+\dfrac14y^2-1=0$下的极值,三张图一目了然
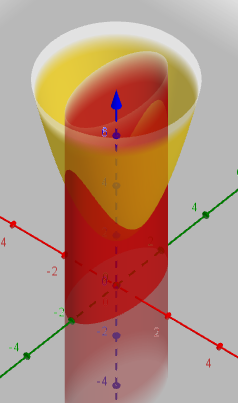 黄色:$z=f(x,y)$,红色:$g(x,y)=0$
黄色:$z=f(x,y)$,红色:$g(x,y)=0$
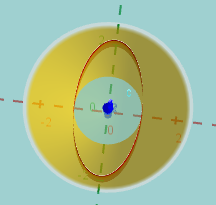 $z=2$
$z=2$
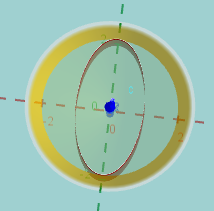 $z=6$
$z=6$
相切意味着梯度线性相关,即是说如果在$x_i=t_i$处$f$取得极值,那么$\nabla f(t_1,\cdots,t_n)=\lambda\nabla g(t_1,\cdots,t_n)$,我们把它拆分成关于每个变量的偏导,即对于$\forall1\leq i\leq n$有$\left.\dfrac{\partial f}{\partial x_i}\right|_{x_i=t_i}=\lambda\left.\dfrac{\partial g}{\partial x_i}\right|_{x_i=t_i}$
再加上$g(t_1,\cdots,t_n)=0$,总共$n+1$个变量和$n+1$条方程,可以解出来
再看这道题,限制条件是$\sum\limits_{i=1}^nk_is_i(v_i-v_i')^2-E=0$,我们要求$\sum\limits_{i=1}^n\dfrac{s_i}{v_i}$的极值,所以有方程$-\dfrac1{v_i^2}=2\lambda k_i(v_i-v_i')$,首先这说明$\lambda\lt0$,方程左边是经过三四象限的类双曲线,右边是斜率为负的经过第一象限的直线,所以当$\lambda$确定后有且只有一个$v_i$满足方程,并且因为$\lambda$越大,$v_i$也越大,这直接导致了$\sum\limits_{i=1}^nk_is_i(v_i-v_i')^2$变大,所以我们可以二分出满足关于$E$的限制的$\lambda$,在这个过程中求$v_i$也是可以二分的,于是我们就愉悦地做完了这题
注意精度...
#include<stdio.h>
typedef double du;
const du eps=1e-14,inf=1e9;
du s[10010],k[10010],v[10010];
int n;
du sqr(du x){return x*x;}
du calc(int i,du lm){
du l,r,mid;
l=eps;
r=inf;
while(r-l>eps){
mid=(l+r)*.5;
if(-1<2*lm*k[i]*(mid-v[i])*sqr(mid))
l=mid;
else
r=mid;
}
return mid;
}
du check(du lm){
int i;
du r=0;
for(i=1;i<=n;i++)r+=k[i]*s[i]*sqr(calc(i,lm)-v[i]);
return r;
}
int main(){
int i;
du E,l,r,mid,ans;
scanf("%d%lf",&n,&E);
for(i=1;i<=n;i++)scanf("%lf%lf%lf",s+i,k+i,v+i);
l=-inf;
r=-eps;
while(r-l>eps){
mid=(l+r)*.5;
if(check(mid)<E)
l=mid;
else
r=mid;
}
ans=0;
for(i=1;i<=n;i++)ans+=s[i]/calc(i,mid);
printf("%.10lf",ans);
}
[BZOJ2876]骑行川藏的更多相关文章
- 【BZOJ2876】【NOI2012】骑行川藏(数学,二分答案)
[BZOJ2876][NOI2012]骑行川藏(数学,二分答案) 题面 BZOJ 题解 我们有一个很有趣的思路. 首先我们给每条边随意的赋一个初值. 当然了,这个初值不会比这条边的风速小. 那么,我们 ...
- bzoj 2876: [Noi2012]骑行川藏 拉格朗日数乘
2876: [Noi2012]骑行川藏 Time Limit: 20 Sec Memory Limit: 128 MBSec Special JudgeSubmit: 1033 Solved: ...
- 高等数学(拉格朗日乘子法):NOI 2012 骑行川藏
[NOI2012] 骑行川藏 输入文件:bicycling.in 输出文件:bicycling.out 评测插件 时间限制:1 s 内存限制:128 MB NOI2012 Day1 Des ...
- BZOJ 2876 【NOI2012】 骑行川藏
题目链接:骑行川藏 听说这道题需要一些高数知识 于是膜了一发dalao的题解……然后就没了…… 不要吐槽我的精度TAT……eps设太小了就TLE,大了就Wa……我二分的边界是对着数据卡的…… 下面贴代 ...
- 「NOI2012」骑行川藏
「NOI2012」骑行川藏 题目描述 蛋蛋非常热衷于挑战自我,今年暑假他准备沿川藏线骑着自行车从成都前往拉萨. 川藏线的沿途有着非常美丽的风景,但在这一路上也有着很多的艰难险阻,路况变化多端,而蛋蛋的 ...
- bzoj2876 [Noi2012]骑行川藏
Description 蛋蛋非常热衷于挑战自我,今年暑假他准备沿川藏线骑着自行车从成都前往拉萨.川藏线的沿途有着非常美丽的风景,但在这一路上也有着很多的艰难险阻,路况变化多端,而蛋蛋的体力十分有限,因 ...
- bzoj2876 [NOI2012]骑行川藏(拉格朗日乘数法)
题目描述 蛋蛋非常热衷于挑战自我,今年暑假他准备沿川藏线骑着自行车从成都前往拉萨.川藏线的沿途有着非常美丽的风景,但在这一路上也有着很多的艰难险阻,路况变化多端,而蛋蛋的体力十分有限,因此在每天的骑行 ...
- 2876: [Noi2012]骑行川藏 - BZOJ
Description 蛋蛋非常热衷于挑战自我,今年暑假他准备沿川藏线骑着自行车从成都前往拉萨.川藏线的沿途有着非常美丽的风景,但在这一路上也有着很多的艰难险阻,路况变化多端,而蛋蛋的体力十分有限,因 ...
- 【NOI2012】骑行川藏
获得成就:第一次在信竞做神仙数学题 先放个前言,$OI$ 出大型数学题还是比较麻烦的,因为主要是考你数学推导 / 手算式子,你算出来之后把公式套个板子,就得到结论——$OI$ 的大型数学题的代码都是板 ...
随机推荐
- NEYC 2017 自动取款机 atm Day6 T1
自动取款机 [问题描述] 小 ...
- codeforces902B. Coloring a Tree
B. Coloring a Tree 题目链接: https://codeforces.com/contest/902/problem/B 题意:给你一颗树,原先是没有颜色的,需要你给树填色成指定的样 ...
- webpack 小记
零.入口与输出 //对像语法 entry: { aa: __dirname + '/src/aa.js', //(chunkName :path) bb: __dirname + '/src/b ...
- 单选按钮radio与文字如何对齐?
布局如下: <input type="radio" value="立即发送" name="a_1">立即发送 <input ...
- MySql数据库学习总结(MySQL入门到精通)
2017.1.24-2.3日(在大兴实验室) 1.数据库存储引擎: (1)MyISAM: 访问速度快,对事物完整性没要求,并以访问为主的适合这个 (2)InnoDB: 更占磁盘空间,需要进行频繁的更新 ...
- Idea IntelliJ远程调试教程
总结 第一步:修改startup.sh 在倒第二行加上export JPDA_ADDRESS=8787 最后一行在start前面加上" jpda " 第二步:配置Idea, ...
- 【Foreign】字符串匹配 [KMP]
字符串匹配 Time Limit: 10 Sec Memory Limit: 256 MB Description Input Output Sample Input 3 3 6 3 1 2 1 2 ...
- bzoj 2753 最小生成树变形
我们根据高度建图,将无向边转化为有向边 首先对于第一问,直接一个bfs搞定,得到ans1 然后第二问,我们就相当于要求找到一颗最小生成树, 满足相对来说深度小的高度大,也就是要以高度为优先级 假设现在 ...
- MFC/Socket网络编程
转载: https://jingyan.baidu.com/article/676629974557c254d51b84da.html
- linux系统备份脚本
前言 之前写过<<linux系统简单备份的脚本>>, 最开始一直用着,后来觉得有必要改进下它,不管是从操作方式上还是脚本的工作方式上.之所以这么看重备份,是因为我经历过磁盘损坏 ...
