从BST到LSM的进阶之路

前言

相信大家之前都了解过很多种数据结构，我之前总是两两的，也就是从局部上去进行比较，没有从整体上进行这些树的发展脉络进行梳理，因此经常看完没多久就忘了。看来确实是需要从本源出发，不仅要知其然还要知其所以然，了解清楚前因后果，不仅可以方便我们记忆，更有利于增加我们的理解深度。实际上任何事物的出现都是有他出现的必要性，当某个事物达到瓶颈之后，必然会出现新的事务来弥补它的不足。好的，废话不多说了，今天我们就从一个小的BST开始，一起见证一下它的升级打怪之路吧。

开场之前，先来两颗开胃小树

完全二叉树：

金无足赤，人无完人，但是二叉树是可以有完美的，所有叶子都位于相同的水平的二叉树就是完全二叉树。

平衡二叉树：

树也是有等级之分的，不是所有的树都是完美的，相比完美二叉树，稍微低一等级的叫平衡二叉树。每个节点的平衡因子在-1到1之间的，虽然不是完全平衡的，但是也还能接受。

二叉搜索树(BST)：

二叉搜索树（balance search tree），这是一棵有组织有纪律的树，满足左子树中所有节点的值小于根的值，右子树中所有节点的值大于或等于根的值。简单说就是有序的，所以在查询的时候就可以使用二分法，因此具有很高的查询效率，最佳的时间复杂度是o(log n)，最差是O(n)。当一颗二叉搜索树是一组升序或者降序的数值时，二叉搜索树就会退化为单链表，查找时间复杂度变成了O(n)。

AVL树

为什么会有AVL树

前边提到了，当向BST中插入一组有序的数值时，就会退化为单链表，性能会退化到o(n)，究其根源是因为小时候父母管的比较松，任由她自由发展，导致BST偏科了，能力没有得到均衡发展，所以怎么办呢？嗯，没错，是得请个家教，而且一个不够，得两个，制定个规则去约束她，即使不能像完美二叉树那样科科满分，至少也得平衡一些是吧，要不都嫁不出去啦。请了家教之后，BST直接鸟枪换炮，摇身一变成为了我们接下来要介绍的AVL树。

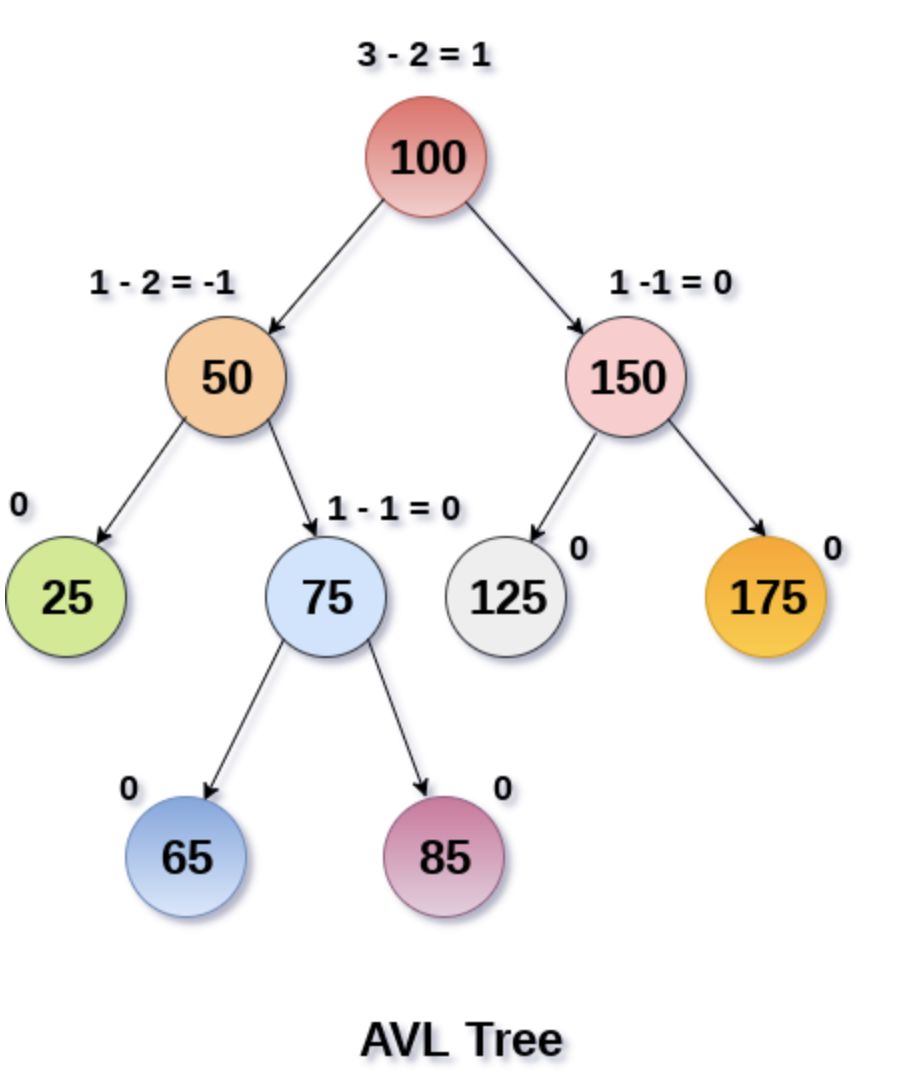
什么是AVL树

AVL树指的是平衡二叉搜索树，没错它就是二叉搜索树和平衡二叉树杂交育种的结果，结合了双亲的优良特性，有序且平衡，直接走向树生巅峰。

为什么叫AVL树？这可不是取的平衡二叉搜索树首字母的缩写，而是因为是BST的两个家教的name是G. M. Adelson-Velsky和Evgenii Landis。

AVL树的查找，插入和删除的时间复杂度都固定是o(log n)，但是增加和删除操作会使树失去平衡，因此需要通过一次或多次树旋转来重新平衡这棵树。

旋转分为LL，LR，RR，RL4种方式，具体的插入和删除的情况比较多，在这就不详细展开了，说一下关键的一点，是可能需要多次旋转来维持平衡，因此维护树保持平衡的成本还是蛮高的嘞，这也正是AVL树的弊端。

红黑树

为什么会出现红黑树

AVL树的左右子树高度差不能超过1，每次进行插入/删除操作时，几乎都需要通过旋转操作保持平衡，在频繁进行插入/删除的场景中，频繁的旋转操作使得AVL的性能大打折扣，所以就有了红黑树的出现。

什么是红黑树

红黑树是一种自平衡的二叉搜索树，和AVL树十分类似，红黑树的查找，插入和删除的时间复杂度都是o(log n)。但是红黑树不是一颗严格的平衡二叉树，它不像AVL树那样严格维持平衡因子为1来保持平衡，而是通过左旋，右旋和变色3种操作，维持自身的5大特性，保证了最长路径不超过最短路径的两倍，从而实现近似的平衡。

红黑树和AVL树的对比：

查找，插入和删除的时间复杂度都是o(log n)，相比于AVL树，红黑树牺牲了部分的平衡性，来换取了在插入和删除时更少的旋转的操作，因为整体性能上要优于AVL树，所以在查询场景多，插入和删除稍作少的场景，AVL树的性能更好，当插入和删除场景很多的时候，红黑树的性能更佳。

B树

为什么会出现B树

传统用来搜索的平衡二叉树有很多，如 AVL 树，红黑树等。这些树在一般情况下查询性能非常好，但当数据非常大的时候它们就无能为力了。原因当数据量非常大时，内存不够用，大部分数据只能存放在磁盘上，只有需要的数据才加载到内存中。一般而言内存访问的时间约为 50 ns，而磁盘在 10 ms 左右。速度相差了近 5 个数量级，磁盘读取时间远远超过了数据在内存中比较的时间。这说明程序大部分时间会阻塞在磁盘 IO 上。那么我们如何提高程序性能？减少磁盘 IO 次数，像 AVL 树，红黑树这类平衡二叉树从设计上无法“迎合”磁盘。

平衡二叉树是通过旋转来保持平衡的，而旋转是对整棵树的操作，若部分加载到内存中则无法完成旋转操作。其次平衡二叉树的高度相对较大为 log n（底数为2），这样逻辑上很近的节点实际可能非常远，无法很好的利用磁盘预读（局部性原理），所以这类平衡二叉树在数据库和文件系统上的选择就被 pass 了。

什么是B树

B树是一种多路平衡查找树，相对于二叉树而言，B树可以认为是一颗多叉树，m阶B树表示一个节点最多有m个子节点。

下面我们来看看B树的定义。

• 每个节点最多有m-1个关键字（可以存有的键值对）。
• 根节点最少可以只有1个关键字。
• 非根节点至少有m/2个关键字。
• 每个节点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
• 所有叶子节点都位于同一层，或者说根节点到每个叶子节点的长度都相同。
• 每个节点都存有索引和数据，也就是对应的key和value。

所以，根节点的关键字数量范围：1 <= k <= m-1，非根节点的关键字数量范围：m/2 <= k <= m-1。

B树和AVL树、红黑树一样，也是一颗自平衡的查找树，当新插入的节点不满足要求时，也会进行维权运动，只不过B树不会去旋转了，而是分裂，核心临界条件是每个节点关键字的数量，如果数量超出要求，那她就会进行分裂。

简单说一下分裂的过程，假如一颗4阶B树，当新插入元素后，某个节点的关键字数量达到4个，因为每个节点最多有m-1个关键字，也就是最多只能有3个节点，这时候就需要进行分裂。假设key的值为5，6，7，8，那会以m/2为界分为3个部分，5---6---7，8，分裂会将6放入父节点，5和7，8两个节点分别指向父节点。

这也就是说B树的分裂只会影响父节点和当前节点。

B+树

什么是B+树

特性：

1. B+树包含2种类型的节点：内部节点（也称索引节点）和叶子节点。根节点本身即可以是内部节点，也可以是叶子节点。根节点的关键字key个数最少可以只有1个；
2. B+树与B树最大的不同是内部节点不保存数据，只用于索引，所有数据（或者说记录）都保存在叶子节点中；
3. m阶B+树表示了内部节点最多有m-1个关键字（或者说内部节点最多有m个子树，和B树相同），阶数m同时限制了叶子节点最多存储m-1个记录；
4. 内部节点中的key都按照从小到大的顺序排列，对于内部节点中的一个key，左树中的所有key都小于它，右子树中的key都大于等于它。叶子节点中的记录也按照key的大小排列；
5. 每个叶子节点都存有相邻叶子节点的指针，叶子节点本身依关键字的大小自小而大顺序链接；

B+树和B树的对比：

B+树和B树的核心区别是，B树的每个节点都存储索引和数据，而B+树只有叶子节点存储了索引和数据，非叶子节点只存储索引，B+树相对于B树的优点，有如下3点：

• 磁盘IO次数少

因为B+树只有叶子节点存储了数据，其他非叶子节点只保存和索引，所以B+树单次磁盘IO的数量是要大于B树的，这就意味着B+树可以减少磁盘IO的次数，而我们都知道访问磁盘的速度比直接访问内存，要慢了不知道多少倍，所以磁盘IO的次数往往会成为性能的瓶颈点，因此磁盘IO次数少，可以大幅的提升插入和查询效率。

• 适合范围查询

B+树叶子节点形成有序链表，范围查询转化为顺序读，效率高。相对而言B树必须通过中序遍历才能支持范围查询。

• 查询性能稳定

因为B+树的数据全都保存在叶子节点上，因此每次必须要遍历到叶子节点，因此查询时间复杂度固定为O(log n)，而B树的数据直接保存在每个节点上，因此B树的查询时间复杂度在O(1)和O(log n)之间。

B+树的缺点

B+树的主要缺点有两个：

• 如果写入的数据比较离散，那么寻找写入位置时，子节点有很大可能性不会在内存中，最终会产生大量的随机写，性能下降。
• 如果B+树已经运行了很长时间，写入了很多数据，随着叶子节点分裂，其对应的块会不再顺序存储，而变得分散。这时执行范围查询也会变成随机读，效率降低了。

LSM树

为什么会出现LSM树

B+树作为mysql的索引结构，长期以来主流使用B+树这种索引结构来实现快速数据查找，具有很好的读性能。当数据量不太大时，B+树读写性能表现也非常好。但是在海量数据情况下，经常性的会有大量的数据的写入和更新，B+树越来越高，由于B+树更新和删除数据时需要沿着B+树逐层进行页分裂和页合并，当有大量分裂时，会导致大量的磁盘随机寻道，严重影响数据写入性能。LSM-tree就是为了解决上述问题而生的一种存储结构。

什么是LSM树

LSM Tree出现于谷歌的三驾马车之一的《Bigtable: A Distributed Storage System for Structured Data》，全称为Log-Structured Merge Tree，是一个分层、有序、针对块存储设备（机械硬盘和SSD）特点而设计的数据存储结构。

很多流行的数据库都有它的身影，比如Cassandra、RocksDB、HBase、LevelDB等NoSQL数据库，TiDB等newSQL数据库，甚至像SQLite这种传统的关系型数据库和MongoDB这种传统的文档型数据库，以及clickhouse都提供了基于LSM Tree的存储引擎作为可选的存储引擎。

它的核心理论基础还是磁盘的顺序写速度比随机写速度快非常多，即使是SSD，由于块擦除和垃圾回收的影响，顺序写速度还是比随机写速度快很多。

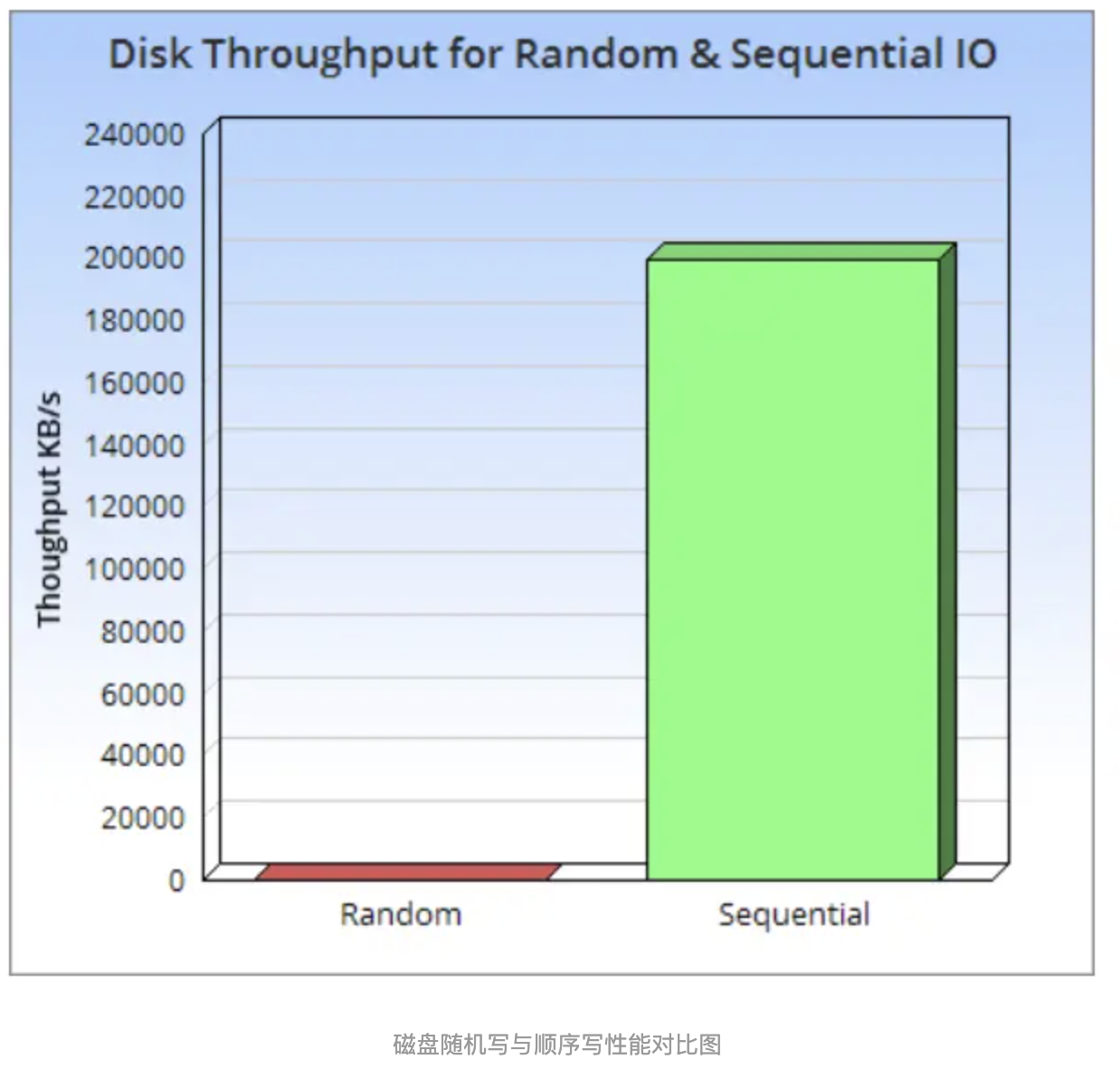
基本组成

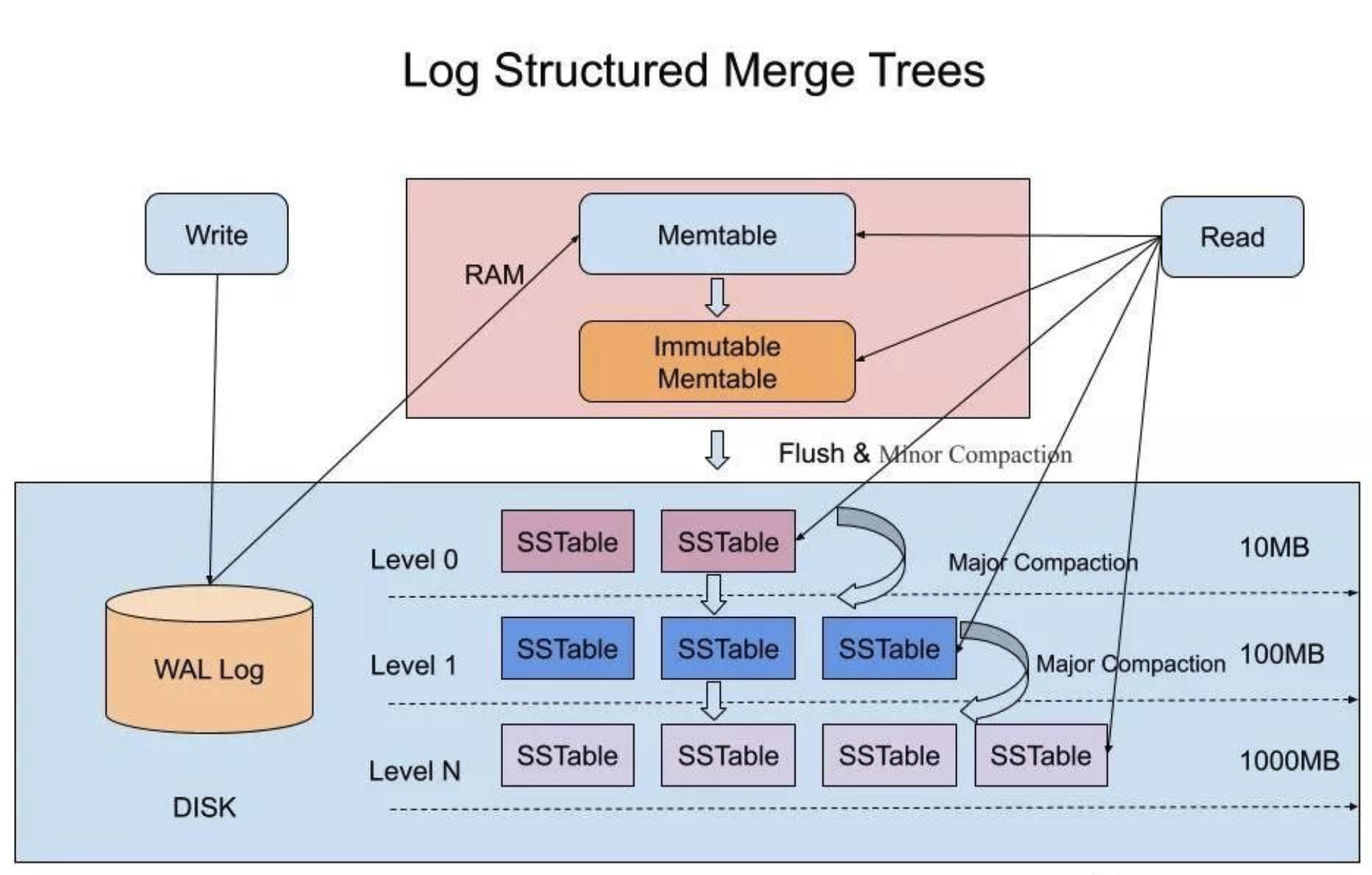
• WAL（write ahead log）

WAL的结构和作用跟其他数据库一样，是一个只能在尾部以Append Only方式追加记录的日志结构文件，它用来当系统崩溃重启时重放操作，使MemTable和Immutable MemTable中未持久化到磁盘中的数据不会丢失。

• MemTable

MemTable是内存中的数据结构，用于写入和读取最近更新的数据，MemTable具体的数据结构，LSM并没有强约束，可以是红黑树，也可以是跳表结构。需要支持高效的动态插入数据，对数据进行排序，也支持高效的对数据进行精确查找和范围查找。

• Immutable MemTable

当MemTable达到阈值的大小后，会转化为Immutable MemTable。Immutable MemTable不能写数据，只能读数据，定期会将Immutable MemTable的数据flush到磁盘中。

• SSTable(Sorted String Table)

SSTable是一种拥有持久化，有序且不可变的的键值存储结构，它的key和value都是任意的字节数组，并且了提供了按指定key查找和指定范围的key区间迭代遍历的功能。SSTable内部包含了一系列可配置大小的Block块，典型的大小是64KB，关于这些Block块的index存储在SSTable的尾部，用于帮助快速查找特定的Block。当一个SSTable被打开的时候，index会被加载到内存，然后根据key在内存index里面进行一个二分查找，查到该key对应的磁盘的offset之后，然后去磁盘把响应的块数据读取出来。当然如果内存足够大的话，可以直接把SSTable直接通过MMap的技术映射到内存中，从而提供更快的查找。

写流程

LSM-tree写入数据时，会先写一条记录到WAL中，然后会将数据写入内存中的MemTable中，当然内存的大小肯定是有限制的，不可能一直往里写，当MemTable的大小达到设定的阈值后，MemTable会转换为Immutable MemTable，顾名思义就是不可变的MemTable，然后会生成一个新的MemTable，用来写入新的数据。所以说MemTable只会有一个，但是Immutable MemTable可能会有多个。会有单独的线程定期的将Immutable MemTable的数据flush到磁盘中的SSTable中。

删数数据的时候与写入新数据一样，都是写入一条新的记录，只是删除数据时会添加一个删除标记，只有再compact时才会对带有删除标记的数据进行物理删除。

读流程

先在内存MemTable中查找，然后在内存中的Immutable MemTable中查找，然后在level 0 SSTable中查找，最后在level N SSTable中查找。

查找某个具体的SSTable时，一般先把SSTable的元数据block读到内存中，根据BloomFilter可以快速确定数据在当前SSTable中是否存在，如果存在，则采用二分法确定数据在哪个数据block，然后将相应数据block读到内存中进行精确查找。

从LSM Tree数据查找过程我们可以看到，为了查找到目标数据，我们需要读取并查找不包含目标数据的SSTable，如果目标数据在最底层level N的SSTable中，我们需要读取和查找所有的SSTable！LSM Tree把这种读取和查找了无关SSTable的现象叫做读放大(read amplification)。

读放大现象严重影响了LSM Tree数据查找性能，论文《BigTable》提到了几种提升数据查找性能的方法，如压缩，缓存，索引(布隆过滤器)以及compact等操作，这里就不详细展开了。

LSM树和B+树的对比

LSM树和B+树的差异主要在于读性能和写性能进行权衡

当写多读少的场景，LSM树相比于B树有更好的性能。因为大量的插入操作，为了维护B+树结构，节点分裂。读磁盘的随机读写概率会变大，性能会逐渐减弱。

当读多写少的场景，B+树相比于LSM树有更好的性能。LSM树通过牺牲部分读性能为代价，来大幅提升写性能，并且通过一些优化手段，如布隆过滤器和compact策略，对读性能有了很大的优化，时间复杂度也是O(log n)级别的。

参考文档：

https://www.cnblogs.com/wxiaotong/p/14781753.html

https://www.jianshu.com/p/f911cb9e42de

作者：京东物流 于建飞

来源：京东云开发者社区 自圆其说Tech 转载请注明来源