PCA主成分分析的理解

• u     |_matrix1x2_{{-0.70710678118654757};{-0.70710678118654735}}
• x^(1)    |_matrix1x2_{{-0.51805350077523271};{-1.5767841510657621}}
• x_approx^(1)   |_matrix1x2_{{-1.0474188259204973};{-1.0474188259204971}}
  • X_rec = Z * U(:,1:K)';
• z^(1)  |_matrix1x2_{{1.4812739091016711};{0}}
  • Ureduce = U(:, 1:K);  

    Z = X * Ureduce;
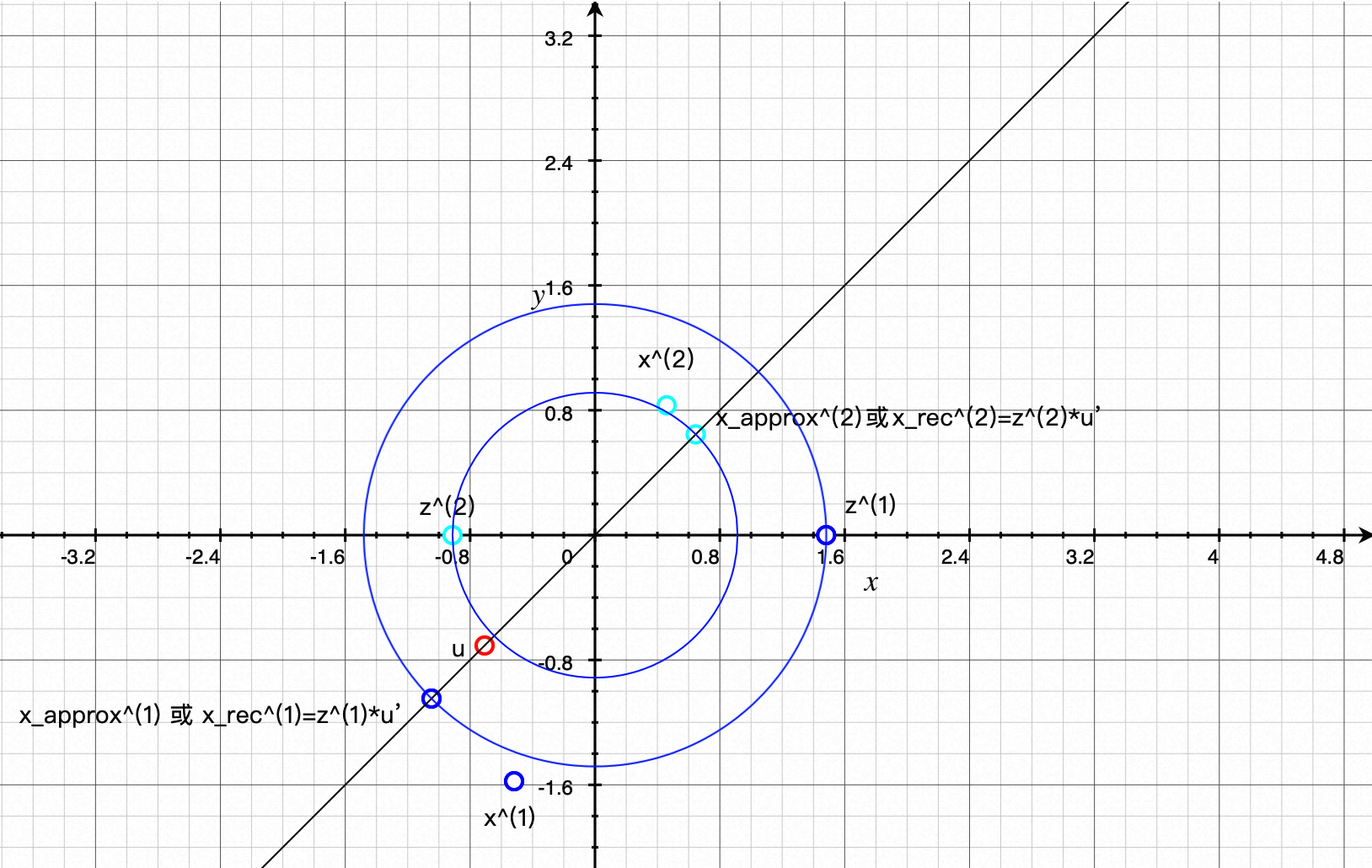
• 经过z^(1)的圆：x^{2}+y^{2}=2.194172393785345，发现正好也经过x_approx^(1)，说明x^(1)在方向向量u上的投影点x_approx^(1)（二维）距离原点的长度  ==  z^(1)的长度（一维）
  • PCA：特征向量x^(1)从二维 降低 为特征向量z^(1)一维
• x^(2)  |_matrix1x2_{{0.45915360635654012};{0.83189933545433081}}
• x_approx^(2)   |_matrix1x2_{{0.64552647090543547};{0.64552647090543525}}
• z^(2)    |_matrix1x2_{{-0.91291229002530794};{0}}
• 经过z^(2)的圆：x^{2}+y^{2}=0.833408849279252   （Grapher曲线着色不熟悉，应该为z^2)同色更好分辨）