ROC，AUC，PR，AP介绍及python绘制

这里介绍一下如题所述的四个概念以及相应的使用python绘制曲线：

参考博客：http://kubicode.me/2016/09/19/Machine%20Learning/AUC-Calculation-by-Python/?utm_source=tuicool&utm_medium=referral

一般我们在评判一个分类模型的好坏时，一般使用MAP值来衡量，MAP越接近1，模型效果越好；

更详细的可参考：http://www.cnblogs.com/pinard/p/5993450.html

准确率pr就是找得对，召回率rc就是找得全。
大概就是你问问一个模型，这堆东西是不是某个类的时候，准确率就是 它说是，这东西就确实是的概率吧，召回率就是， 它说是，但它漏说了（1-召回率）这么多。

（这里的P=FN+TP；N=TN+FP；而这里recall=tp rate;上述链接里的特异性其实就是fp rate）

AUC和AP分别是ROC和PR曲线下面积，map就是每个类的ap的平均值；python代码（IDE是jupyter notebook）：

#绘制二分类ROC曲线
import pylab as pl
%matplotlib inline
from math import log,exp,sqrt

evaluate_result = "D:/python_sth/1.txt"
db = []
pos , neg = 0 , 0
with open(evaluate_result , 'r') as fs:
    for line in fs:
        nonclk , clk , score = line.strip().split('\t')
        nonclk = int(nonclk)
        clk = int(clk)
        score = float(score)
        db.append([score , nonclk , clk])
        pos += clk
        neg += nonclk

db = sorted(db , key = lambda x:x[0] , reverse = True) #降序

#计算ROC坐标点
xy_arr = []
tp , fp = 0. , 0.
for i in range(len(db)):
    tp += db[i][2]
    fp += db[i][1]
    xy_arr.append([tp/neg , fp/pos])

#计算曲线下面积即AUC
auc = 0.
prev_x = 0
for x ,y in xy_arr:
    if x != prev_x:
        auc += (x - prev_x) * y
        prev_x = x
print "the auc is %s."%auc
x = [_v[0] for _v in xy_arr]
y = [_v[1] for _v in xy_arr]
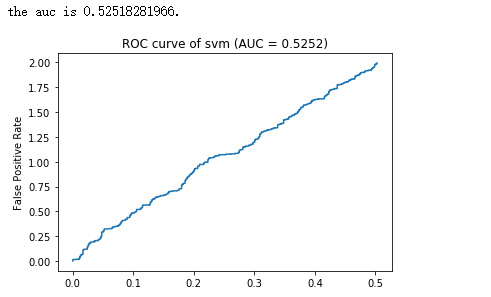
pl.title("ROC curve of %s (AUC = %.4f)" % ('svm' , auc))
pl.ylabel("False Positive Rate")
pl.plot(x ,y)
pl.show()

结果：（注意：ROC曲线中纵坐标是TP，横坐标是FP，下面的图有误！）

这里的.txt文件格式如：http://kubicode.me/img/AUC-Calculation-by-Python/evaluate_result.txt

形式为：

PS:该txt文件表示的意思是，比如对于第一行就是说：有一个样本得分为0.86...，并被预测为负样本；倒数第一行就是说，这么多测试样本中，有一个样本得分为0.45...，并被预测为正样本；

注意：绘制ROC和PR曲线时都是设定不同的阈值来获得对应的坐标，从而画出曲线

代码中：

1. nonclick:未点击的数据，可以看做负样本的数量
2. clk:点击的数量，可以看做正样本的数量
3. score:预测的分数，以该分数为group进行正负样本的预统计可以减少AUC的计算量
4. 代码中首先使用 

   db = sorted(db , key = lambda x:x[0] , reverse = True) 进行降序排序，然后将每一个从小到大的得分值作为阈值，每次得到一个fpr和tpr（因为最后得分大于阈值，就认为它是正样本，所以若.txt中得分为某一个阈值时nonclk为非0的数，而clk是0，则认为nonclk的值大小的样本是fp样本），最后画出曲线；

对于PR曲线也一样，只不过横坐标换成，纵坐标换成,AP是其曲线下面积；

上面的python代码针对二分类模型，但针对多分类模型时一样，即对于每个类都将其看做正样本，其他类看成负样本来画曲线，这样有多少类就画多少条相应的曲线，MAp值即为各类ap值的平均值；

PR曲线的绘制：

这里我们用一张图片作为例子，多张图片道理一样。假设一张图片有N个需要检测的目标，分别是object1,object2,object3共分为三类，使用检测器得到了M个Bounding Box(BB)，每个BB里包含BB所在的位置以及object1,object2,object3对应的分数confidence。
我把计算目标检测评价指标归为一下几步：
1，对每一类i进行如下操作：
对M个BB中每一个BB，计算其与N个GroundTruth（GT）的IoU值，且取其中的最大值MaxIoU。设定一个阈值thresh，一般设置thresh为0.5。当MaxIoU < thresh的时候，记录其类别i的分数confidencei以及fpi = 1，当MaxIoU>=thresh分为以下俩种情况：
当MaxIoU对应的GT类别为i的时候，记录其类别i的分数以及tpi = 1。
当MaxIoU对应的GT类别不为i的时候，记录其类别i的分数以及fpi = 1。
2，由步骤1我们可以得到3M个分数与tp/fp的元祖，形如(confidencei,tp或者fp)，对这3M个元祖按照confidence进行排序（从大到小）。
3，按照顺序1，2，3，4。。。M截取，计算每次截取所获得的recall和precision
recall = tp/N
precision = tp/tp+fp
这样得到M个recall和precision点，便画出PR曲线了~
计算AP值：

由上面得到了PR曲线，即得到了n个(P,R)坐标点，利用这些坐标点我们便可以计算出AP（average precision）:

方法一：11点法，此处参考的是PASCAL  VOC  CHALLENGE的计算方法。首先设定一组阈值，[0, 0.1, 0.2, …, 1]。然后对于recall大于每一个阈值（比如recall>0.3），我们都会得到一个对应的最大precision。这样，我们就计算出了11个precision。AP即为这11个precision的平均值。这种方法英文叫做11-point interpolated average precision。；

方法二：当然PASCAL VOC CHALLENGE自2010年后就换了另一种计算方法。新的计算方法假设这N个样本中有M个正例，那么我们会得到M个recall值（1/M, 2/M, …, M/M）,对于每个recall值r，我们可以计算出对应（r’ > r）的最大precision，然后对这M个precision值取平均即得到最后的AP值。

下面给出个例子方便更加形象的理解：

假设从测试集中共检测出20个例子，而测试集中共有6个正例，则PR表如下：

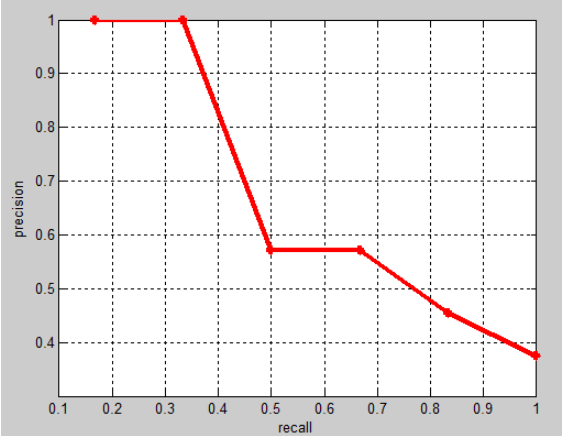
相应的Precision-Recall曲线（这条曲线是单调递减的）如下：

faster rcnn中计算map的代码：https://github.com/rbgirshick/py-faster-rcnn/blob/master/lib/datasets/voc_eval.py    该代码使用的是方法二。

我看网上关于如何使用该代码并没有做出解释，我这里用voc中的几张图片计算了一下map（自己算法的测试结果，比如说对voc中的cat类，就新建一个cat.txt，其中存储“图片名 矩形框坐标”格式的信息），具体文件在链接：https://pan.baidu.com/s/1336g7ccc4gZ2EKNu9PNndQ 提取码：57yd  中，大家有需要的可以按照这个里面的格式来操作该代码计算map。

AUC和MAP之间的联系：

AUC主要考察模型对正样本以及负样本的覆盖能力（即“找的全”），而MAP主要考察模型对正样本的覆盖能力以及识别能力（即对正样本的“找的全”和“找的对”）