再谈Lasso回归 | elastic net | Ridge Regression

前文：Lasso linear model实例 | Proliferation index | 评估单细胞的增殖指数

参考：LASSO回歸在生物醫學資料中的簡單實例 - 生信技能树

Linear least squares, Lasso,ridge regression有何本质区别？

你应该掌握的七种回归技术 （好文，解释了各个回归的特点，以及分别应用在什么场合）

热门数据挖掘模型应用入门（一）: LASSO 回归 - 侯澄钧

Feature Selection using LASSO - 原文论文  （英文的讲解更全面，更好理解，强烈推荐阅读）

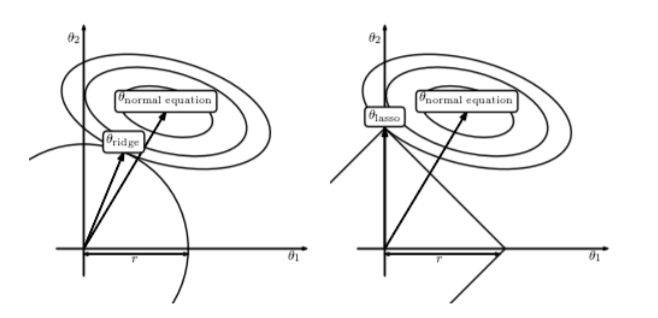
这幅图解释了为什么LASSO会让大部分的β_j(λ) = 0

假设一个二维模型对应的系数是 β1 和 β2，然后 β 是最小化误差平方和的点， 即用传统线性回归得到的自变量系数。 但我们想让这个系数点必须落在蓝色的正方形内，所以就有了一系列围绕 β 的同心椭圆， 其中最先与蓝色正方形接触的点，就是符合约束同时最小化误差平方和的点。

两篇经典文章：

Prediction of clinical outcome in glioblastoma using a biologically relevant nine-microRNA signature

Reconstruction of enhancer–target networks in 935 samples of human primary cells, tissues and cell lines

回归中的多重共线性 Multicollinearity

elastic net

sklearn.linear_model.LassoCV  Python API

常识：

||w||_2: ||w||带一个下标2 的意思是这个该向量的范数为欧几里得范数，设w=<x1,x2,x3>, ||w||_2=x1^2+x2^2+x3^2 的开根号。
(||w||_2)^2 的意思是w的欧几里得范数的平方，也就是(||w||_2)^2=x1^2+x2^2+x3^2

ŷ：y的估计值

arg min 就是使后面这个式子达到最小值时的变量的取值

---

今天经同学指点才发现自己的认知问题，豁然开朗！！

在python sklearn里，L1就是Lasso，L2就是ridge！

所以Lasso就像是贝叶斯一样，只是附加到基础模型上的东西。

Is regression with L1 regularization the same as Lasso, and with L2 regularization the same as ridge regression? And how to write “Lasso”?

待续~