B. Irreducible Anagrams【CF 1290B】

思路：

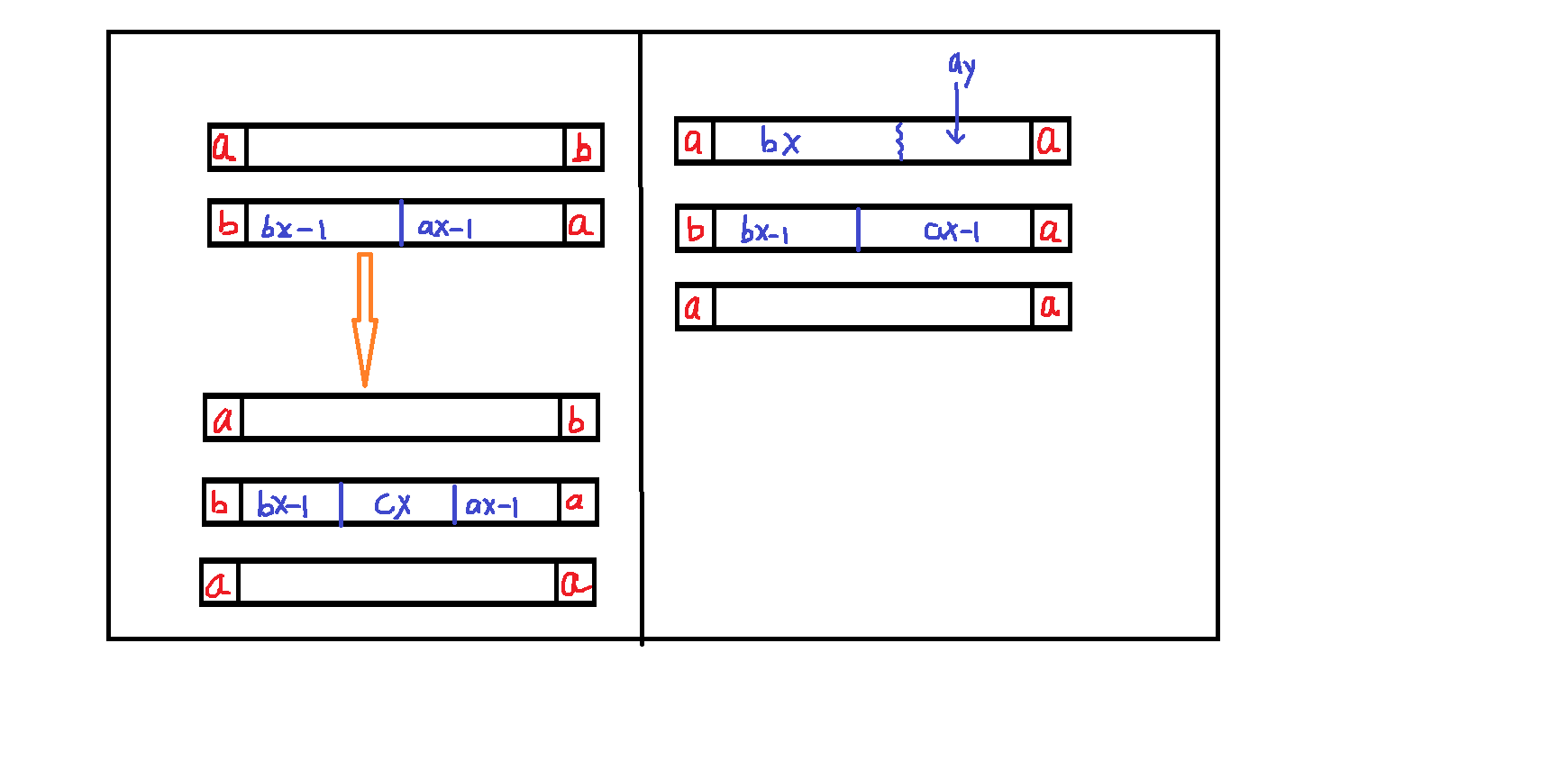
设tx为t类别字符的个数。

①对于长度小于2的t明显是"YES"
②对于字符类别只有1个的t明显是"YES"
③对于字符类别有2个的t，如左上图：如果str[l] != str[r],那么我们构造的t也应该是str[l] != str[r]，且s字串和t的str[l]和str[r]是相反的，即如图所示。继续，如图构造，即bbb..a...a这样，我们发现第一个图片除去str[l] = a和str[r]=b之外，中间怎么放置字符，都会出现"Irreducible Anagrams"的情况，所以"YES"。
④对于字符类别有2个的t，如果str[l] == str[r]，如右边的图，总有k = 2，让s1包含一个a和bx个b,使得"reducible Anagrams"存在,所以"NO"。
④对于字符类别有3个的t，按着左上的图也无法构造出"Irreducible Anagrams" 情况，说明字符类别为3的t，不论说明字符排列都存在"reducible Anagrams",所以"NO"。
⑤对于字符类别大于3个的t，由④推出是"NO"。

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <algorithm>
 4 #include <cstring>
 5 using namespace std;
 6
 7 const int N = 2e5 + 10;
 8 int dp[30][N];
 9 char str[N];
10
11 void solve()
12 {
13     scanf("%s", str);
14     int n = strlen(str);
15   ///  cout << "n = " << n << endl;
16     for(int i = 1; i <= n; ++i) {
17         dp[str[i - 1] - 'a'][i]++;
18      ///   cout << dp[str[i - 1] - 'a'][i] << endl;
19         for(int c = 0; c < 26; ++c) {
20             dp[c][i] += dp[c][i - 1];
21         }
22     }
23 /*
24     for(int c = 0; c < 26; ++c) {
25         printf("%c :\n", 'a' + c);
26         for(int i = 1; i <= n; ++i) {
27             printf("%d ", dp[c][i]);
28         }
29         printf("\n");
30     }
31 */
32     int q;
33     scanf("%d", &q);
34     vector<pair<int ,int > > vp;
35     for(int i = 0; i < q; ++i) {
36         int l, r;
37         scanf("%d%d", &l, &r);
38         vp.push_back(make_pair(l, r));
39     }
40
41     ///vector<int > ans;
42     for(auto info : vp) {
43         int l = info.first;
44         int r = info.second;
45
46         int kinds = 0;
47         int sum = 0;
48         for(int c = 0; c < 26; ++c) {
49             kinds += (dp[c][r] - dp[c][l - 1]) > 0;
50             sum += dp[c][r] - dp[c][l - 1];
51         }
52         ///cout << "tot = " << kinds << endl;
53         if(sum == 1 || (kinds == 2 && str[l - 1] != str[r - 1]) || kinds > 2) {
54             printf("YES\n");
55         } else printf("NO\n");
56     }
57
58 }
59
60 int main()
61 {
62     solve();
63
64     return 0;
65 }