leetcode 63 不同路径II
二维数组动态规划,还可以采用一维数组进行动态规划。
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m=obstacleGrid.size(),n=obstacleGrid[].size();
if(m== ||n==) return ;
long dp[m][n];
if(obstacleGrid[m-][n-]==) return ;
dp[m-][n-]=;
for(int j=n-;j>=;j--){
dp[m-][j]=dp[m-][j+]*(-obstacleGrid[m-][j]);
}
for(int i=m-;i>=;i--){
dp[i][n-]=dp[i+][n-]*(-obstacleGrid[i][n-]);
}
for(int i=m-;i>=;i--){
for(int j=n-;j>=;j--){
dp[i][j]=(-obstacleGrid[i][j])*dp[i+][j]+(-obstacleGrid[i][j])*dp[i][j+];
}
}
return dp[][];
}
};
leetcode 63 不同路径II的更多相关文章
- Java实现 LeetCode 63 不同路径 II(二)
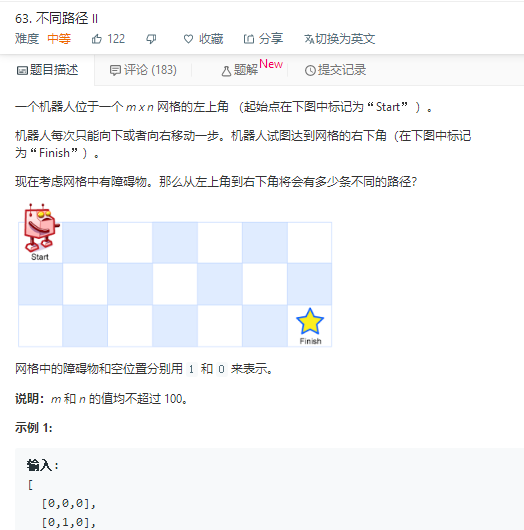
63. 不同路径 II 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为"Start" ). 机器人每次只能向下或者向右移动一步.机器人试图达到网格的右下角(在 ...
- [LeetCode] 63. 不同路径 II ☆☆☆(动态规划)
描述 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” ). 机器人每次只能向下或者向右移动一步.机器人试图达到网格的右下角(在下图中标记为“Finish”). 现在 ...
- LeetCode 63. 不同路径 II(Unique Paths II)
题目描述 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” ). 机器人每次只能向下或者向右移动一步.机器人试图达到网格的右下角(在下图中标记为“Finish”). ...
- Leetcode之动态规划(DP)专题-63. 不同路径 II(Unique Paths II)
Leetcode之动态规划(DP)专题-63. 不同路径 II(Unique Paths II) 初级题目:Leetcode之动态规划(DP)专题-62. 不同路径(Unique Paths) 一个机 ...
- 刷题-力扣-63. 不同路径 II
63. 不同路径 II 题目链接 来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/unique-paths-ii/ 著作权归领扣网络所有.商业转 ...
- 63.不同路径II
目录 63.不同路径Ⅱ 题目 题解 63.不同路径Ⅱ 题目 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为"Start" ). 机器人每次只能向下或者向右移动 ...
- [LeetCode] 63. Unique Paths II 不同的路径之二
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below). The ...
- LeetCode 63. Unique Paths II不同路径 II (C++/Java)
题目: A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below). ...
- LeetCode 63. Unique Path II(所有不同路径之二)
Follow up for "Unique Paths": Now consider if some obstacles are added to the grids. How m ...
随机推荐
- 前端开发 | 尝试用Markdown写一下近几个月的总结
近期总结 回顾 半年前 半年前,接触了前端一年多(工作半年)的我了解的东西只有下面这些.因为在公司里的工作就是切静态页,捣鼓CMS. HTML (比较简洁的编写HTML) CSS/CSS3 (PC兼容 ...
- 使用QEMU模拟树莓派
QEMU上的树莓派 我们开始设置一个Lab VM.我们将使用Ubuntu并在其中模拟我们所需的ARM版本. 首先,获取最新的Ubuntu版本并在VM中运行它: https://www.ubuntu.c ...
- 2019-2020-1 20199319《Linux内核原理与分析》第九周作业
进程的切换和系统的一般执行过程 进程调度的时机 1.中断:起到切出进程指令流的作用.中断处理程序是与进程无关的内核指令流.中断类型: 硬中断:可屏蔽中断和不可屏蔽中断.高电平说明有中断请求. 软中断/ ...
- linux centos 7安装 apache php 及mariadb
1安装Apache, PHP, MySQL以及php库组件. yum -y install httpd php mysql php-mysql 2 安装apache扩展 yum -y install ...
- fiddler获取响应时间以及服务器IP
抓包工具fiddler实现http协议请求应答抓包.在接口测试.性能测试.安全测试等软件测试活动过程中,可能会遇到需要获取接口响应时间.接口服务器IP这样的情况.默认情况下fiddler不支持接口响应 ...
- .net Core的例子
阅读文章: 十二个 ASP.NET Core 例子
- Python基于机器学习方法实现的电影推荐系统
推荐算法在互联网行业的应用非常广泛,今日头条.美团点评等都有个性化推荐,推荐算法抽象来讲,是一种对于内容满意度的拟合函数,涉及到用户特征和内容特征,作为模型训练所需维度的两大来源,而点击率,页面停留时 ...
- 简述Hibernate常见优化策略
①制定合理的缓存策略 ② 采用合理的Session管理机制 ③ 尽量使用延迟加载特性 ④如果可以, 选用基于version的乐观锁替代悲观锁 ⑤在开发过程中, 开启hibernate.show_sql ...
- FM算法详解
https://blog.csdn.net/jediael_lu/article/details/77772565 https://blog.csdn.net/bitcarmanlee/article ...
- C# 跨窗体事件
跨窗体事件:例如从一个窗体改变另一个窗体button的颜色,首先需要将需要改变button的属性改为public using System; using System.Drawing; using S ...
