洛谷p1149

一道很有意思的题目嘞。



这道题目看起来，用搜索似乎无疑了。

我想了这样一个办法(看了很多博客似乎都没用这种方法)，可能是觉得太麻烦了吧:

1、我们先把0到9的数字排列，找出排列消耗火柴等于0的序列。这就是dfs函数的作用。

2、将找出的序列传入check函数中，枚举第一个数的长度，在枚举第二个数的长度，然后检查a+b是否等于c。

3、关键是，要满足非个位数不能为0，就是这个语句了。



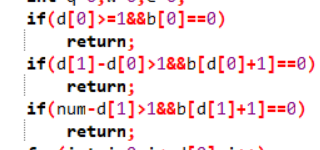
其中d[0]记录第一个数的长度，d[1]记录第二个数的长度，num表示序列总长度。

代码如下:

#include <bits/stdc++.h>
using namespace std;
int a[13]={6,2,5,5,4,5,6,3,7,6};
int b[100],d[4];//数组b储存序列，数组d储存第
一个数和第二个数的长度
int n,sumn=0;
void check(int num,int pos,int gg)//num为从dfs传来的序列长度，上一个数的长度截止到pos，gg表示已经匹配的数-1。
{
	if(gg==2)
	{
		int q=0,w=0,e=0;
		if(d[0]>=1&&b[0]==0)
			return;
		if(d[1]-d[0]>1&&b[d[0]+1]==0)
			return;
		if(num-d[1]>1&&b[d[1]+1]==0)
			return;
		for(int i=0;i<=d[0];i++)
			q=q*10+b[i];
		for(int i=d[0]+1;i<=d[1];i++)
			w=w*10+b[i];
		for(int i=d[1]+1;i<=num;i++)
			e=e*10+b[i];
		if(q+w==e)
		{
			sumn++;
		}
		return;
	}
	for(int i=pos;i<num;i++)
	{
		d[gg]=i;
		check(num,i+1,gg+1);
		d[gg]=0;
	}
}
void dfs(int n,int num)
{
	if(n==0)
	{
		check(num-1,0,0);
		return;
	}
	if(n<2)
		return;
	for(int i=0;i<=9;i++)
	{
		if(n>=a[i])
		{
			b[num]=i;
			dfs(n-a[i],num+1);
			b[num]=0;
		}
	}
}
int main()
{
	cin>>n;
	sumn=0;
	dfs(n-4,0);
	cout<<sumn<<endl;
}

当然，递归写法还有一种，我给个链接大家自己看吧，

纯递归写法

但是，这题有更简单的方法。

我们直接从用两个for循环枚举a和b



其中cal为计算数字需要消耗的火柴数目。为什么上限取到1111呢？题目中火柴只有24根，可用的只有20根。1111需要8根火柴，0需要5根，若满足a+b=c,c也为1111，这里加起来21根。所以在范围内，我们都可以枚举到。

代码:

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int num[11] = {6,2,5,5,4,5,6,3,7,6},n,ans = 0;
int find3(int x)
{
    if(x == 0)
        return 6;
    int an = 0;
    while(x)
    {
        an += num[x % 10];
        x /= 10;
    }
    return an;
}
void find2(int cnt,int a,int x,int k)//第二位数；
{
    if(find3(a + x) == cnt)
        ans ++;
    if(k)//避免首位数为0；
        for(int i = 0;i <= 9;i ++)
        {
            if(cnt - num[i] >= 2)//至少还要放1个1；
                find2(cnt - num[i],a,x * 10 + i,1);
        }
}
void find(int cnt,int x,int k)//第一位数；
{
    for(int i = 0;i <= 9;i ++)
        if(n - num[i] >= 2)
            find2(cnt - num[i],x,i,i);
    if(k)//避免首位数为0；
        for(int i = 0;i <= 9;i ++)
        {
            if(cnt - num[i] >= 4)
                find(cnt - num[i],x * 10 + i,1);
        }
}
int main()
{
    scanf("%d",&n);
    n -= 4;// ‘+’ 和 ‘=’；
    for(int i = 0;i <= 9;i ++)
        if(n - num[i] >= 4)//至少还要放2个1；
            find(n - num[i],i,i);
    printf("%d",ans);
}