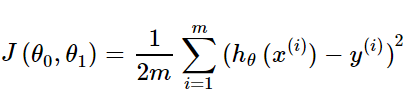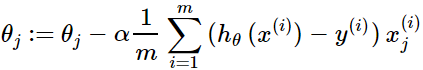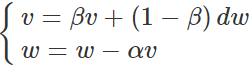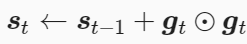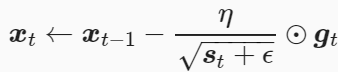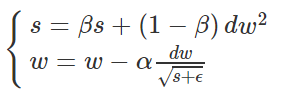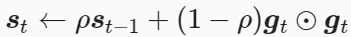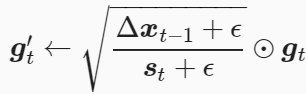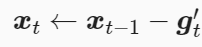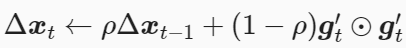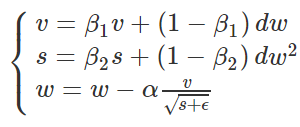【NLP】常用优化方法

1.梯度下降法

　　梯度下降法可以分为三种，批量梯度下降法（BGD）、小批量梯度下降（MBGD）、随机梯度下降法（SGD），这三种方法是优化时对数据所采取的的策略，但所运用的思想是一致的，都是梯度下降，现在先讲解下梯度下降。

　　假设有一目标函数y =x²,对这一凸函数希望寻找到其最小值，这里可以轻松得到梯度为2x，我们假设学习率eta=0.1，每次自变量的变化为eta*2x，既然是梯度下降，那么可得到x = x-eta*2x，代码如下：

import numpy as np

import math

import matplotlib.pyplot as plt

%matplotlib inline

#y=x**2

def gd(eta):

    x =10

    res = [x]

    for i in range(10):

        x -= eta*2*x

        res.append(x)

    return res

res = gd(0.1)

def show_trace(res):

    n = max(abs(min(res)), abs(max(res)), 10)

    f_line = np.arange(-n, n, 0.1)

#     plt.set_figsize()

    plt.plot(f_line, [x * x for x in f_line])

    plt.plot(res, [x * x for x in res], '-o')

    plt.xlabel('x')

    plt.ylabel('f(x)')

show_trace(res)

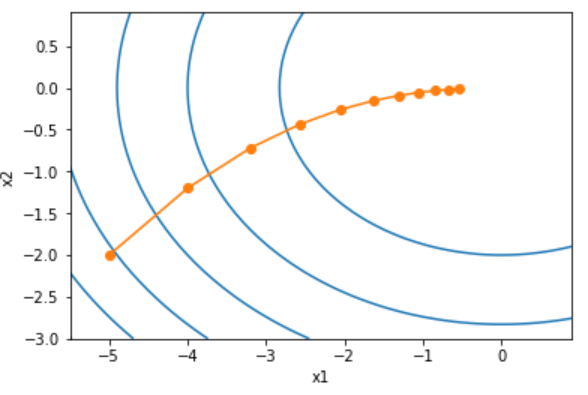
　　迭代10次后结果入下图：

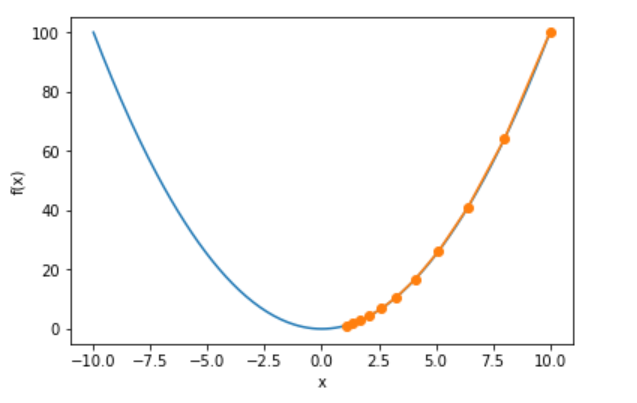
　　可见y随着梯度一步步向最小值优化，这个就是梯度下降的核心，对于多元的也是如此，例如y=x1²+2x2²，见下图，其他形式的变种也是在这个的基础上进行改进，下面开始介绍三种下降方法。

　　为便于理解，我们假定进行线性回归拟合，设函数为

h_θ (x⁽ⁱ⁾) = θ₁x⁽ⁱ⁾+ θ₀其中i = 1,2,3,...m 代表样本数

　　对应的损失函数为

（1）批量梯度下降（Batch Gradient Descent，BGD）

　　BGD是指每次迭代时用所用样本数据计算梯度，

对目标函数求偏导,其中 i=1,2,...,m 表示样本数， j=0,1 表示特征数。

每次迭代对参数进行更新

优点：

　　1.每次计算运用所有数据进行运算，可用矩阵实现并行计算

　　2.通过所有数据求梯度在全局范围进行搜索，当目标函数为凸函数时，一定能达到全局最优

缺点：

　　1.每次求梯度用全部数据会导致训练速度缓慢

（2）随机梯度下降（Stochastic Gradient Descent，SGD）

　　随机梯度下降与批量梯度下降最大的不同在于前者每次计算梯度只采用一个随机样本，即m=1，公式中无求和符号

优点：
1.由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。
缺点：
1.准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
2.可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。
3.不易于并行实现。

　　解释下为什么SGD比BGD迭代更快，假如有100w条数据，BGD一次迭代需要计算100w个样本，可能迭代10次后才能达到全局最优，那么就计算了1000w次梯度；要换成SGD每次随机一个样本，100w条数据迭代完后就可能找到了最优解，此时的计算时间是远小于BGD的。

（3）小批量梯度下降（Mini-Batch Gradient Descent，MBGD）

　　结合BGD和SGD的优缺点，从而衍生出了小批量梯度下降法，跟批量梯度下降很相似，他们的差别在于m=batch，每次随机更新batch个样本数据的梯度，当batch为1时就为SGD，当batch为样本数总数N时即为BGD

优点：
1.通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
2.每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。(比如上例中的100W，设置batch_size=100时，需要迭代1w次，远小于SGD的100w次)
3.可实现并行化。
缺点：
1.batch_size的不当选择可能会带来一些问题。

batch_size的选择带来的影响：
（1）在合理地范围内，增大batch_size的好处：
a. 内存利用率提高了，大矩阵乘法的并行化效率提高。
b. 跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
c. 在一定范围内，一般来说 Batch_Size 越大，其确定的下降方向越准，引起训练震荡越小。
（2）盲目增大batch_size的坏处：
a. 内存利用率提高了，但是内存容量可能撑不住了。
b. 跑完一次 epoch（全数据集）所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加了，从而对参数的修正也就显得更加缓慢。
c. Batch_Size 增大到一定程度，其确定的下降方向已经基本不再变化。

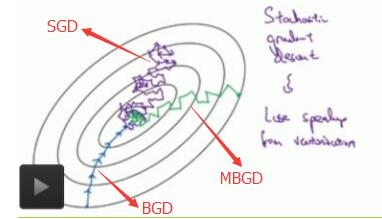
下图为三种迭代策略下目标函数的收敛过程

2.动量法(Momentum)

　　动量法又称冲量算法，其核心思想可看成指数平均，每次求得梯度后都跟前面的梯度进行指数平滑，让梯度更加平滑去防止梯度变化过大，公式如下：

　　d⁢w是我们计算出来的原始梯度，v则是用指数加权平均计算出来的梯度，α为学习率。这相当于对原始梯度做了一个平滑，然后再用来做梯度下降，对于二元函数迭代代码如下：

def momentum_2d(x1, x2, v1, v2):

    v1 = gamma * v1 + (1-gamma)*0.2 * x1

    v2 = gamma * v2 + (1-gamma)*4 * x2

    return x1 - eta * v1, x2 - eta * v2, v1, v2

3.AdaGrad算法

　　AdaGrad算法会使用一个小批量随机梯度g_t按元素平方的累加变量s_t，然后更新的梯度为g_t除以s_t+ε的开方，η为学习率，ϵ是为了维持数值稳定性而添加的常数，如10^-6，具体公式如下：

　　由于s_t会一直累积增大（公式中分母变大），实际可以看成学习率η随机训练而减小，当学习率在迭代早期降得较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，自变量的迭代轨迹较平滑，可能较难找到一个有用的解，对于二元函数迭代代码如下：

def adagrad_2d(x1, x2, s1, s2):

    g1, g2, eps = 0.2 * x1, 4 * x2, 1e-6  # 前两项为自变量梯度

    s1 += g1 ** 2

    s2 += g2 ** 2

    x1 -= eta / math.sqrt(s1 + eps) * g1

    x2 -= eta / math.sqrt(s2 + eps) * g2

    return x1, x2, s1, s2

4.RMSProP算法

　　RMSProP算法可以看成AdaGrad算法的改进，在AdaGrad的基础上加上Momentum法，第一步不再是直接加和，而是引入指数平滑，对每一次的平方和进行平滑，RMSprop迭代更新公式如下：

　　β的典型值是0.999。公式中还有一个ϵ，这是一个很小的数，典型值是10^-8。对于二元函数迭代代码如下：

def rmsprop_2d(x1, x2, s1, s2):

    g1, g2, eps = 0.2 * x1, 4 * x2, 1e-6

    s1 = gamma * s1 + (1 - gamma) * g1 ** 2

    s2 = gamma * s2 + (1 - gamma) * g2 ** 2

    x1 -= eta / math.sqrt(s1 + eps) * g1

    x2 -= eta / math.sqrt(s2 + eps) * g2

    return x1, x2, s1, s2

5.AdaDelta算法

　　AdaDelta算法同样是在AdaGrad算法进行改进，有意思的是，AdaDelta算法没有学习率这一超参数，

　　(1)梯度平方求和并加入指数平滑

　　(2)AdaDelta算法还维护一个额外的状态变量Δx_t，其元素同样在时间步0时被初始化为0。我们使用Δx_t-1来计算自变量的变化量

　　(3)其中ϵ是为了维持数值稳定性而添加的常数，如10^-5。接着更新自变量

　　(4)最后，我们使用Δx_t来记录自变量变化量g′_t按元素平方的指数加权移动平均

　　可以看到，如不考虑ϵ的影响，AdaDelta算法与RMSProp算法的不同之处在于使用√Δxt−1来替代超参数η。

6.Adam算法

Adam算法则是RMSProP算法和Momentum法的结合。先看迭代更新公式：

分母部分取的是RMSProP算法，分子部分取的是Momentum法，典型值：β1=0.9,β2=0.999,ϵ=10−8◂,▸β1=0.9,β2=0.999,ϵ=10−8。Adam算法相当于先把原始梯度做一个指数加权平均，再做一次归一化处理，然后再更新梯度值。

引用及参考

http://zh.gluon.ai/chapter_optimization/optimization-intro.html

https://www.cnblogs.com/lliuye/p/9451903.html

https://www.cnblogs.com/jiaxblog/p/9695042.html