Canvas画椭圆的方法

虽然标题是画椭圆，但是我们先来说说Canvas中的圆

相信大家对于Canvas画圆都不陌生

 

oGC.arc(400, 300, 100, 0, 2*Math.PI, false);

如上所示，直接调用API就可以了，但是计算机内部却是使用光栅学，利用bresenham算法画圆的，这个我们放到最后来说，先说说利用圆的参数方程画圆

circle(oGC, 400, 300, 100);
function circle(context, x, y, a) { // x,y是坐标;a是半径
    var r = 1/a; // ①注意：此处r可以写死，不过不同情况下写死的值不同
    context.beginPath();
    context.moveTo(x + a, y);
    for(var i = 0; i < 2 * Math.PI; i += r) {
        context.lineTo(x + a * Math.cos(i), y + a * Math.sin(i));
    }
    context.closePath();
    context.fill();
}

 

原理是什么，相信三角函数不错的童鞋理解起来很容易的，如果不知道的话，注意注释①，我变化一下r的值，相信就立竿见影了~

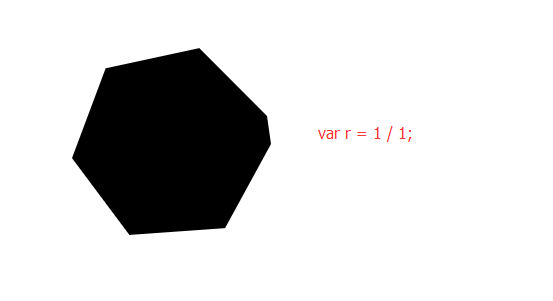
r和2*Math.PI配合就是圆的精细程度，在半径为100的时候，r取1/10就可以了，通用的话可以写死，写成r = 1 / a；这样无论半径取大或者小，圆都会很精细，但是性能会有很大影响

现在来看看文章的主角，针对圆来看椭圆的

function EllipseOne(context, x, y, a, b) {
    var step = (a > b) ? 1 / a : 1 / b;
    context.beginPath();
    context.moveTo(x + a, y);
    for(var i = 0; i < 2 * Math.PI; i += step) {
        context.lineTo(x + a * Math.cos(i), y + b * Math.sin(i));
    }
    context.closePath();
    context.fill();
}

和圆基本一样，不过圆只有一个半径，而椭圆分为长轴和短轴了。

看下效果~

好了，画椭圆成功，文章结束~

怎么可能！！

就这样结束也太没品了，刚刚是方法一，下面来看其他的

方法二，均匀压缩法

这是我最喜欢的方法，易理解，相比较方法一，性能也快了很多，先贴代码~

function EllipseTwo(context, x, y, a, b) {
    context.save();
    var r = (a > b) ? a : b;
    var ratioX = a / r;
    var ratioY = b / r;
    context.scale(ratioX, ratioY);
    context.beginPath();
    context.arc(x / ratioX, y / ratioY, r, 0, 2 * Math.PI, false);
    context.closePath();
    context.restore();
    context.fill();
}

原理是利用了scale来对一个标准的圆进行压缩，ratioX是横轴缩放比率，ratioY是纵轴缩放比率，就因为这两个值不同，使得将标准圆缩放成了一个椭圆

记得save()和restore()还原context环境，so easy理解的方法

下面两种方法很高大上，都是利用三次贝塞尔曲线法

方法三，四，贝塞尔法

function EllipseThree(context, x, y, a, b) {
    var ox = 0.5 * a,
        oy = 0.6 * b;

    context.save();
    context.translate(x, y);
    context.beginPath();
    context.moveTo(0, b);
    context.bezierCurveTo(ox, b, a, oy, a, 0);
    context.bezierCurveTo(a, -oy, ox, -b, 0, -b);
    context.bezierCurveTo(-ox, -b, -a, -oy, -a, 0);
    context.bezierCurveTo(-a, oy, -ox, b, 0, b);
    context.closePath();
    context.fill();
    context.restore();
}

function EllipseFour(context, x, y, a, b) {
    var k = 0.5522848,
    ox = k * a,
    oy = k * b;

    context.translate(x, y);
    context.beginPath();
    context.moveTo(-a, 0);
    context.bezierCurveTo(-a, oy, -ox, -b, 0, -b);
    context.bezierCurveTo(ox, -b, a, -oy, a, 0);
    context.bezierCurveTo(a, oy, ox, b, 0, b);
    context.bezierCurveTo(-ox, b, -a, oy, -a, 0);
    context.closePath();
    context.fill();
}

贝塞尔法的核心在于两个控制点的选取，但是它有致命的问题，当lineWidth较宽的时候，椭圆较扁，长轴较尖锐，会出现不平滑的情况

如果不知道什么事贝塞尔的话就自行百度……这个不解释了……

后面还有最后一种光栅法画椭圆，光栅法画圆很简单，画椭圆挺麻烦的，下面是最简单的一种椭圆画法，等于是lineWidth为1px的情况下

function EllipseFive(context, x, y, a, b) {
    var data = context.getImageData(0, 0, 800, 600);
    var imageData = data.data;
    var tx = 0;
    var ty = b;
    var d = b*b + a*a*(-b + 0.25);
    var mx = a * a / Math.sqrt(a * a + b * b);

    while(tx <= mx) {
        if(d < 0) {
            d += b * b * (2 * tx + 3);
        } else {
            ty--;
            d += b * b * (2 * tx + 3) + 2 * a * a * (1 - ty);

        }

        tx++;
        setPix(x + tx, y + ty);
        setPix(x + tx, y - ty);
        setPix(x - tx, y + ty);
        setPix(x - tx, y - ty);
    }

    d = b * b * (tx + 0.5) * (tx + 0.5) + a * a * (ty - 1) * (ty - 1) - a * a * b * b;
    while (ty > 0) {
        if (d < 0) {
            tx++;
            d += b*b*(2 * tx + 2) + a*a*(-2 * ty + 3);
        }
        else {
            d += a*a*(-2 * ty + 3);
        }
        ty--;
        setPix(x + tx, y + ty);
        setPix(x - tx, y + ty);
        setPix(x + tx, y - ty);
        setPix(x - tx, y - ty);
    }

    context.putImageData(data, 0, 0);

    function setPix(x, y){
        console.log(x, y);
        var index = getStartIndex(x, y);
        for(var i = 0; i< 4; i++) {
            if(i == 3) {
                imageData[index + i] = 255;
            }
            else{
                imageData[index + i] = 128;
            }
        }
    }

    function getStartIndex(x, y) {
        return y * 800 * 4 + x * 4;
    }
}

给个结果图~

光栅法的原理在这里就不说啦，那个说的话篇幅很大，在这里也不推荐用光栅法去画椭圆，针对不同线宽很麻烦

ok这篇文章就到这啦，Thanks~

 

原创文章转载请注明：

转载自AlloyTeam：http://www.alloyteam.com/2015/07/canvas-hua-tuo-yuan-di-fang-fa/