洛谷 P2486 BZOJ 2243 [SDOI2011]染色

题目描述

给定一棵有n个节点的无根树和m个操作，操作有2类：

1、将节点a到节点b路径上所有点都染成颜色c；

2、询问节点a到节点b路径上的颜色段数量（连续相同颜色被认为是同一段），如“112221”由3段组成：“11”、“222”和“1”。

请你写一个程序依次完成这m个操作。

输入输出格式

输入格式：

第一行包含2个整数n和m，分别表示节点数和操作数；

第二行包含n个正整数表示n个节点的初始颜色

下面 行每行包含两个整数x和y，表示x和y之间有一条无向边。

下面 行每行描述一个操作：

“C a b c”表示这是一个染色操作，把节点a到节点b路径上所有点（包括a和b）都染成颜色c；

“Q a b”表示这是一个询问操作，询问节点a到节点b（包括a和b）路径上的颜色段数量。

输出格式：

对于每个询问操作，输出一行答案。

输入输出样例

输入样例#1：

6 5
2 2 1 2 1 1
1 2
1 3
2 4
2 5
2 6
Q 3 5
C 2 1 1
Q 3 5
C 5 1 2
Q 3 5

输出样例#1：

3
1
2

说明

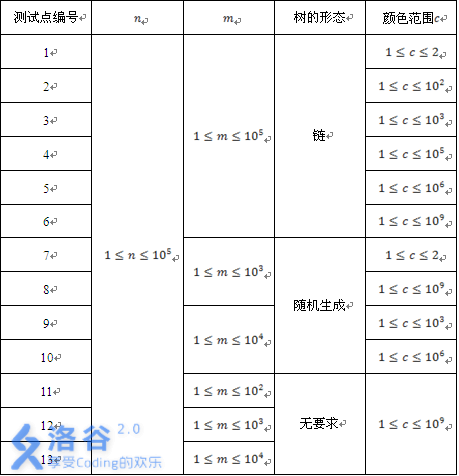
//这个题面一半来自洛谷，一半来自BZOJ

解题思路

　　树剖套线段树。这题重点在线段树上。线段树的每个节点存下此节点表示的区间范围l、r，这个区间内颜色块数num，l处的颜色lc，r处的颜色rc。

　　然后从合并两个区间的信息时，特判如果接口处颜色相同，则当前区间num等于两个子区间num之和减一，不相等就不减一(语文不好，勉强看吧)

源代码

#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>

int n,m;

struct Edge{
    int next,to;
}e[];
int head[]={},cnt=;
void add(int u,int v)
{
    e[cnt]={head[u],v};
    head[u]=cnt++;
}
int color[]={};
struct tree{
    int fa;
    int w;
    int dep;
    int num_to;
    int wson;
    int top;
    int id;
}t[];

void dfs1(int fa,int u,int dep)
{
    t[u].fa=fa;
    t[u].dep=dep;
    t[u].num_to=;
    t[u].wson=-;
    int max_to=,num_son=;
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(v==fa) continue;
        num_son++;
        dfs1(u,v,dep+);
        int temp=t[v].num_to;
        t[u].num_to+=temp;
        if(temp>max_to) t[u].wson=v,max_to=temp;
    }
}
int id=;
void dfs2(int u,int top)
{
    t[u].top=top;
    t[u].id=id;
    color[id]=t[u].w;
    id++;
    if(t[u].wson==-) return;
    dfs2(t[u].wson,top);
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(v==t[u].fa||v==t[u].wson) continue;
        dfs2(v,v);
    }
}

struct stree{
    int l,r;
    int lc,rc;//边界l、r的颜色
    int num;//区间内色块数
}s[];
int lazy[]={};//区间染色lazy
void maketree(int x,int l,int r)
{
    s[x].l=l,s[x].r=r;
    s[x].lc=color[l],s[x].rc=color[r];
    if(l==r)
    {
        s[x].num=;
        return;
    }
    int mid=l+r>>;
    maketree(x<<,l,mid);
    maketree(x<<|,mid+,r);
    s[x].num=s[x<<].num+s[x<<|].num-(s[x<<].rc==s[x<<|].lc);
}
void pushdown(int x)
{
    int ls=x<<,rs=ls|;
    s[rs].num=s[ls].num=;
    s[ls].lc=s[ls].rc=s[rs].rc=s[rs].lc=lazy[ls]=lazy[rs]=lazy[x];
    lazy[x]=;
}
int query(int x,int l,int r)
{
    if(l>s[x].r||r<s[x].l) return ;
    if(l<=s[x].l&&s[x].r<=r) return s[x].num;
    if(lazy[x]) pushdown(x);
    int ans=query(x<<,l,r)+query(x<<|,l,r);
    if(l<=s[x<<].r&&r>=s[x<<|].l&&s[x<<].rc==s[x<<|].lc) ans--;
    return ans;
}
int query_color(int x,int pos)
{
    int l=s[x].l,r=s[x].r;
    if(l==r) return s[x].lc;
    int mid=l+r>>;
    if(lazy[x]) pushdown(x);
    if(pos<=mid) return query_color(x<<,pos);
    else return query_color(x<<|,pos);
}
void update(int x,int l,int r,int c)
{
    if(l>s[x].r||r<s[x].l) return;
    if(l<=s[x].l&&s[x].r<=r)
    {
        lazy[x]=c;
        s[x].num=;
        s[x].lc=s[x].rc=c;
        return;
    }
    if(lazy[x]) pushdown(x);
    update(x<<,l,r,c),update(x<<|,l,r,c);
    s[x].lc=s[x<<].lc;
    s[x].rc=s[x<<|].rc;
    s[x].num=s[x<<].num+s[x<<|].num-(s[x<<].rc==s[x<<|].lc);
}

void C(int x,int y,int c)
{
    while(t[x].top!=t[y].top)
    {
        if(t[t[y].top].dep<t[t[x].top].dep) std::swap(x,y);//y的top更深
        update(,t[t[y].top].id,t[y].id,c);
        y=t[t[y].top].fa;
    }
    if(t[y].id<t[x].id) std::swap(x,y);
    update(,t[x].id,t[y].id,c);
}
int Q(int x,int y)
{
    int ans=;
    while(t[x].top!=t[y].top)
    {
        if(t[t[y].top].dep>t[t[x].top].dep) std::swap(x,y);//x的top更深
        ans+=query(,t[t[x].top].id,t[x].id)-(query_color(,t[t[x].top].id)==query_color(,t[t[t[x].top].fa].id));
        x=t[t[x].top].fa;
    }
    if(t[y].id<t[x].id) std::swap(x,y);
    ans+=query(,t[x].id,t[y].id);
    return ans==?:ans;
}

int main()
{
    //freopen("test.in","r",stdin);
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++) scanf("%d",&t[i].w);
    for(int i=,u,v;i<n;i++)
    {
        scanf("%d%d",&u,&v);
        add(u,v);
        add(v,u);
    }
    dfs1(,,);
    dfs2(,);
    maketree(,,n);
    for(int i=,a,b,c;i<=m;i++)
    {
        char mode[];
        scanf("%s",mode);
        if(mode[]=='Q')
        {
            scanf("%d%d",&a,&b);
            printf("%d\n",Q(a,b));
        }
        else
        {
            scanf("%d%d%d",&a,&b,&c);
            C(a,b,c);
        }
    }
    return ;
}