POJ 1186 方程的解数

方程的解数

Time Limit: 15000MS		Memory Limit: 128000K
Total Submissions: 6188		Accepted: 2127
Case Time Limit: 5000MS

Description

已知一个n元高次方程： 
 
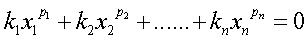
其中：x1, x2,...,xn是未知数，k1,k2,...,kn是系数，p1,p2,...pn是指数。且方程中的所有数均为整数。 
假设未知数1 <= xi <= M, i=1,,,n，求这个方程的整数解的个数。 
1 <= n <= 6；1 <= M <= 150。 
 
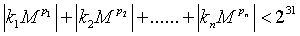
方程的整数解的个数小于2³¹。 
★本题中，指数Pi(i=1,2,...,n)均为正整数。 

Input

第1行包含一个整数n。第2行包含一个整数M。第3行到第n+2行，每行包含两个整数，分别表示ki和pi。两个整数之间用一个空格隔开。第3行的数据对应i=1，第n+2行的数据对应i=n。

Output

仅一行，包含一个整数，表示方程的整数解的个数。

Sample Input

3
150
1  2
-1  2
1  2

Sample Output

178

#include<stdio.h>
#include<stdlib.h>
#define Max 4000037
int hash[Max],num[Max];
//hash判断和的位置，num是和为s的个数 bool used[Max];
bool used[Max];
//判断hash是否用过
int n,M,k[],p[],cnt,mid;
int locat(int s)
{
    int tmp=s;
    while(tmp<)
    {
        tmp+=Max;
    }
    while(tmp>=Max)
    {
        tmp-=Max;
    }
    while(used[tmp]&&hash[tmp]!=s)
    {
        tmp++;
        if(tmp>=Max)
        {
            tmp-=Max;
        }
    }
    return tmp;
}  

void in_sert(int s)
{
    int pos=locat(s);
    hash[pos]=s;
    used[pos]=;
    num[pos]++;
}
void left_dfs(int d,int s)          //左边一半的值的和的可能
{
    if(d==mid)
    {
        in_sert(s);
        return  ;
    }
    for(int i=;i<=M;i++)
    {
        int tmp=k[d];
        if(i!=&&tmp!=)
        {
            for(int j=;j<p[d];j++)
            {
                tmp*=i;
            }
        }
        left_dfs(d+,s+tmp);
    }
}  

void right_dfs(int d,int s)        //右边所有和的可能如果左右相等，那么就加上这个和的所有可能
{
    if(d==n)
    {
        s=-s;
        int pos=locat(s);
        if(hash[pos]==s)
        {
            cnt+=num[pos];
        }
        return ;
    }
    for(int i=;i<=M;i++)
    {
        int tmp=k[d];
        if(i!=&&tmp!=)
        {
            for(int j=;j<p[d];j++)
            {
                tmp*=i;
            }
        }
        right_dfs(d+,s+tmp);
    }
}
int main()
{
    int i,j;
    scanf("%d",&n);
    scanf("%d",&M);
    for(i=;i<n;i++)
    {
        scanf("%d%d",&k[i],&p[i]);
    }
    mid=n/;
    cnt=;
    left_dfs(,);
    right_dfs(mid,);
    printf("%d\n",cnt);
    return ;
}