machine learning (3)---Linear Algebra Review
- Matrix Vector Multiplication
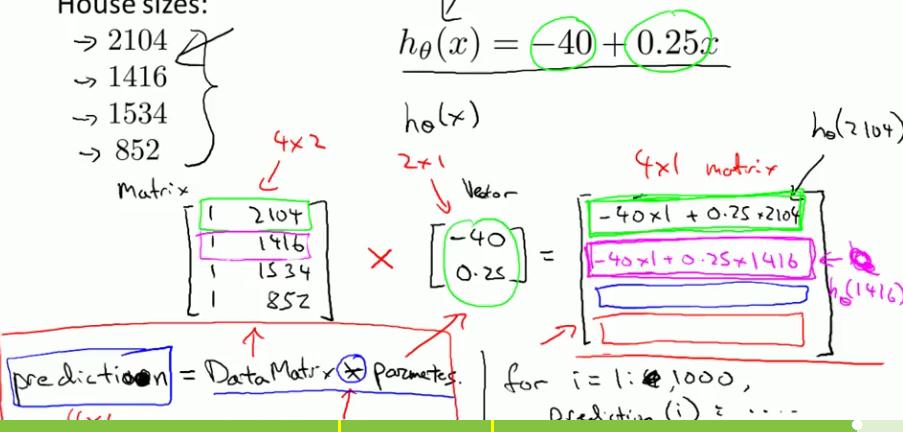
- 左边的矩阵向量相乘法比右边的更简洁而且计算高效
- Matrix Matrix Multiplication

- 可以同时计算12个结果(4个房子面积与3个不同的预测函数),更简洁与高效(利用计算机的并行计算等)
machine learning (3)---Linear Algebra Review的更多相关文章
- Machine learning(3-Linear Algebra Review )
1.Matrices and vectors Matrix :Rectangular array of numbers a notation R3×3 Vector : An n×1 matrix t ...
- ON THE EVOLUTION OF MACHINE LEARNING: FROM LINEAR MODELS TO NEURAL NETWORKS
ON THE EVOLUTION OF MACHINE LEARNING: FROM LINEAR MODELS TO NEURAL NETWORKS We recently interviewed ...
- Machine Learning #Lab1# Linear Regression
Machine Learning Lab1 打算把Andrew Ng教授的#Machine Learning#相关的6个实验一一实现了贴出来- 预计时间长度战线会拉的比較长(毕竟JOS的7级浮屠还没搞 ...
- CheeseZH: Stanford University: Machine Learning Ex1:Linear Regression
(1) How to comput the Cost function in Univirate/Multivariate Linear Regression; (2) How to comput t ...
- machine learning (2)-linear regression with one variable
machine learning- linear regression with one variable(2) Linear regression with one variable = univa ...
- 【Coursera - machine learning】 Linear regression with one variable-quiz
Question 1 Consider the problem of predicting how well a student does in her second year of college/ ...
- 斯坦福第三课:线性代数回顾(Linear Algebra Review)
3.1 矩阵和向量 3.2 加法和标量乘法 3.3 矩阵向量乘法 3.4 矩阵乘法 3.5 矩阵乘法的性质 3.6 逆.转置 3.1 矩阵和向量 如图:这个是 4×2 矩阵,即 4 行 ...
- Ng第三课:线性代数回顾(Linear Algebra Review)
3.1 矩阵和向量 3.2 加法和标量乘法 3.3 矩阵向量乘法 3.4 矩阵乘法 3.5 矩阵乘法的性质 3.6 逆.转置 3.1 矩阵和向量 如图:这个是 4×2 矩阵,即 4 行 ...
- 机器学习第3课:线性代数回顾(Linear Algebra Review)
3.1 矩阵和向量 如图:这个是 4×2 矩阵,即 4 行 2 列,如 m 为行,n 为列,那么 m×n 即 4×2 矩阵的维数即行数×列数 矩阵元素(矩阵项): Aij 指第 i 行,第 j 列的 ...
随机推荐
- 在ensp上VLAN基础配置以及Access接口
什么是VLAN? 早期的局域网技术是基于总线型的结构,也就是说所有主机共享一条传输线路.这就带来了很多问题:冲突域和安全问题.为了避免冲突域,我们使用二层交换机.但想想,一台计算机在总线上传输数据的时 ...
- 卸载桌面产品,弹出错误框The Windows Installer service could not be accessed
卸载程序报这个错误: https://helpdeskgeek.com/how-to/how-to-fix-the-windows-installer-service-could-not-be-acc ...
- gdb调试常用功能
一.gdb中宏定义 macro define list_entry(ptr, type, member) ((type)( (char)ptr - (unsigned long)(&((typ ...
- vim实用操作指南
一.查看文件编码 :set fileencoding :set fileencoding=utf-8 通过该命令可直接将文件修改为UTF-8编码 强制以指定编码打开,vim中 :e ++enc=utf ...
- vue --- axios拦截器+form格式请求体
在vue2.x中使用CLI生成的模板有很大改变,需要自己手动在main.ts同级目录下新建interceptors.ts interceptors.ts import axios from 'axio ...
- PB 奇葩BUG
1. 在数据窗口的Edit 中选则CHeckBox 后,必须给默认值,否则会导致数据保存不了,也无提示. 2.当使用数据窗口的 setfile()函数时 如果 条件中有两个LIKE 则会报错,一个LI ...
- Oracle 11g Java驱动包ojdbc6.jar安装到maven库,并查看jar具体版本号
ojdbc6.jar下载 Oracle官方宣布的Oracle数据库11g的驱动jar包是ojdbc6.jar ojdbc6.jar下载地址:https://www.oracle.com/technet ...
- fastjson框架如何处理boolean?CURRENT_TIMESTAMP使用报错?什么是 ONLINE DDL 及 pt-online-schema-change ? getBytes引起的乱码问题?
一.使用fastjson框架进行序列化时,若莫个参数为Boolean类型,而json里的值是其它类型时,框架如何处理? 1.true, false,正常赋值2.int类型,若为1,则为true,否则为 ...
- Java多线程编程之读写锁【ReentrantReadWriteLock】
有时候我们需要有这样的需求: 对于同一个文件进行读和写操作,普通的锁是互斥的,这样读的时候会加锁,只能单线程的读,我们希望多线程的进行读操作,并且读的时候不能进行写操作,写的时候不能进行 ...
- LOJ3146 APIO2019路灯(cdq分治+树状数组)
每个时刻都形成若干段满足段内任意两点可达.将其视为若干正方形.则查询相当于求历史上某点被正方形包含的时刻数量.并且注意到每个时刻只有O(1)个正方形出现或消失,那么求出每个矩形的出现时间和消失时间,就 ...
