Codeforces Round 978 (Div. 2) A-D1 题解

A. Bus to Pénjamo

题意

有一辆车上面有 \(r\) 排座位，每排有 \(2\) 个座位，现在共 \(n\) 个家庭出行坐公交车，每个家庭 \(a_i\) 个人（保证 \(2r\ge \sum a_i\)）。

一个人感到 开心，当且仅当符合一下条件 之一：

• 他和他的家庭成员坐在一排
• 他独自一人坐在一排（旁边不能有其他人）

问最终最多有多少人 开心

思路

贪心，先让可以两个人一排的家庭成员入座，剩下的看 \([座位数]\) 与 \([剩余人数]\) 的差，得出有多少人能单独坐一排

C++ 代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,r;
void solve(){
	cin>>n>>r;
	int k=0;
	int ans=0;
	for(int i=0;i<n;i++){
		int ai;
		cin>>ai;
		k+=(ai%2); //k表示每个家庭落单的人数
		r-=(ai/2); //r最终表示还剩下几排座位
		ans+=ai-ai%2;
	}
	r*=2; //还剩r个座位
	ans+=min(r-k,k);
	cout<<ans<<endl;
}
signed main(){
    int t;
	cin>>t;
	while(t--){
		solve();
	}
	return 0;
}

B. Kar Salesman

题意

共有 \(n\) 中型号的车，第 \(i\) 种型号的车有 \(a_i\) 辆，每次 \(\text{Karel}\) 可以推荐别人购买至多 \(x\) 辆车，且这些为 不同型号

问至少要推销给多少个人才能卖完这些车

思路

求出车数量的总和（设为 \(sum\) ），和 \(a_i\) 的最大值（设为 \(mx\)），最终答案为：\(\displaystyle \max(mx,\lceil \frac{sum}{x} \rceil)\)

C++ 代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
void solve(){
	int n,x;
	cin>>n>>x;
	int mx=0,sum=0;
	for(int i=0;i<n;i++){
		int ai;
		cin>>ai;
		mx=max(mx,ai);
		sum+=ai;
	}
	cout<<max(mx,(sum+x-1)/x)<<endl;
}
signed main(){
    int t;
	cin>>t;
	while(t--){
		solve();
	}
	return 0;
}

C. Gerrymandering

题意

一个 \(2*n\) 的网格图，每格代表一个居民（需要进行投票选举，可以投给 A 也可以投给 J），保证 \(2n \bmod 3 =0\)，将它分成 连通的 \(3\) 个一组，这一组 将投给 三个人投的更多的人，如 \(2\) 个 A \(1\) 个 J，则这一组投给 A

问：若按最优方案分组，最终投给 \(A\) 的组最多有多少

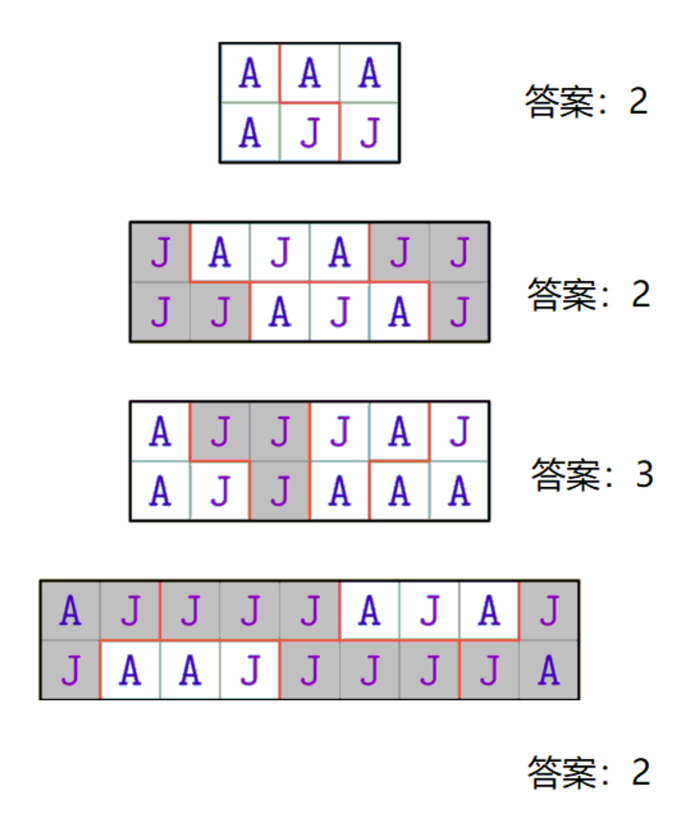
思路

需要动态规划，仅分为以下情况：

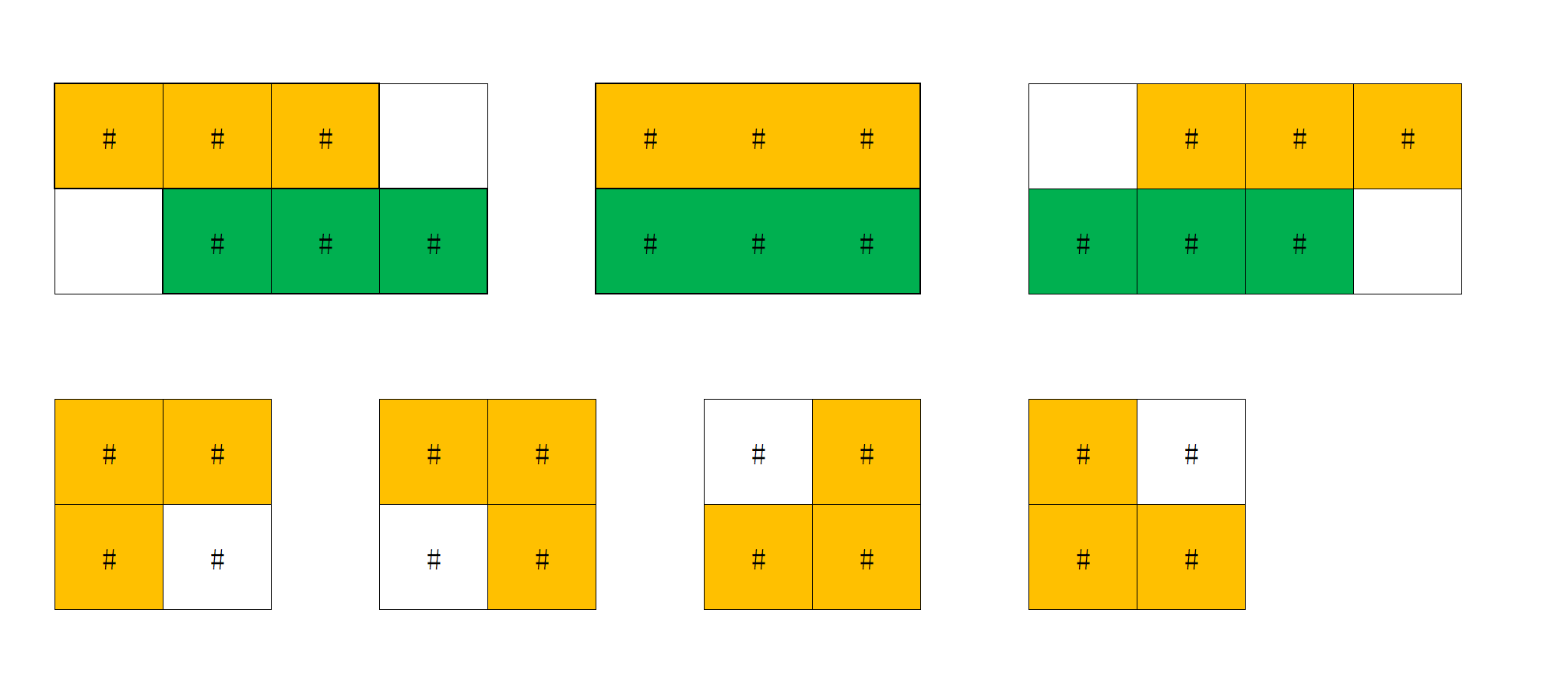
那么，只要转移正确就很简单

转移直接看代码

C++ 代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=2e9;
int n;
bool check(int a,int b,int c){
	int p=(a=='A'),q=(b=='A'),r=(c=='A');
	return (p+q+r>=2);
}
void solve(){
	cin>>n;
	string s[2];
	cin>>s[0]>>s[1];
	vector<vector<int> > dp(2,vector<int>(n+1,-inf));
	dp[0][0]=0;
	for(int i=0;i<n;i++){
		if(i%3==0){
			dp[0][i+3]=max(dp[0][i+3],
                           dp[0][i]+check(s[0][i],s[0][i+1],s[0][i+2])	//###
                           +check(s[1][i],s[1][i+1],s[1][i+2]));		//###

			dp[0][i+1]=max(dp[0][i+1],									//##
                           dp[0][i]+check(s[0][i],s[1][i],s[0][i+1]));	//#.

			dp[1][i+1]=max(dp[1][i+1],										//#.
                           dp[0][i]+check(s[0][i],s[1][i],s[1][i+1]));		//##

		}else if(i%3==1){
			if(i<n-3){
				dp[0][i+3]=max(dp[0][i+3],
                               dp[0][i]+check(s[0][i+1],s[0][i+2],s[0][i+3])	//.###
                               +check(s[1][i],s[1][i+1],s[1][i+2]));			//###.

				dp[1][i+3]=max(dp[1][i+3],
                               dp[1][i]+check(s[0][i],s[0][i+1],s[0][i+2])	//###.
                               +check(s[1][i+1],s[1][i+2],s[1][i+3]));		//.###
			}

			dp[0][i+2]=max(dp[0][i+2],										//.#
                           dp[0][i]+check(s[1][i],s[1][i+1],s[0][i+1]));	//##

			dp[0][i+2]=max(dp[0][i+2],										//##
                           dp[1][i]+check(s[0][i],s[0][i+1],s[1][i+1]));	//.#
		}
	}
	cout<<dp[0][n]<<endl;
}
signed main(){
    int t
	cin>>t;
	while(t--){
		solve();
	}
	return 0;
}

D1. Asesino (Easy Version)

题意

这是一道 交互题

有一种游戏，共有三种角色：Knight, Knave, Impostor，可以理解为：好人、坏人和内鬼

每局游戏有 \(n\) 个人，其中有 \(1\) 个内鬼，若干个好人和坏人（可能 \(0\) 个）

你忘记了每个人的角色，但是，你可以问玩家 \(i\) ：玩家 \(j\) 是不是好人？询问格式：? i j

玩家 \(i\) 会回答你 1 表示是好人，0 表示不是好人

以下为不同身份的回答表格：

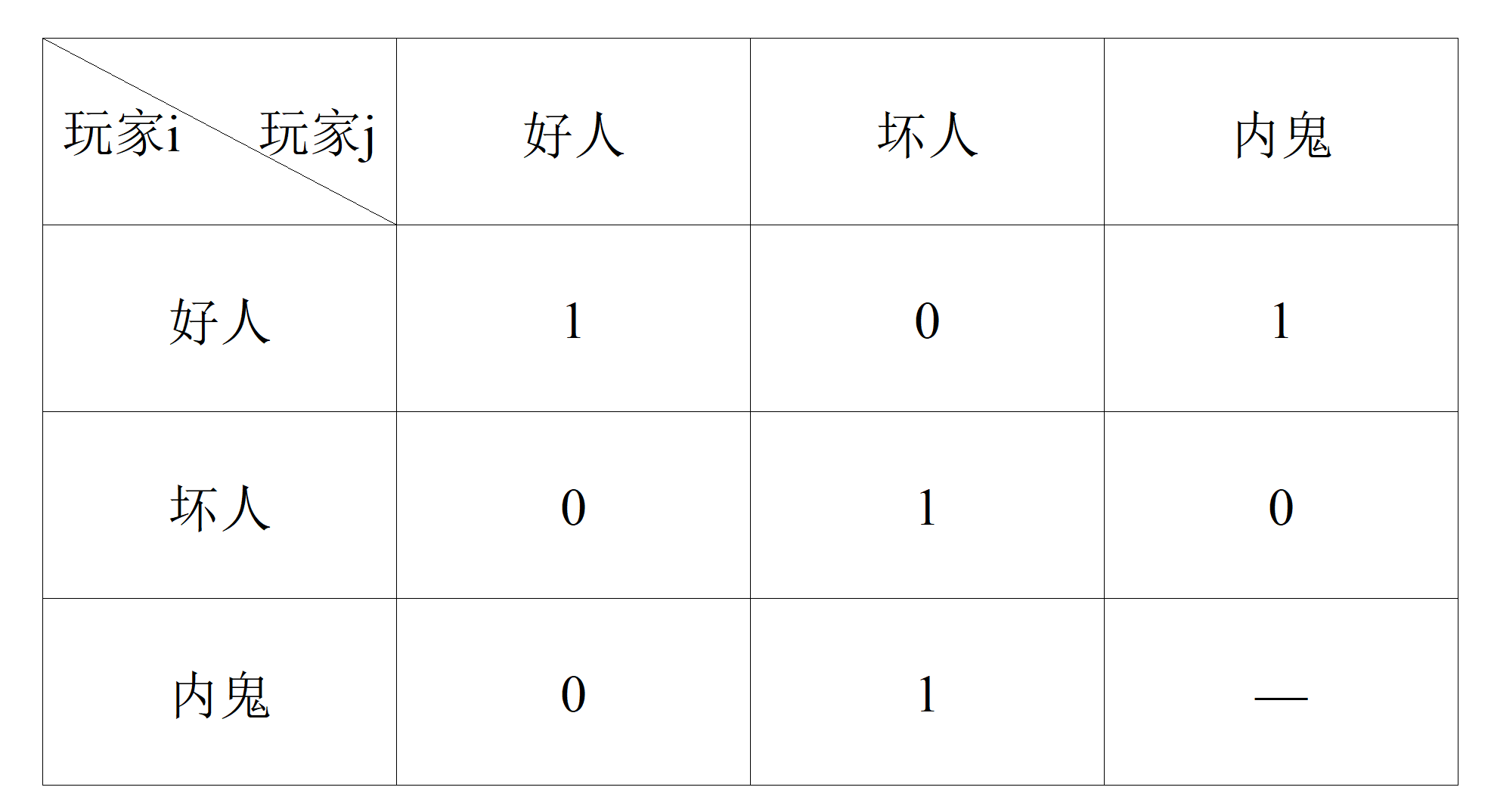
最多询问 \(n+69\) 次，请找出内鬼是玩家几，格式为 ! i

思路

观察表格发现，若 \([i\ 认为 \ j 的身份]\) 和 \([j \ 认为\ i\ 的身份]\) 不同，那么 \(i\) 和 \(j\) 中必定有一个内鬼

那么我们可以问每两个相邻的人，\(i\) 和 \(i+1\) 互相问，\(i+2\) 和 \(i+3\) 互相问，以此类推，最终找到 \(k\) 和 \(k+1\) 不同的位置，再和其他的比较，就可以得到内鬼的位置

C++ 代码

#include<bits/stdc++.h>
using namespace std;
int n;
bool query(int a,int b){
	cout<<"? "<<a<<" "<<b<<endl;
	int p;
	cin>>p;
	cout<<"? "<<b<<" "<<a<<endl;
	int q;
	cin>>q;
	return p!=q;
}
void solve(){
	cin>>n;
	int pos=-1;
	for(int i=1;i<n;i+=2){
		bool flag=query(i,i+1);
		if(flag){
			pos=i;
			break;
		}
	}
	if(pos==-1){
		cout<<"! "<<n<<endl;
	}else if(query(pos,pos>1?pos-1:pos+2)){
		cout<<"! "<<pos<<endl;
	}else{
		cout<<"! "<<pos+1<<endl;
	}
}
int main(){
    int t;
	cin>>t;
	while(t--){
		solve();
	}
	return 0;
}