最小生成树--克鲁斯卡尔算法（Kruskal）

按照惯例，接下来是本篇目录：

$1 什么是最小生成树？

$2 什么是克鲁斯卡尔算法？

$3 克鲁斯卡尔算法的例题

摘要：本片讲的是最小生成树中的玄学算法--克鲁斯卡尔算法，然后就没有然后了。

$1 什么是最小生成树？

•定义：

　　先引入一个定理：N个点用N-1条边连接成一个联通块，形成的图形只可能是树，没有别的可能；

　　根据这个定理，我们定义：在一个有N个点的图中，选出N-1条边出来，连接所有N个点，这N-1条边的边权之和最小的方案；

•最小生成树之prim算法：

　  由于本蒟蒻还不会这个算法，所以暂时将这个算法放在这里，讲讲思路，代码实在不会打QAQ

　　算法思路：

　　1. 从图中选取一个节点作为起始节点（也是树的根节点），标记为已达；初始化所有未达节点到树的距离为到根节点的距离；

　　2. 从剩余未达节点中选取到树距离最短的节点i，标记为已达；更新未达节点到树的距离（如果节点到节点i的距离小于现距离，则更新）；

　　3. 重复步骤2直到所有n个节点均为已达。

$2 什么是克鲁斯卡尔算法？

接下来是正题--克鲁斯卡尔算法

•算法思路：

　　（1）将所有边的边权从小到大依次排列，并且均标为未选；

　　（2）选择最小的未选边；

　　（3）如果该边与前面所选的边无法构成回路，则选中该边，并标为已选；如果该边与前面所选的边构成了回路，则不选该边，并标为已选；

　　（4）重复（2）（3），直到所有点之间都有边相连；

•举个栗子：

　　以下面这个图为例：

　　

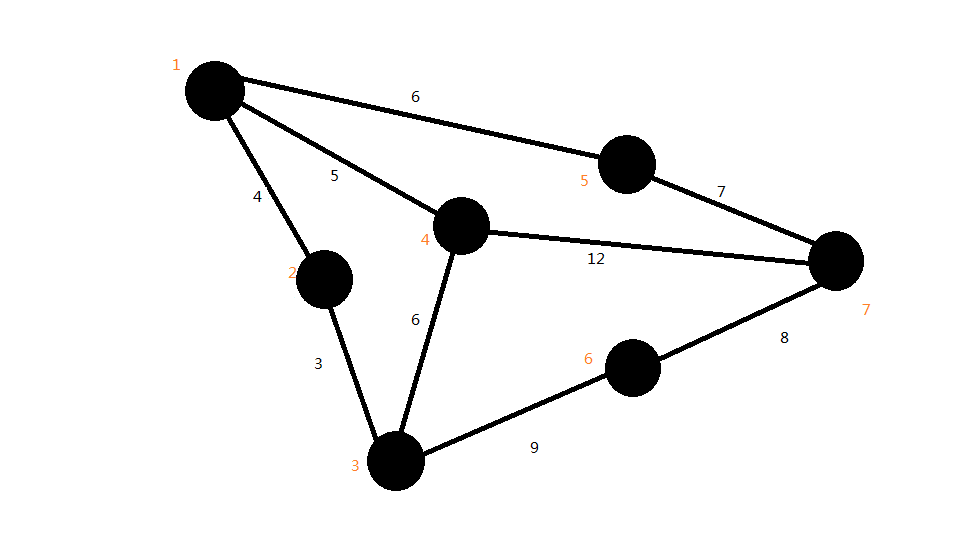
　　将各条边排序可得 3-4-5-6-6-7-8-9-12；

　　首先将最小的的边选上，即2--3，如图：

　　

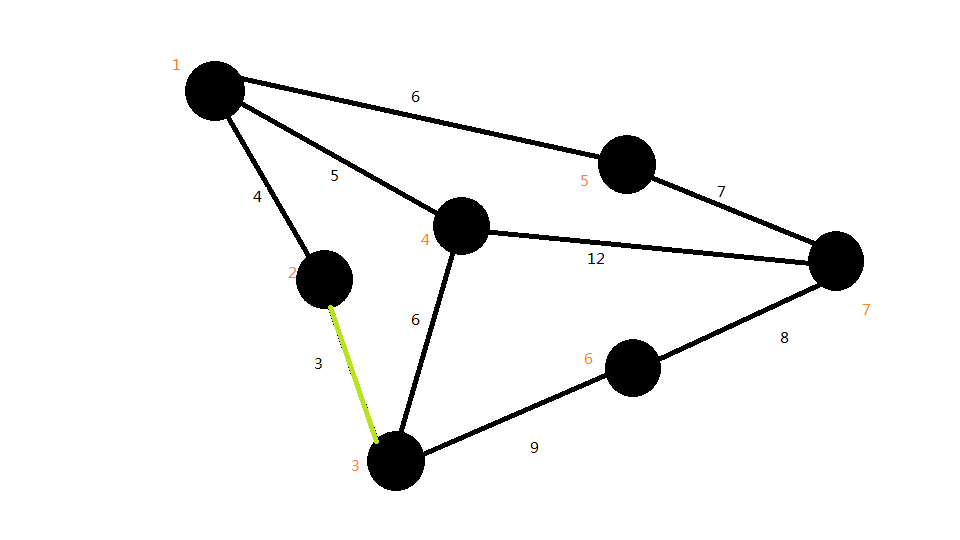
　　接下来，将第二条边选上，即1--2，如图：

　　

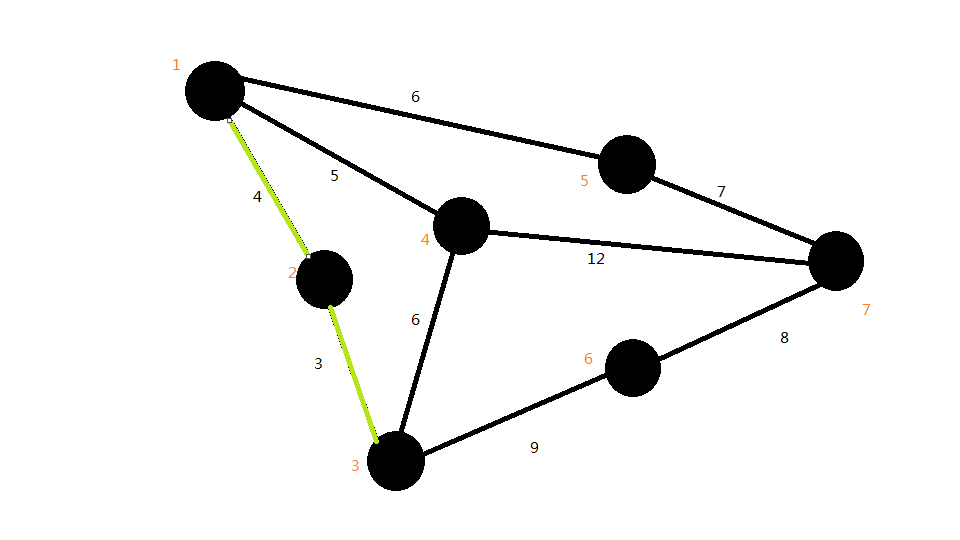
　　第三条边：

　　

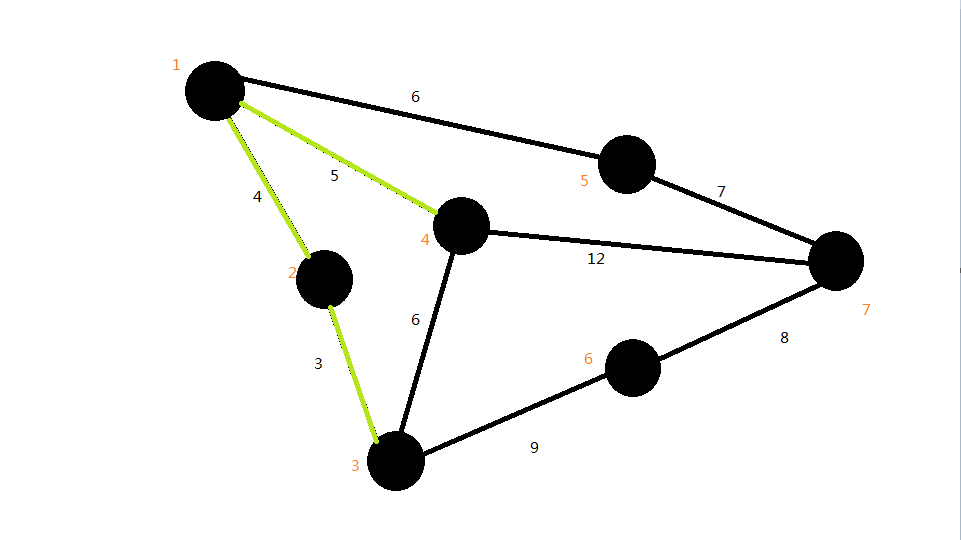
　　第四条边是6，但是与前三条边构成了回路，不选它；

　　第五条边：

　　

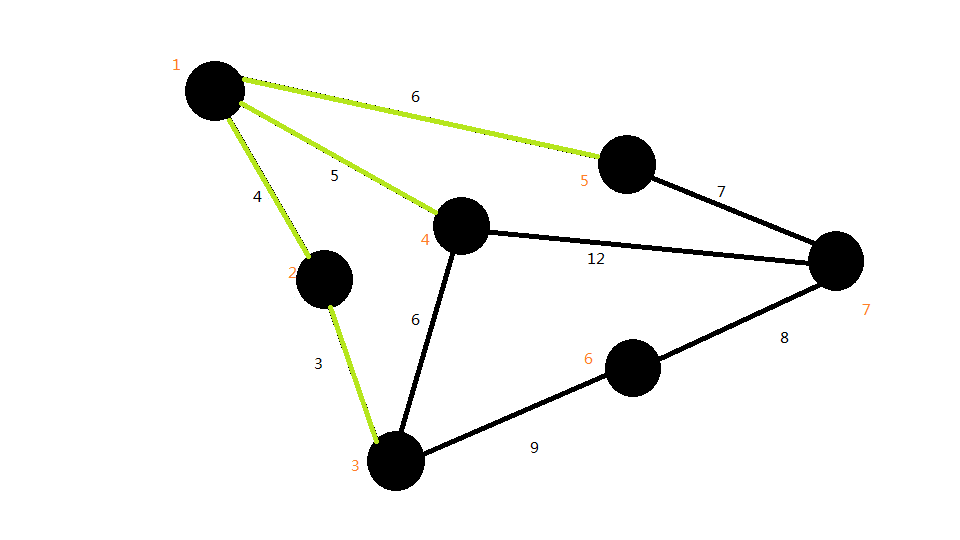
　　第六条边：

　　

　　最后一条边：

　　

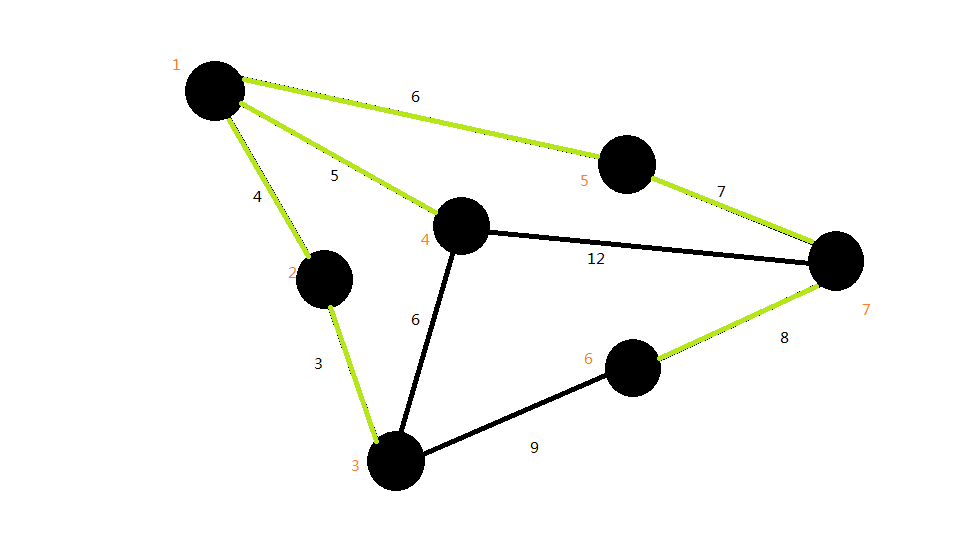
•代码实现：

　　

 struct point
 {
     int x;//始边
     int y;//终边
     int v;//边的权值
 };
 point a[];
 int fat[];
 int n,i,j,x,m,tot,k;
 int father(int x)//并查集中的查找
 {
     if(fat[x]!=x) fat[x]=father(fat[x]);
     return fat[x];
 }

 void unionn(int x,int y)//并查集中的合并
 {
     int fa=father(x);
     int fb=father(y);
     if(fa!=fb) fat[fa]=fb;
 }

 int cmp(const point &a,const point &b)
 {
     if(a.v<b.v) return ;//对边的权值进行排序
         else return ;
 }

 int main()
 {
     cin>>n;
     for(int i=;i<=n;++i)
         for(int j=;j<=n;++j)
         {
             cin>>x;
             if(x!=)
             {
                 m++;
                 a[m].x=i;a[m].y=j;a[m].v=x;
             }
         }
     for(int i=;i<=n;++i)  fat[i]=i;
     sort(a+,a+m+,cmp);
     for(int i=;i<=m;++i)
     {
         if(father(a[i].x)!=father(a[i].y))
         {
             unionn(a[i].x,a[i].y);
             tot+=a[i].v;
             k++;
         }//如果不能构成一个联通块，就将现在的这条边加入并查集
         if(k==n-) break;//否则将现在的这条边撇开不管
     }
     cout<<tot;
     return ;
 }

　　神仙们想必都已经看出来了，克鲁斯卡尔算法用到了并查集的思想（不会并查集的神仙戳这儿），还是很好理解的。

$3 克鲁斯卡尔算法的例题

•有且只有的一个例题： 洛谷P1546 最短网络 Agri-Net：

题目背景

农民约翰被选为他们镇的镇长！他其中一个竞选承诺就是在镇上建立起互联网，并连接到所有的农场。当然，他需要你的帮助。

题目描述

约翰已经给他的农场安排了一条高速的网络线路，他想把这条线路共享给其他农场。为了用最小的消费，他想铺设最短的光纤去连接所有的农场。

你将得到一份各农场之间连接费用的列表，你必须找出能连接所有农场并所用光纤最短的方案。每两个农场间的距离不会超过100000

输入输出格式

输入格式：

第一行： 农场的个数，N（3<=N<=100）。

第二行..结尾: 后来的行包含了一个N*N的矩阵,表示每个农场之间的距离。理论上，他们是N行，每行由N个用空格分隔的数组成，实际上，他们限制在80个字符，因此，某些行会紧接着另一些行。当然，对角线将会是0，因为不会有线路从第i个农场到它本身。

输出格式：

只有一个输出，其中包含连接到每个农场的光纤的最小长度。

输入输出样例

　　输入样例#1： 复制

　　4
　　0 4 9 21
　　4 0 8 17
　　9 8 0 16
　　21 17 16 0

　　输出样例#1： 复制

　　28
接下来是我懒得讲的代码（和上面一样）

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 struct point
 {
     int x;
     int y;
     int v;
 };
 point a[];
 int fat[];
 int n,i,j,x,m,tot,k;
 int father(int x)
 {
     if(fat[x]!=x) fat[x]=father(fat[x]);
     return fat[x];
 }

 void unionn(int x,int y)
 {
     int fa=father(x);
     int fb=father(y);
     if(fa!=fb) fat[fa]=fb;
 }

 int cmp(const point &a,const point &b)
 {
     if(a.v<b.v) return ;
         else return ;
 }

 int main()
 {
     cin>>n;
     for(int i=;i<=n;++i)
         for(int j=;j<=n;++j)
         {
             cin>>x;
             if(x!=)
             {
                 m++;
                 a[m].x=i;a[m].y=j;a[m].v=x;
             }
         }
     for(int i=;i<=n;++i)  fat[i]=i;
     sort(a+,a+m+,cmp);
     for(int i=;i<=m;++i)
     {
         if(father(a[i].x)!=father(a[i].y))
         {
             unionn(a[i].x,a[i].y);
             tot+=a[i].v;
             k++;
         }
         if(k==n-) break;
     }
     cout<<tot;
     return ;
 }

enddd~~