bzoj 2127 happiness【最小割+dinic】

参考：https://www.cnblogs.com/chenyushuo/p/5144957.html 不得不说这个建图方法真是非常妙啊

假设S点选理，T点选文，a[i][j]为(i,j)选文收益，b[i][j]为(i,j)选理收益，c[i][j]为同时选文收益，d[i][j]为同时选文收益。

那么对于每个点x=(i+1)*m+j，我们连接

\[c[s,x]=b[i][j]
\]

\[c[x,t]=a[i][j]
\]

对于有利益相关的x，y两点，连接

\[c[s,x]=d[i][j]/2
\]

\[c[s,y]=d[i][j]/2
\]

\[c[x,t]=c[i][j]/2
\]

\[c[y,t]=c[i][j]/2
\]

\[c[x,y]=c[i][j]/2+d[i][j]/2
\]

\[c[y,x]=c[i][j]/2+d[i][j]/2
\]

建完的图：



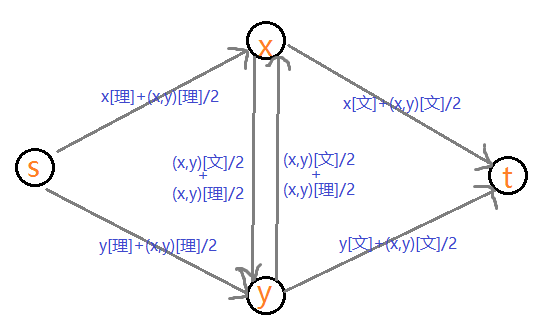
然后考虑最小割，下面枚举几种情况：

都选文，即割掉了x选理，y选理和(x,y)都选理：



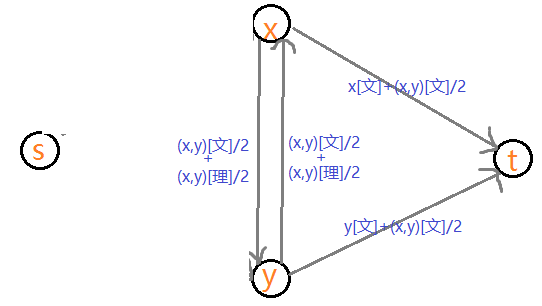
都选理，即割掉了x选文，y选文和(x,y)都选文：



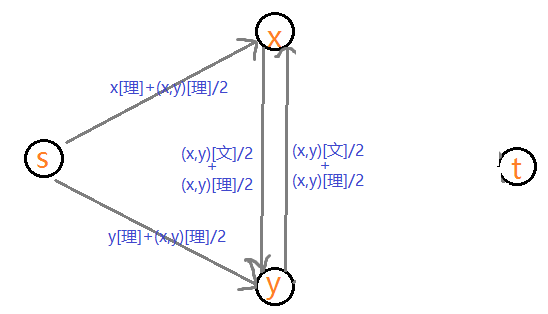
x选文y选理，即割掉了x选理，y选文，(x,y)都选理/+(x,y)都选理/2+(x,y)都选文/2+(x,y)都选文/2，即，割掉x选理，y选文，(x,y)都选理，(x,y)都选文：



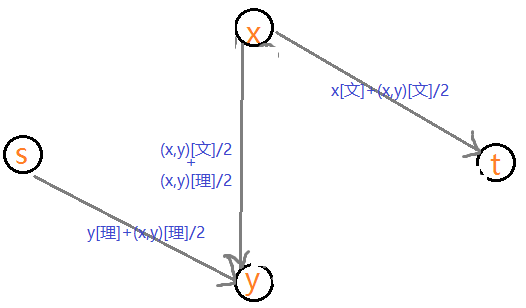
y选文x选理，即割掉了x选文，y选理，(x,y)都选理/+(x,y)都选理/2+(x,y)都选文/2+(x,y)都选文/2，即，割掉x选文，y选理，(x,y)都选理，(x,y)都选文：

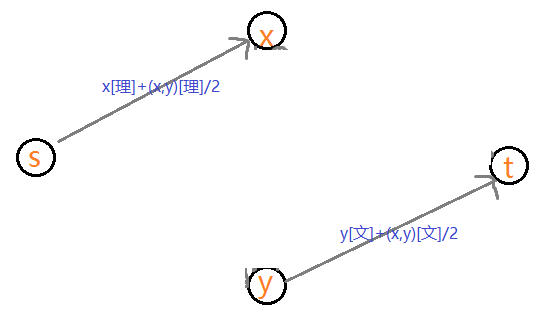
对于除以2的操作，为避免下取整的误差，我们选择把所有流量都*2，最后再/2。

$ ans=sum(全部收益）- 最小割 $

p.s.用邻接表建图的时候先把每个点选单科的边连上，再练同时选的收益，否则会重

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int N=105,E=1000005,inf=1e9,P=500005;
int n,m,a[N][N],b[N][N],c[N][N],d[N][N],s,t,sum,cnt=1,h[P],le[N*N];
struct qwe
{
	int ne,to,va;
}e[E];
int read()
{
	int r=0;
	char p=getchar();
	while(p<'0'||p>'9')
		p=getchar();
	while(p>='0'&&p<='9')
	{
		r=r*10+p-48;
		p=getchar();
	}
	return r;
}
void add(int u,int v,int w)
{
	cnt++;
	e[cnt].ne=h[u];
	e[cnt].to=v;
	e[cnt].va=w;
	h[u]=cnt;
}
bool bfs()
{
	queue<int>q;
    memset(le,0,sizeof(le));
	le[s]=1;
	q.push(s);
    while(!q.empty())
    {
        int u=q.front();//cout<<u<<"AAAAAAAAAAAA"<<endl;
		q.pop();
        for(int i=h[u];i;i=e[i].ne)
            if(e[i].va&&!le[e[i].to])
            {
                le[e[i].to]=le[u]+1;
                q.push(e[i].to);
            }
    }
	// for(int i=0;i<=5;i++)
		// cout<<le[i]<<" ";
    return le[t];
 }
int dfs(int u,int f)
{//cout<<u<<" "<<f<<endl;
    if(u==t)
	{
		//cout<<"!!";
		return f;
	}
    int used=0;
    for(int i=h[u];i;i=e[i].ne)
	{
		//cout<<u<<" "<<e[i].to<<"   "<<e[i].va<<endl;;
        if(e[i].va>0&&le[e[i].to]==le[u]+1)
        {//cout<<"OK"<<endl;
            int w=dfs(e[i].to,min(f-used,e[i].va));
            e[i].va-=w;
            e[i^1].va+=w;
            used+=w;
            if(used==f)
				return f;
        }
	}
    if(!used)
		le[u]=-1;
    return used;
}
int dinic()
{
	int ans=0;
	while(bfs())
		ans+=dfs(s,inf);//,cout<<ans<<endl;
	return ans;
}
int main()
{
	n=read(),m=read();
	s=0,t=n*m+1;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			a[i][j]=read(),sum+=a[i][j];
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			b[i][j]=read(),sum+=b[i][j];
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			int x=(i-1)*m+j;
			add(s,x,b[i][j]<<1);
			add(x,s,0);
			add(x,t,a[i][j]<<1);
			add(t,x,0);
		}
	for(int i=1;i<n;i++)
		for(int j=1;j<=m;j++)
			c[i][j]=read(),sum+=c[i][j];
	for(int i=1;i<n;i++)
		for(int j=1;j<=m;j++)
			d[i][j]=read(),sum+=d[i][j];
	for(int i=1;i<n;i++)
		for(int j=1;j<=m;j++)
		{
			int x=(i-1)*m+j,y=i*m+j;
			add(s,x,d[i][j]);
			add(x,s,0);
			add(s,y,d[i][j]);
			add(y,s,0);
			add(x,y,c[i][j]+d[i][j]);
			add(y,x,c[i][j]+d[i][j]);
			add(x,t,c[i][j]);
			add(t,x,0);
			add(y,t,c[i][j]);
			add(t,y,0);
		}
	for(int i=1;i<=n;i++)
		for(int j=1;j<m;j++)
			c[i][j]=read(),sum+=c[i][j];
	for(int i=1;i<=n;i++)
		for(int j=1;j<m;j++)
			d[i][j]=read(),sum+=d[i][j];
	for(int i=1;i<=n;i++)
		for(int j=1;j<m;j++)
		{
			int x=(i-1)*m+j,y=(i-1)*m+j+1;
			add(s,x,d[i][j]);
			add(x,s,0);
			add(s,y,d[i][j]);
			add(y,s,0);
			add(x,y,c[i][j]+d[i][j]);
			add(y,x,c[i][j]+d[i][j]);
			add(x,t,c[i][j]);
			add(t,x,0);
			add(y,t,c[i][j]);
			add(t,y,0);
		}
	printf("%d\n",sum-(dinic()>>1));
	return 0;
}