●POJ 3608 Bridge Across Islands

题链：

http://poj.org/problem?id=3608

题解：

计算几何，求两个凸包间的最小距离，旋转卡壳

两个凸包间的距离，无非下面三种情况：

---

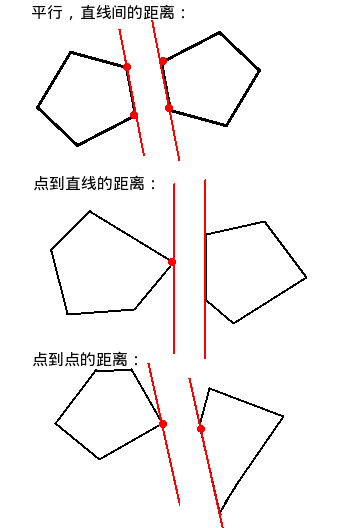
所以可以基于旋转卡壳的思想，去求最小距离。

（分别用i，j表示A，B凸包上枚举到的点，i的初始位置为A上y最小的顶点，j的初始位置为B上y最大的顶点。）

逆时针枚举凸包A的每一条边$\vec{A_iA_{i+1}}$，然后对另一个凸包B逆时针旋转卡壳，找到第一个$\vec{B_{j+1}B_j}\times\vec{A_iA_{i+1}}\geq0$

然后把$B_j与\vec{A_iA_{i+1}}$贡献答案，如果$\vec{B_{j+1}B_j}平行\vec{A_iA_{i+1}}$，则$B_j和B_{j+1}$都需要贡献答案。

代码：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 10050
using namespace std;
const double eps=1e-8;
int sign(double x){
	if(fabs(x)<=eps) return 0;
	return x<0?-1:1;
}
struct Point{
	double x,y;
	Point(double _x=0,double _y=0):x(_x),y(_y){}
	void Read(){scanf("%lf%lf",&x,&y);}
};
typedef Point Vector;
bool operator < (Point A,Point B){return sign(A.x-B.x)<0||(sign(A.x-B.x)==0&&sign(A.y-B.y)<0);}
Vector operator - (Point A,Point B){return Vector(A.x-B.x,A.y-B.y);}
double operator ^ (Vector A,Vector B){return A.x*B.y-A.y*B.x;}
double operator * (Vector A,Vector B){return A.x*B.x+A.y*B.y;}
Point D[MAXN],C1[MAXN],C2[MAXN];
int Andrew(int dnt,Point *C){
	int cnt=0,k;
	sort(D+1,D+dnt+1);
	for(int i=1;i<=dnt;i++){
		while(cnt>1&&sign((C[cnt]-C[cnt-1])^(D[i]-C[cnt-1]))<=0) cnt--;
		C[++cnt]=D[i];
	} k=cnt;
	for(int i=dnt-1;i>=1;i--){
		while(cnt>k&&sign((C[cnt]-C[cnt-1])^(D[i]-C[cnt-1]))<=0) cnt--;
		C[++cnt]=D[i];
	}
	return cnt-(dnt>1);
}
double GL(Vector A){//Get_Length
	return sqrt(A*A);
}
double TA(Point P,Point A,Point B){//Triangle_Area
	return fabs((P-A)^(P-B));
}
double DPS(Point P,Point A,Point B){//the_Distance_of_Point_to_Segment
	if(sign(GL(B-A))==0) return GL(P-A);
	if(sign((P-A)*(B-A))<0) return GL(P-A);
	if(sign((P-B)*(A-B))<0) return GL(P-B);
	return TA(P,A,B)/GL(B-A);
}
double RC(int ant,Point *A,int bnt,Point *B){//Rotating_Calipers
	A[ant+1]=A[1]; B[bnt+1]=B[1];
	int i=1,j=1,tmp; double d=1e300;
	for(int k=2;k<=ant;k++) if(sign(A[k].y-A[i].y)<0||(sign(A[k].y-A[i].y)==0&&sign(A[k].x-A[i].x)<0)) i=k;
	for(int k=2;k<=bnt;k++) if(sign(B[k].y-B[j].y)>0||(sign(B[k].y-B[j].y)==0&&sign(B[k].x-B[j].x)>0)) j=k;
	for(int ci=1;ci<=ant;ci++,i=i%ant+1){
		while((tmp=sign((A[i+1]-A[i])^(B[j]-B[j+1])))<0) j=j%bnt+1;
		d=min(d,DPS(B[j],A[i+1],A[i]));
		if(tmp==0) d=min(d,DPS(B[j+1],A[i+1],A[i]));
	}
	return d;
}
int main(){
	int n,m;
	while(~scanf("%d%d",&n,&m)&&(n||m)){
		for(int i=1;i<=n;i++) D[i].Read();
		n=Andrew(n,C1);
		for(int i=1;i<=m;i++) D[i].Read();
		m=Andrew(m,C2);
		printf("%.5lf\n",min(RC(n,C1,m,C2),RC(m,C2,n,C1)));
	}
	return 0;
}