PTA 深入虎穴 （正解）和树的同构

　　在上一篇博客中分享了尝试用单链表修改程序，虽然在Dev上运行没有错误，但是PTA设置的测试点有几个没有通过，具体不清楚问题出现在哪里，所以现在把之前正确的程序放在这里。

7-2 深入虎穴 (30 分)

 

著名的王牌间谍 007 需要执行一次任务，获取敌方的机密情报。已知情报藏在一个地下迷宫里，迷宫只有一个入口，里面有很多条通路，每条路通向一扇门。每一扇门背后或者是一个房间，或者又有很多条路，同样是每条路通向一扇门…… 他的手里有一张表格，是其他间谍帮他收集到的情报，他们记下了每扇门的编号，以及这扇门背后的每一条通路所到达的门的编号。007 发现不存在两条路通向同一扇门。

内线告诉他，情报就藏在迷宫的最深处。但是这个迷宫太大了，他需要你的帮助 —— 请编程帮他找出距离入口最远的那扇门。

输入格式：

输入首先在一行中给出正整数 N（<），是门的数量。最后 N 行，第 我行（1）按以下格式描述编号为 i 的那扇门背后能通向的门：

K D[1] D[2] ... D[K]

其中 K 是通道的数量，其后是每扇门的编号。

输出格式：

在一行中输出距离入口最远的那扇门的编号。题目保证这样的结果是唯一的。

输入样例：

13
3 2 3 4
2 5 6
1 7
1 8
1 9
0
2 11 10
1 13
0
0
1 12
0
0

输出样例：

12
根据题目要求和输入形式，分析数据存储结构，跟树结构相似，所以采用二叉树知识进行解题。
每行序号表示门序号，然后是这个门后面通向其他门个数，再来输入通向那些门。所以这个结构就像一个节点，然后它的孩子个数，跟树结构很像。

#include<iostream>
#include<queue>
using namespace std;

typedef struct //结构体数组，一个数据域存放门数量，另外用一个指针指向存放通道门序号的数组
{
    int doors;//门的数量
    int *p; //指向后面门的编号序列
}node;

int input(node *a,int n)//读入n扇门的信息 ，并返回跟所在门序号（下标）
{
    int i,j;
    bool *vi;
    vi=new bool[n+];//找出根结点的辅助数组

    for(i=;i<n+;i++)
        vi[i]=false;

    for(i=;i<n+;i++)
    {
        cin>>a[i].doors;
        if(a[i].doors)//门后面有通道
        {
            a[i].p=new int[a[i].doors];//申请存储门后面通道
            for(j=;j<a[i].doors;j++)
            {
                cin>>a[i].p[j];
                vi[a[i].p[j]]=true;
            }
        }
        else //door后面没有通向其他门的通道
        {
            a[i].p=NULL;
        } 

    }
    for(i=;i<n+;i++)//找出根结点所在下标（起点）
    {
        if(!vi[i]) return i;
    }
}

int level(node *a,int r)//从a[r]开始对a数组进行层次遍历，并返回遍历最后一个结点的序号
{//跟二叉树层次遍历相似，找到最远的门，也就是层次遍历最后的那个叶结点
    queue<int> q;
    int f,i;
    q.push(r);

    while(!q.empty())
    {
        f=q.front();
        q.pop();

        if(a[f].doors) //t号门后面有通道门
        {
            for(i=;i<a[f].doors;i++)
            {
                q.push(a[f].p[i]);
            }
        }
    }
    return f;//遍历到最后一个门序号，即是深度最大叶结点
}

int main()
{
    node *a;//用于存储整棵树
    int n,root;
    cin>>n;
    a=new node[n+];
    root=input(a,n);
//    cout<<root;
    cout<<level(a,root);
    return ;
}

7-1 树的同构 (30 分)

给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。

例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

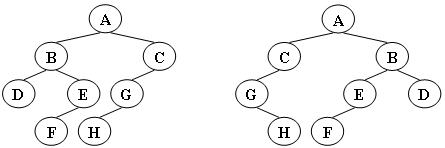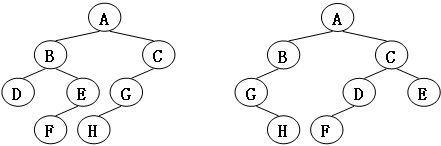图1                图2

现给定两棵树，请你判断它们是否是同构的。

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

这道题再次用到查找树的根结点的函数，跟之前完全一样，主要实现操作在于判断树同构的算法。
有以下几种情况：
1、两棵树为空，则同构
2、有一棵树为空，则不同构
3、都不为空，但是根结点名称不同，则不同构
4、都不为空，同构时的符合情况：
　　（1）左1=左2 且 右1=右2
　　（2）左1=右2 且 右1=左2
第4步判断操作可以基于前面3点，用递归方式实现。

#include<iostream>
#include<queue>
using namespace std;

typedef struct
{
    char name;
    int l,r;
} node;

int BuildTree(node T[]) //建立二叉树
{
    int i,N;
    bool check[]={false};//check数组用于查找树的根节点
    char x,y;
    cin>>N;

    if(N)//树结点个数不为0
    {
        for(i=;i<N;i++)
        {
            cin>>T[i].name>>x>>y; 

            if(x!='-')//若结点不为空，将节点索引放入左子树结点
            {
                T[i].l=x-'';
                check[T[i].l]=true;//记录此结点索引，在check数组将该位置置为true
            }
            else
            {
                T[i].l=-;//若结点为空，将其置为-1
            }

            if(y!='-')//同上，放入右子树
            {
                T[i].r=y-'';
                check[T[i].r]=true;
            }
            else
            {
                T[i].r=-;
            }
        }
        for(i=;i<N;i++)//遍历check数组，除了根结点之外，其它元素为true或-1
        {
            if(!check[i]) return i;//返回根结点下标
        }
    }
    else return -;// 若树为空，返回 -1

}

int treetonggou(node t1[],node t2[],int x,int y)//判断两棵树是否同构
{
    if(x==-&&y==-) return ;//两棵树为空，同构
    else if(x==-||y==-) return ;//有一棵树为空，不同构
    else if(t1[x].name!=t2[y].name) return ;//根结点名称不同，不同构
    else//递归判断所在根结点是否符合
    {
        return((treetonggou(t1,t2,t1[x].l,t2[y].l))&&(treetonggou(t1,t2,t1[x].r,t2[y].r))//判断两棵树此结点情况：左=左并且右=右
        ||(treetonggou(t1,t2,t1[x].l,t2[y].r))&&(treetonggou(t1,t2,t1[x].r,t2[y].l)));//左=右并且右=左
    }
}

int main()
{
    node t1[],t2[];
    int r1,r2;
    r1=BuildTree(t1);
    r2=BuildTree(t2);//cout<<r1<<" "<<r2;
    //cout<<treetonggou(t1,t2,r1,r2);
    if(treetonggou(t1,t2,r1,r2)) cout<<"Yes";
    else cout<<"No";
    return ;
}

做这道题开始不是很顺利，问题出在我用递归方式不对，在第4步时候是这样的：

int treetonggou(node t1[],node t2[],int x,int y)
{
    if(x==-&&y==-) return ;
    else if(x==-||y==-) return ;
    else if(t1[x].name!=t2[y].name) return ;
    else
    {
        if((treetonggou(t1,t2,t1[x].l,t2[y].l))&&(treetonggou(t1,t2,t1[x].r,t2[y].r))）
                return ；
        if((treetonggou(t1,t2,t1[x].l,t2[y].r))&&(treetonggou(t1,t2,t1[x].r,t2[y].l)));
                return ；
    }
}    

看是用了递归函数，之后一分析，其实没有用到前面基础进行递归，而是有自己的返回值了，没有用到递归的思想，在几个测试点没通过，因为没有考虑到各种情况，比如：

遍历结果相同，但树不同构；孩子结点相同，但根结点不同，树不同构。

之后几次修改，得到上面那个很长的return语句，最后通过。