#define INVSQRT2 0.707106781 平方根倒数速算法

转自 http://www.cnblogs.com/pkuoliver/archive/2010/10/06/1844725.html

源码下载地址：http://diducoder.com/sotry-about-sqrt.html

好吧，我承认我标题党了，不过既然你来了，就认真看下去吧，保证你有收获。

我们平时经常会有一些数据运算的操作，需要调用sqrt，exp，abs等函数，那么时候你有没有想过：这个些函数系统是如何实现的？就拿最常用的sqrt函数来说吧，系统怎么来实现这个经常调用的函数呢？

虽然有可能你平时没有想过这个问题，不过正所谓是“临阵磨枪，不快也光”，你“眉头一皱，计上心来”，这个不是太简单了嘛，用二分的方法，在一个区间中，每次拿中间数的平方来试验，如果大了，就再试左区间的中间数；如果小了，就再拿右区间的中间数来试。比如求sqrt(16)的结果，你先试（0+16）/2=8，8*8=64，64比16大，然后就向左移，试（0+8）/2=4，4*4=16刚好，你得到了正确的结果sqrt(16)=4。然后你三下五除二就把程序写出来了：

float SqrtByBisection(float n) //用二分法
{
	if(n<0) //小于0的按照你需要的处理
		return n;
	float mid,last;
	float low,up;
	low=0,up=n;
	mid=(low+up)/2;
	do
	{
		if(mid*mid>n)
			up=mid;
		else
			low=mid;
		last=mid;
		mid=(up+low)/2;
	}while(abs(mid-last) > eps);//精度控制
	return mid;
} 

然后看看和系统函数性能和精度的差别（其中时间单位不是秒也不是毫秒，而是CPU Tick，不管单位是什么，统一了就有可比性） 

从图中可以看出，二分法和系统的方法结果上完全相同，但是性能上整整差了几百倍。为什么会有这么大的区别呢？难道系统有什么更好的办法？难道。。。。哦，对了，回忆下我们曾经的高数课，曾经老师教过我们“牛顿迭代法快速寻找平方根”，或者这种方法可以帮助我们，具体步骤如下：

求出根号a的近似值：首先随便猜一个近似值x，然后不断令x等于x和a/x的平均数，迭代个六七次后x的值就已经相当精确了。 
例如，我想求根号2等于多少。假如我猜测的结果为4，虽然错的离谱，但你可以看到使用牛顿迭代法后这个值很快就趋近于根号2了： 
(       4  + 2/4        ) / 2 = 2.25 
(     2.25 + 2/2.25     ) / 2 = 1.56944.. 
( 1.56944..+ 2/1.56944..) / 2 = 1.42189.. 
( 1.42189..+ 2/1.42189..) / 2 = 1.41423.. 
....
这种算法的原理很简单，我们仅仅是不断用(x,f(x))的切线来逼近方程x^2-a=0的根。根号a实际上就是x^2-a=0的一个正实根，这个函数的导数是2x。也就是说，函数上任一点(x,f(x))处的切线斜率是2x。那么，x-f(x)/(2x)就是一个比x更接近的近似值。代入 f(x)=x^2-a得到x-(x^2-a)/(2x)，也就是(x+a/x)/2。

相关的代码如下：

float SqrtByNewton(float x)
{
	float val = x;//最终
	float last;//保存上一个计算的值
	do
	{
		last = val;
		val =(val + x/val) / 2;
	}while(abs(val-last) > eps);
	return val;
}

然后我们再来看下性能测试：

哇塞，性能提高了很多，可是和系统函数相比，还是有这么大差距，这是为什么呀？想啊想啊，想了很久仍然百思不得其解。突然有一天，我在网上看到一个神奇的方法，于是就有了今天的这篇文章，废话不多说，看代码先：

float InvSqrt(float x)
{
	float xhalf = 0.5f*x;
	int i = *(int*)&x; // get bits for floating VALUE
	i = 0x5f375a86- (i>>1); // gives initial guess y0
	x = *(float*)&i; // convert bits BACK to float
	x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
	x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
	x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy

	return 1/x;
}

然后我们最后一次来看下性能测试：

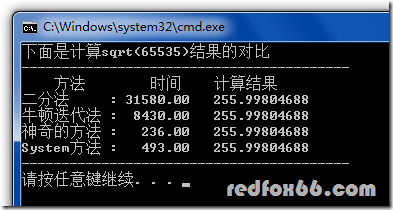这次真的是质变了，结果竟然比系统的还要好。。。哥真的是震惊了！！！哥吐血了！！！一个函数引发了血案！！！血案，血案。。。

到现在你是不是还不明白那个“鬼函数”，到底为什么速度那么快吗？不急，先看看下面的故事吧：

Quake-III Arena (雷神之锤3)是90年代的经典游戏之一。该系列的游戏不但画面和内容不错，而且即使计算机配置低，也能极其流畅地运行。这要归功于它3D引擎的开发者约翰-卡马克（John Carmack）。事实上早在90年代初DOS时代，只要能在PC上搞个小动画都能让人惊叹一番的时候，John Carmack就推出了石破天惊的Castle Wolfstein, 然后再接再励，doom, doomII, Quake...每次都把3-D技术推到极致。他的3D引擎代码资极度高效，几乎是在压榨PC机的每条运算指令。当初MS的Direct3D也得听取他的意见，修改了不少API。

最近，QUAKE的开发商ID SOFTWARE 遵守GPL协议，公开了QUAKE-III的原代码，让世人有幸目睹Carmack传奇的3D引擎的原码。这是QUAKE-III原代码的下载地址： 
http://www.fileshack.com/file.x?fid=7547

(下面是官方的下载网址，搜索 “quake3-1.32b-source.zip” 可以找到一大堆中文网页的。ftp://ftp.idsoftware.com/idstuff/source/quake3-1.32b-source.zip)

我们知道，越底层的函数，调用越频繁。3D引擎归根到底还是数学运算。那么找到最底层的数学运算函数（在game/code/q_math.c）， 必然是精心编写的。里面有很多有趣的函数，很多都令人惊奇，估计我们几年时间都学不完。在game/code/q_math.c里发现了这样一段代码。它的作用是将一个数开平方并取倒，经测试这段代码比(float)(1.0/sqrt(x))快4倍：

float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;

	x2 = number * 0.5F;
	y   = number;
	i   = * ( long * ) &y;   // evil floating point bit level hacking
	i   = 0x5f3759df - ( i >> 1 ); // what the fuck?
	y   = * ( float * ) &i;
	y   = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
	// y   = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed

	#ifndef Q3_VM
	#ifdef __linux__
		 assert( !isnan(y) ); // bk010122 - FPE?
	#endif
	#endif
	return y;
}  

函数返回1/sqrt(x)，这个函数在图像处理中比sqrt(x)更有用。 
注意到这个函数只用了一次叠代！（其实就是根本没用叠代，直接运算）。编译，实验，这个函数不仅工作的很好，而且比标准的sqrt()函数快4倍！要知道，编译器自带的函数，可是经过严格仔细的汇编优化的啊！ 
这个简洁的函数，最核心，也是最让人费解的，就是标注了“what the fuck?”的一句 
      i = 0x5f3759df - ( i >> 1 );

再加上y  = y * ( threehalfs - ( x2 * y * y ) ); 
两句话就完成了开方运算！而且注意到，核心那句是定点移位运算，速度极快！特别在很多没有乘法指令的RISC结构CPU上，这样做是极其高效的。

算法的原理其实不复杂,就是牛顿迭代法,用x-f(x)/f'(x)来不断的逼近f(x)=a的根。

没错，一般的求平方根都是这么循环迭代算的但是卡马克(quake3作者)真正牛B的地方是他选择了一个神秘的常数0x5f3759df 来计算那个猜测值，就是我们加注释的那一行，那一行算出的值非常接近1/sqrt(n)，这样我们只需要2次牛顿迭代就可以达到我们所需要的精度。好吧如果这个还不算NB,接着看:

普渡大学的数学家Chris Lomont看了以后觉得有趣，决定要研究一下卡马克弄出来的这个猜测值有什么奥秘。Lomont也是个牛人，在精心研究之后从理论上也推导出一个最佳猜测值，和卡马克的数字非常接近, 0x5f37642f。卡马克真牛，他是外星人吗？

传奇并没有在这里结束。Lomont计算出结果以后非常满意，于是拿自己计算出的起始值和卡马克的神秘数字做比赛，看看谁的数字能够更快更精确的求得平方根。结果是卡马克赢了... 谁也不知道卡马克是怎么找到这个数字的。

最后Lomont怒了，采用暴力方法一个数字一个数字试过来，终于找到一个比卡马克数字要好上那么一丁点的数字，虽然实际上这两个数字所产生的结果非常近似，这个暴力得出的数字是0x5f375a86。

Lomont为此写下一篇论文，"Fast Inverse Square Root"。 论文下载地址： 
http://www.math.purdue.edu/~clomont/Math/Papers/2003/InvSqrt.pdf 
http://www.matrix67.com/data/InvSqrt.pdf

参考：<IEEE Standard 754 for Binary Floating-Point Arithmetic><FAST INVERSE SQUARE ROOT>

最后，给出最精简的1/sqrt()函数：

float InvSqrt(float x)
{
	float xhalf = 0.5f*x;
	int i = *(int*)&x; // get bits for floating VALUE
	i = 0x5f375a86- (i>>1); // gives initial guess y0
	x = *(float*)&i; // convert bits BACK to float
	x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
	return x;
}  

大家可以尝试在PC机、51、AVR、430、ARM、上面编译并实验，惊讶一下它的工作效率。

前两天有一则新闻，大意是说 Ryszard Sommefeldt 很久以前看到这么样的一段 code (可能出自 Quake III 的 source code)：

float InvSqrt (float x)
{
	float xhalf = 0.5f*x;
	int i = *(int*)&x;
	i = 0x5f3759df - (i>>1);
	x = *(float*)&i;
	x = x*(1.5f - xhalf*x*x);
	return x;
}

他一看之下惊为天人，想要拜见这位前辈高人，但是一路追寻下去却一直找不到人；同时间也有其他人在找，虽然也没找到出处，但是 Chris Lomont 写了一篇论文 (in PDF) 解析这段 code 的算法 (用的是 Newton’s Method，牛顿法；比较重要的是后半段讲到怎么找出神奇的 0x5f3759df 的)。 
PS. 这个 function 之所以重要，是因为求 开根号倒数 这个动作在 3D 运算 (向量运算的部份) 里面常常会用到，如果你用最原始的 sqrt() 然后再倒数的话，速度比上面的这个版本大概慢了四倍吧… XD 
PS2. 在他们追寻的过程中，有人提到一份叫做 MIT HACKMEM 的文件，这是 1970 年代的 MIT 强者们做的一些笔记 (hack memo)，大部份是 algorithm，有些 code 是 PDP-10 asm 写的，另外有少数是 C code (有人整理了一份列表)

好了，故事就到这里结束了，希望大家能有有收获:)，我把源码也提供下载了，有兴趣的朋友们可以自己运行下试试看。

源码下载地址：http://diducoder.com/sotry-about-sqrt.html