MP和OMP算法
转载:有点无耻哈,全部复制别人的。写的不错
作者:scucj
文章链接:MP算法和OMP算法及其思想
主要介绍MP(Matching Pursuits)算法和OMP(Orthogonal Matching Pursuit)算法[1],这两个算法虽然在90年代初就提出来了,但作为经典的算法,国内文献(可能有我没有搜索到)都仅描述了算法步骤和简单的应用,并未对其进行详尽的分析,国外的文献还是分析的很透彻,所以我结合自己的理解,来分析一下写到博客里,算作笔记。
1. 信号的稀疏表示(sparse representation of signals)
给定一个过完备字典矩阵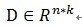 ,其中它的每列表示一种原型信号的原子。给定一个信号y,它可以被表示成这些原子的稀疏线性组合。信号 y 可以被表达为 y = Dx ,或者
,其中它的每列表示一种原型信号的原子。给定一个信号y,它可以被表示成这些原子的稀疏线性组合。信号 y 可以被表达为 y = Dx ,或者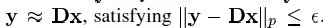 。 字典矩阵中所谓过完备性,指的是原子的个数远远大于信号y的长度(其长度很显然是n),即n<<k。
。 字典矩阵中所谓过完备性,指的是原子的个数远远大于信号y的长度(其长度很显然是n),即n<<k。
2.MP算法(匹配追踪算法)
2.1 算法描述
作为对信号进行稀疏分解的方法之一,将信号在完备字典库上进行分解。
假定被表示的信号为y,其长度为n。假定H表示Hilbert空间,在这个空间H里,由一组向量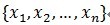 构成字典矩阵D,其中每个向量可以称为原子(atom),其长度与被表示信号 y 的长度n相同,而且这些向量已作为归一化处理,即|
构成字典矩阵D,其中每个向量可以称为原子(atom),其长度与被表示信号 y 的长度n相同,而且这些向量已作为归一化处理,即|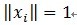 ,也就是单位向量长度为1。MP算法的基本思想:从字典矩阵D(也称为过完备原子库中),选择一个与信号 y 最匹配的原子(也就是某列),构建一个稀疏逼近,并求出信号残差,然后继续选择与信号残差最匹配的原子,反复迭代,信号y可以由这些原子来线性和,再加上最后的残差值来表示。很显然,如果残差值在可以忽略的范围内,则信号y就是这些原子的线性组合。如果选择与信号y最匹配的原子?如何构建稀疏逼近并求残差?如何进行迭代?我们来详细介绍使用MP进行信号分解的步骤:[1] 计算信号 y 与字典矩阵中每列(原子)的内积,选择绝对值最大的一个原子,它就是与信号 y 在本次迭代运算中最匹配的。用专业术语来描述:令信号
,也就是单位向量长度为1。MP算法的基本思想:从字典矩阵D(也称为过完备原子库中),选择一个与信号 y 最匹配的原子(也就是某列),构建一个稀疏逼近,并求出信号残差,然后继续选择与信号残差最匹配的原子,反复迭代,信号y可以由这些原子来线性和,再加上最后的残差值来表示。很显然,如果残差值在可以忽略的范围内,则信号y就是这些原子的线性组合。如果选择与信号y最匹配的原子?如何构建稀疏逼近并求残差?如何进行迭代?我们来详细介绍使用MP进行信号分解的步骤:[1] 计算信号 y 与字典矩阵中每列(原子)的内积,选择绝对值最大的一个原子,它就是与信号 y 在本次迭代运算中最匹配的。用专业术语来描述:令信号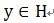 ,从字典矩阵中选择一个最为匹配的原子,满足
,从字典矩阵中选择一个最为匹配的原子,满足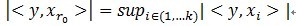 ,r0 表示一个字典矩阵的列索引。这样,信号 y 就被分解为在最匹配原子
,r0 表示一个字典矩阵的列索引。这样,信号 y 就被分解为在最匹配原子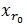 的垂直投影分量和残值两部分,即:
的垂直投影分量和残值两部分,即: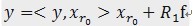 。[2]对残值R1f进行步骤[1]同样的分解,那么第K步可以得到:
。[2]对残值R1f进行步骤[1]同样的分解,那么第K步可以得到:
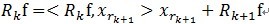 , 其中
, 其中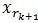 满足
满足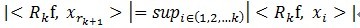 。可见,经过K步分解后,信号 y 被分解为:
。可见,经过K步分解后,信号 y 被分解为: ,其中
,其中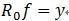 。
。
2.2 继续讨论
(1)为什么要假定在Hilbert空间中?Hilbert空间就是定义了完备的内积空。很显然,MP中的计算使用向量的内积运算,所以在在Hilbert空间中进行信号分解理所当然了。什么是完备的内积空间?篇幅有限就请自己搜索一下吧。
(2)为什么原子要事先被归一化处理了,即上面的描述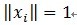 。内积常用于计算一个矢量在一个方向上的投影长度,这时方向的矢量必须是单位矢量。MP中选择最匹配的原子是,是选择内积最大的一个,也就是信号(或是残值)在原子(单位的)垂直投影长度最长的一个,比如第一次分解过程中,投影长度就是
。内积常用于计算一个矢量在一个方向上的投影长度,这时方向的矢量必须是单位矢量。MP中选择最匹配的原子是,是选择内积最大的一个,也就是信号(或是残值)在原子(单位的)垂直投影长度最长的一个,比如第一次分解过程中,投影长度就是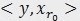 。
。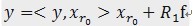 ,三个向量,构成一个三角形,且
,三个向量,构成一个三角形,且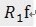 和
和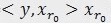 正交(不能说垂直,但是可以想象二维空间这两个矢量是垂直的)。
正交(不能说垂直,但是可以想象二维空间这两个矢量是垂直的)。
(3)MP算法是收敛的,因为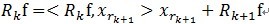 ,
,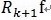 和
和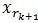 正交,由这两个可以得出
正交,由这两个可以得出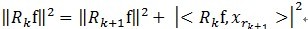 ,得出每一个残值比上一次的小,故而收敛。
,得出每一个残值比上一次的小,故而收敛。
2.3 MP算法的缺点
如上所述,如果信号(残值)在已选择的原子进行垂直投影是非正交性的,这会使得每次迭代的结果并不少最优的而是次最优的,收敛需要很多次迭代。举个例子说明一下:在二维空间上,有一个信号 y 被 D=[x1, x2]来表达,MP算法迭代会发现总是在x1和x2上反复迭代,即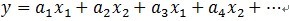 ,这个就是信号(残值)在已选择的原子进行垂直投影的非正交性导致的。再用严谨的方式描述[1]可能容易理解:在Hilbert空间H中,
,这个就是信号(残值)在已选择的原子进行垂直投影的非正交性导致的。再用严谨的方式描述[1]可能容易理解:在Hilbert空间H中,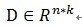 ,
,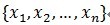 ,定义
,定义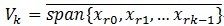 ,就是它是这些向量的张成中的一个,MP构造一种表达形式:
,就是它是这些向量的张成中的一个,MP构造一种表达形式: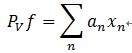 ;这里的Pvf表示 f在V上的一个正交投影操作,那么MP算法的第 k 次迭代的结果可以表示如下(前面描述时信号为y,这里变成f了,请注意):
;这里的Pvf表示 f在V上的一个正交投影操作,那么MP算法的第 k 次迭代的结果可以表示如下(前面描述时信号为y,这里变成f了,请注意):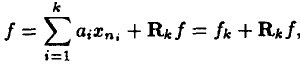
如果  是最优的k项近似值,当且仅当
是最优的k项近似值,当且仅当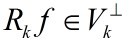 。由于MP仅能保证
。由于MP仅能保证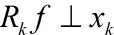 ,所以
,所以 一般情况下是次优的。这是什么意思呢?
一般情况下是次优的。这是什么意思呢? 是k个项的线性表示,这个组合的值作为近似值,只有在第k个残差和
是k个项的线性表示,这个组合的值作为近似值,只有在第k个残差和 正交,才是最优的。如果第k个残值与
正交,才是最优的。如果第k个残值与 正交,意味这个残值与fk的任意一项都线性无关,那么第k个残值在后面的分解过程中,不可能出现fk中已经出现的项,这才是最优的。而一般情况下,不能满足这个条件,MP一般只能满足第k个残差和xk正交,这也就是前面为什么提到“信号(残值)在已选择的原子进行垂直投影是非正交性的”的原因。如果第k个残差和fk不正交,那么后面的迭代还会出现fk中已经出现的项,很显然fk就不是最优的,这也就是为什么说MP收敛就需要更多次迭代的原因。不是说MP一定得到不到最优解,而且其前面描述的特性导致一般得到不到最优解而是次优解。那么,有没有办法让第k个残差与
正交,意味这个残值与fk的任意一项都线性无关,那么第k个残值在后面的分解过程中,不可能出现fk中已经出现的项,这才是最优的。而一般情况下,不能满足这个条件,MP一般只能满足第k个残差和xk正交,这也就是前面为什么提到“信号(残值)在已选择的原子进行垂直投影是非正交性的”的原因。如果第k个残差和fk不正交,那么后面的迭代还会出现fk中已经出现的项,很显然fk就不是最优的,这也就是为什么说MP收敛就需要更多次迭代的原因。不是说MP一定得到不到最优解,而且其前面描述的特性导致一般得到不到最优解而是次优解。那么,有没有办法让第k个残差与 正交,方法是有的,这就是下面要谈到的OMP算法。
正交,方法是有的,这就是下面要谈到的OMP算法。
3.OMP算法
3.1 算法描述
OMP算法的改进之处在于:在分解的每一步对所选择的全部原子进行正交化处理,这使得在精度要求相同的情况下,OMP算法的收敛速度更快。
那么在每一步中如何对所选择的全部原子进行正交化处理呢?在正式描述OMP算法前,先看一点基础思想。
先看一个 k 阶模型,表示信号 f 经过 k 步分解后的情况,似乎很眼熟,但要注意它与MP算法不同之处,它的残值与前面每个分量正交,这就是为什么这个算法多了一个正交的原因,MP中仅与最近选出的的那一项正交。
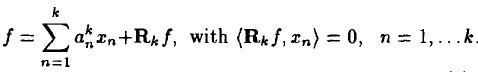 (1)
(1)
k + 1 阶模型如下:
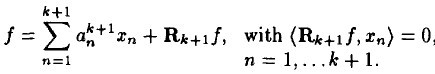 (2)
(2)
应用 k + 1阶模型减去k 阶模型,得到如下:
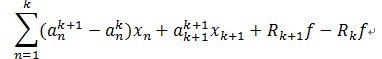 (3)
(3)
我们知道,字典矩阵D的原子是非正交的,引入一个辅助模型,它是表示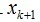 对前k个项
对前k个项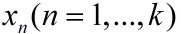 的依赖,描述如下:
的依赖,描述如下:
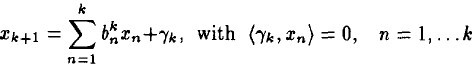 (4)
(4)
和前面描述类似,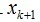 在span(x1, ...xk)之一上的正交投影操作,后面的项是残值。这个关系用数学符号描述:
在span(x1, ...xk)之一上的正交投影操作,后面的项是残值。这个关系用数学符号描述: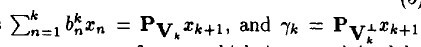
请注意,这里的 a 和 b 的上标表示第 k 步时的取值。
将(4)带入(3)中,有:
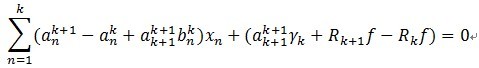 (5)
(5)
如果以下两个式子成立,(5)必然成立。
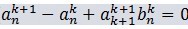 (6)
(6)
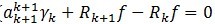 (7)
(7)
令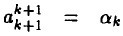 ,有
,有
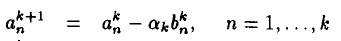
其中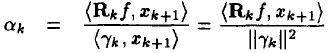 。
。
ak的值是由求法很简单,通过对(7)左右两边添加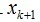 作内积消减得到:
作内积消减得到:
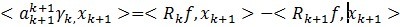
后边的第二项因为它们正交,所以为0,所以可以得出ak的第一部分。对于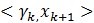 ,在(4)左右两边中与
,在(4)左右两边中与 作内积,可以得到ak的第二部分。
作内积,可以得到ak的第二部分。
对于(4),可以求出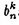 ,求的步骤请参见参考文件的计算细节部分。为什么这里不提,因为后面会介绍更简单的方法来计算。
,求的步骤请参见参考文件的计算细节部分。为什么这里不提,因为后面会介绍更简单的方法来计算。
3.2 收敛性证明
通过(7)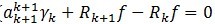 ,由于
,由于 与
与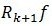 正交,将两个残值移到右边后求二范的平方,并将ak的值代入可以得到:
正交,将两个残值移到右边后求二范的平方,并将ak的值代入可以得到:
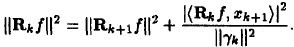
可见每一次残差比上一次残差小,可见是收敛的。
3.3 算法步骤
整个OMP算法的步骤如下:

由于有了上面的来龙去脉,这个算法就相当好理解了。
到这里还不算完,后来OMP的迭代运算用另外一种方法可以计算得知,有位同学的论文[2]描述就非常好,我就直接引用进来:


对比中英文描述,本质都是一样,只是有细微的差别。这里顺便贴出网一哥们写的OMP算法的代码,源出处不得而知,共享给大家。

再贴另外一个洋牛paper[3]中关于OMP的描述,之所以引入,是因为它描述的非常严谨,但是也有点苦涩难懂,不过有了上面的基础,就容易多了。

它的描述中的Sweep步骤就是寻找与当前残差最大的内积时列在字典矩阵D中的索引,它的这个步骤描述说明为什么要选择内积最大的以及如何选择。见下图,说的非常清晰。
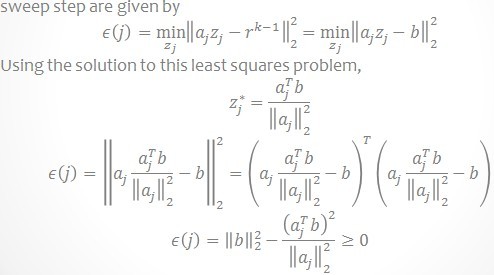
它的算法步骤Update Provisional Solution中求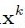 很简单,就是在 b = Ax 已知 A和b求x, 在x的最小二范就是A的伪逆与b相乘,即:
很简单,就是在 b = Ax 已知 A和b求x, 在x的最小二范就是A的伪逆与b相乘,即:
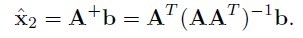
看上去头疼,其实用matlab非常简单,看看上面的matlab的代码就明白了。
我们可以看得出来,算法流程清晰明了,还是很好理解的。这正是OMP算法的魅力,作为工具使用简单,背后却隐藏着很有趣的思想。
写这篇博客的目的,是因为搜索了一下,MP和OMP没有人很详细的介绍。文献[1]讲的很清楚的,大家有兴趣可以找来看看。不要被老板发现我居然在搜中文文献还写中文博客。
MP和OMP算法的更多相关文章
- 稀疏分解中的MP与OMP算法
MP:matching pursuit匹配追踪 OMP:正交匹配追踪 主要介绍MP与OMP算法的思想与流程,解释为什么需要引入正交? !!今天发现一个重大问题,是在读了博主的正交匹配追踪(OMP)在稀 ...
- MP 及OMP算法解析
转载自http://blog.csdn.net/pi9nc/article/details/18655239 1,MP算法[盗用2] MP算法是一种贪心算法(greedy),每次迭代选取与当前样本残差 ...
- MP算法和OMP算法及其思想
主要介绍MP(Matching Pursuits)算法和OMP(Orthogonal Matching Pursuit)算法[1],这两个算法尽管在90年代初就提出来了,但作为经典的算法,国内文献(可 ...
- MP算法、OMP算法及其在人脸识别的应用
主要内容: 1.MP算法 2.OMP算法 3.OMP算法的matlab实现 4.OMP在压缩感知和人脸识别的应用 一.MP(Matching Pursuits)与OMP(Orthogonal Matc ...
- 浅谈压缩感知(十九):MP、OMP与施密特正交化
关于MP.OMP的相关算法与收敛证明,可以参考:http://www.cnblogs.com/AndyJee/p/5047174.html,这里仅简单陈述算法流程及二者的不同之处. 主要内容: MP的 ...
- OMP算法代码学习
正交匹配追踪(OMP)算法的MATLAB函数代码并给出单次测试例程代码 测量数M与重构成功概率关系曲线绘制例程代码 信号稀疏度K与重构成功概率关系曲线绘制例程代码 参考来源:http://blog ...
- 压缩感知重构算法之OMP算法python实现
压缩感知重构算法之OMP算法python实现 压缩感知重构算法之CoSaMP算法python实现 压缩感知重构算法之SP算法python实现 压缩感知重构算法之IHT算法python实现 压缩感知重构 ...
- 压缩感知“Hello World”代码初步学习
压缩感知代码初学 实现:1-D信号压缩传感的实现 算法:正交匹配追踪法OMP(Orthogonal Matching Pursuit) >几个初学问题 1. 原始信号f是什么?我采集的是 ...
- 浅谈压缩感知(九):正交匹配追踪算法OMP
主要内容: OMP算法介绍 OMP的MATLAB实现 OMP中的数学知识 一.OMP算法介绍 来源:http://blog.csdn.net/scucj/article/details/7467955 ...
随机推荐
- MVC输出缓存(OutputCache参数详解)
版权声明:本文为博主原创文章,未经博主允许转载随意. https://blog.csdn.net/kebi007/article/details/59199115 1.学习之前你应该知道这些 几乎每个 ...
- Excel 表格查找重复数据,去重复统计
找出表格是否有重复数据: =IF(AND(G20=G19,D20=D19),"是","否") 筛选移除[重复的数据]然后开始统计 =SUBTOTAL(9,E2: ...
- C# HttpWebResponse WebClient 基础连接已经关闭: 发送时发生错误.
https://blog.csdn.net/sun49842566/article/details/82802297 net 4.0 设置: ServicePointManager.SecurityP ...
- spring boot2+jpa+thymeleaf增删改查例子
参考这遍文章做了一个例子,稍微不同之处,原文是spring boot.mysql,这里改成了spring boot 2.Oracle. 一.pom.xml引入相关模块web.jpa.thymeleaf ...
- 伪分布式安装core-site.xml和hdfs-site.xml配置文件
hadoop的伪分布式安装流程如下所示: 其中core-site.xml和hdfs-site.xml是两个很重要的配置文件. core-site.xml <configuration> & ...
- ubuntu18.04中python虚拟环境的安装
一:下载虚拟环境安装包 sudo apt install virtualenv sudo apt install virtualenvwrapper pwd 查看当前目录 ls -all 查看是否有 ...
- 在input中输入需要的数据,使用qrcode,点击生成二维码
话不多说直接上代码 <!DOCTYPE html> <html> <head> <meta http-equiv="Content-Type&quo ...
- CentOs系统设置python版本
一.针对当前终端生效 最近云服务器安装了centos7系统,python默认版本是2.7.5,但是习惯用anaconda3, 安装anaconda3之后将系统默认python版本更改为python3. ...
- gii的使用
假设有表link 在backend中生成子模块content 生成子模块模型common/models/Link 生成模块content中的crud 配置别名 在backend/config/main ...
- 基于Python——实现远程下载sftp文件(只下载.zip文件)
[背景]远程下载发布包等文件时,总是要使用WinSCP等工具登陆拖动.今天就介绍一种使用python下载文件到本地的方法. [代码实现] import paramiko # paramiko模块,基于 ...
