机器学习--Logistic回归

logistic回归

很多时候我们需要基于一些样本数据去预测某个事件是否发生，如预测某事件成功与失败，某人当选总统是否成功等。

这个时候我们希望得到的结果是 bool型的,即 true or false

我们最先想到的是通过最小二乘法求出线性回归模型，

即 Y = W^TX  = w₀x₀ +  w₁x₁ +  w₂x₂ + ...  +  w_nx_n 

X表示自变量向量，可以通过随机梯度算法求出上述的系数向量W

此时Y表示线性回归的预测值。

这时存在的问题是：

Y表示的是预测值，但是其可正，可负，可以很大，可以很小，我们无法通过Y得出二进制的结果

为了解决上面的问题，我们可以大胆假设该事件发生的概率的p且 logit(p) = Y

logit(p) 是一个统计学上的模型

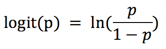
由logit (p ) = Y求得

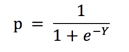
画图如下:

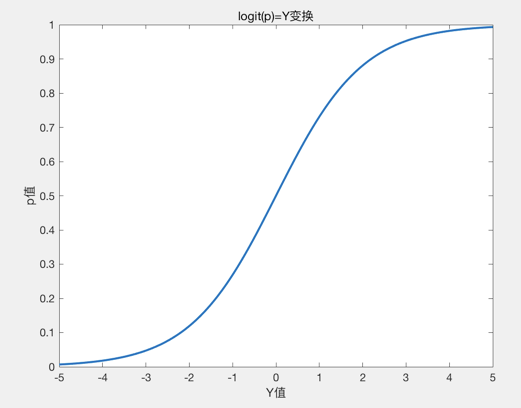
我们可以看出，对于任意的Y值，假设的概率值p都分布在[0，1]之间

这样我们可以规定任何p大于0.5的数据被分入1类，小于0.5被归入0类，从而得到bool型的结果

事实证明，上述的logit(p) 模型，在处理这种二分类预测中非常有用

这便是logistic回归

用logistic回归预测实例

数据集来源:  http://archive.ics.uci.edu/ml/datasets/Haberman%27s+Survival

数据集说明：

该数据集包含了1958年-1970年在芝加哥大学的比林斯医院接受过乳房癌症手术的病人的存活率。数据集样例如下：

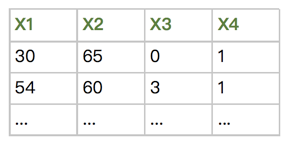
X1: 手术时病人年龄
X2: 患者手术年(年- 1900年)
X3: 检测阳性腋窝淋巴结数目(数值)
X4: 生存状态(class属性)1--患者活了5年或更长 , 0---病人在5年内死亡。

求当一个病人的数据为[X1,X2,X3] = [34,66,9]时我们可以通过logistic回归预测病人手术后是否有可能活过5年？

代码

 # -*- coding:utf-8 -*-
 import numpy as np

 def load_data(file_name):
     # 载入数据
     data_mat = []
     labels = []

     with open(file_name) as file:
         for line in file.readlines():
             line_arr = line.strip().split(',')
             data_mat.append([float(line_arr[0]), float(line_arr[1]), float(line_arr[2])])
             labels.append(int(line_arr[3]))
     return data_mat, labels

 def sigmoid(x):
     # 阶跃函数
     if -x > np.log(np.finfo(type(x)).max):
         return 0.0
     else:
         return 1.0 / (1 + np.exp(-x))

 def grad_ascent(data_mat, data_labels, num_iter=200):
     """随机梯度上升算法"""
     data_mat = np.array(data_mat)
     m, n = np.shape(data_mat)

     weights = np.ones(n).astype(np.float)
     for j in range(num_iter):
         data_index = list(range(m))
         for i in range(m):
             alpha = 0.001 + 4 / (1.0 + j + i)

             random_index = int(np.random.uniform(0, len(data_index)))
             h = sigmoid(sum(data_mat[random_index] * weights))
             error = data_labels[random_index] - h
             weights = weights + alpha * error * data_mat[random_index]
             del (data_index[random_index])

     return weights

 def test(x, name):
     file_name = name
     data_mat, labels = load_data(file_name)
     weights = grad_ascent(data_mat, labels)
     print(weights)
     res = classify_vector(x, weights)
     print(res)

 def classify_vector(inx, weights):
     prob = sigmoid(sum(inx * weights))
     if prob > 0.5:
         return 1.0
     else:
         return 0.0

 name = 'data/haberman.txt'
 test([72, 63, 0], name)

执行结果为 0

说明改病人很可能术后活不过5年。

以上只是logistic 回归的一个简单测试，所有代码已上传 https://github.com/beiyan1911/machine_learning/tree/master/logistic_reg