2018 ECNA Regional Contest J. Watch Where You Step

题目链接：Watch Where You Step

题意

给定有向图的邻接矩阵，现在需要给该图增加边，使得如果两点可达必直接可达，求需要加边的数量。

题解

首先，如果给定 \(n\) 个结点的图中任意两点均可达，那么需要增加的边数为有向完全图的边数 $n * (n - 1) - $ 原来有的边数。

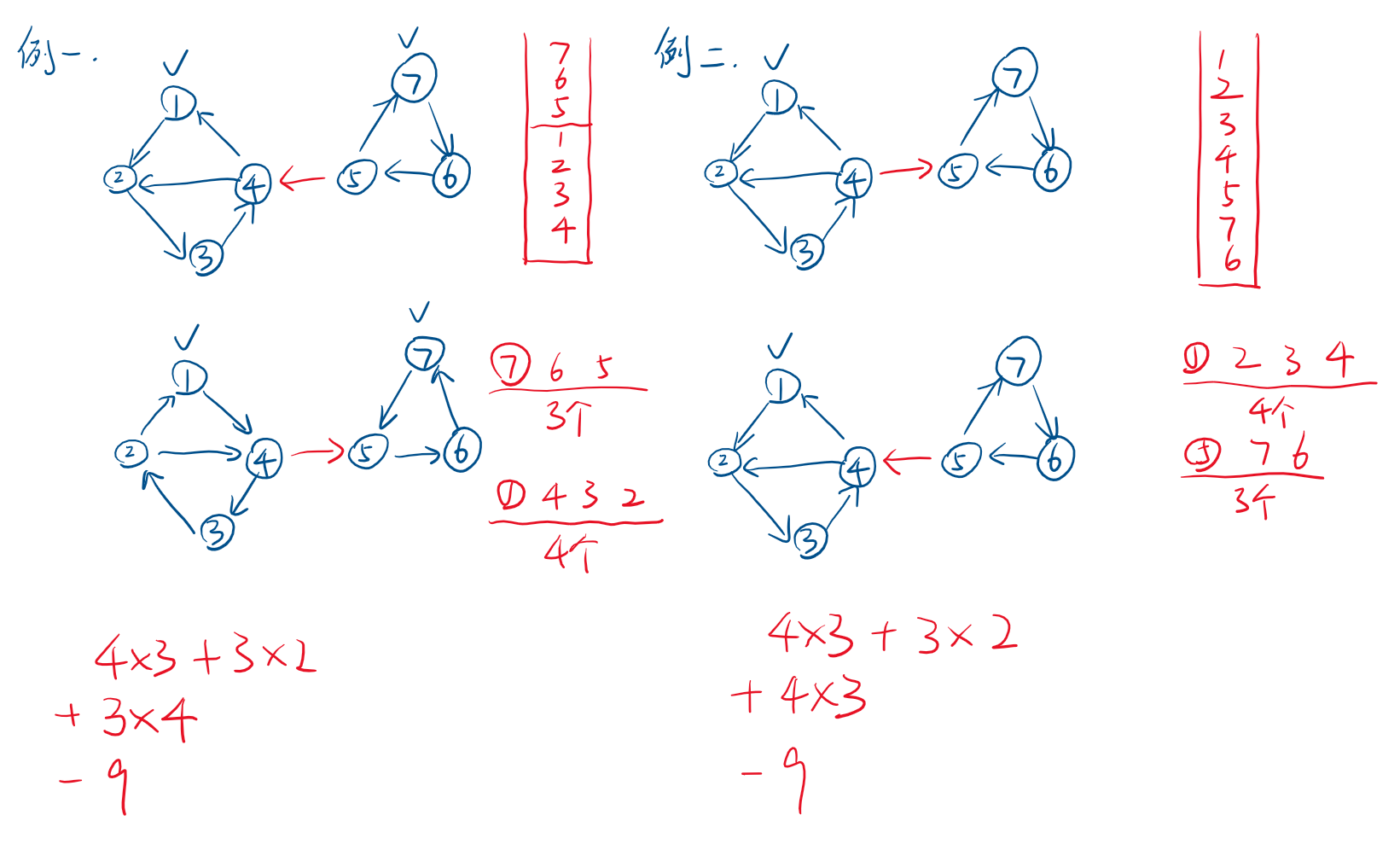
所以先将图分解为多个强连通分量，然后将强连通分量与强连通分量之间进行拓扑排序，假设拓扑排序后各个强连通分量的结点数量分别为 \(n_1, n_2, ... , n_k\)，则强连通分量之间需要增加的边数为 $n_1 \times n_2 \times ... \times n_k + n_2 \times n_3 \times ... \times n_k + ... + n_{k - 1} \times n_k - $ 强连通分量之间的所有边数。

可以用 \(Tarjan\) 算法加拓扑排序，也可以直接用两遍 \(DFS\)。

对原图跑一遍 \(DFS\)，再对反向图跑一遍 \(DFS\)。由于把强连通分量的所有边反向后还是强连通分量，而强连通分量之间的边反向后 \(DFS\) 就不可达了。第一遍 \(DFS\) 用栈记录访问顺序，第二遍根据出栈顺序 \(DFS\)，这样就可以找出所有强连通分量了，顺便还找到拓扑序了，具体见图和代码。

#include <bits/stdc++.h>
using namespace std;

vector<int> g[3000], gg[3000];

int vis1[3000], vis[3000];

stack<int> st;

void dfs(int s) {
    vis[s] = 1;
    for(int i = 0; i < g[s].size(); ++i) {
        int to = g[s][i];
        if(!vis[to]) {
            dfs(to);
        }
    }
    st.push(s);
}

int dfs1(int s) {
    vis1[s] = 1;
    int res = 1;
    for(int i = 0; i < gg[s].size(); ++i) {
        int to = gg[s][i];
        if(!vis1[to]) {
            res += dfs1(to);
        }
    }
    return res;
}

int main() {
    int n;
    scanf("%d", &n);
    int cnt = 0;
    for(int i = 1; i <= n; ++i) {
        for(int j = 1; j <= n; ++j) {
            int a;
            scanf("%d", &a);
            if(a) {
                g[i].push_back(j);
                gg[j].push_back(i);
                cnt++;
            }
        }
    }

    for(int i = 1; i <= n; ++i) {
        if(!vis[i]) {
            dfs(i);
        }
    }

    vector<int> vt;

    for(int i = 1; i <= n; ++i) {
        int h = st.top();
        st.pop();
        if(!vis1[h]) {
            vt.push_back(dfs1(h));
        }
    }

    int ans = 0;
    for(int i = 0; i < vt.size(); ++i) {
        ans += vt[i] * (vt[i] - 1);
        for(int j = i + 1; j < vt.size(); ++j) {
            ans += vt[i] * vt[j];
        }
    }
    printf("%d\n", ans - cnt);
    return 0;
}