[CSP-S模拟测试]:array（单调栈）

题目描述

　　在放完棋子之后，$dirty$又开始了新的游戏。
　　现在他拥有一个长为$n$的数组$A$，他定义第$i$个位置的分值为$i−k+1$，其中$k$需要满足：
　　对于任意满足$k\leqslant j\leqslant i$的$j$，有$A[k]\leqslant A[j]\leqslant A[i]$。当对于第$i$个数，有多个$k$满足条件时，取能获得较大分值的$k$。
　　现在，$dirty$想要知道$A$数组中分值最大的位置对应的分值为多少。

---

输入格式

第一行一个整数$n$，表示$A$数组的长度。
第二行$n$个整数，第$i$个数表示$A[i]$的值。

---

输出格式

输出一行一个整数，表示$A$数组中分值最大的位置对应的分值。

---

样例

样例输入：

8
8 6 1 7 9 2 3 8

样例输出：

3

---

数据范围与提示

注意由于$n$的范围较大，本题可能需要使用更快的读入方法。

对于$10\%$的数据，$n\leqslant 10^3$；
对于$40\%$的数据，$n\leqslant 3\times 10^5$；
对于另外$20\%$的数据为随机数据，且$n\leqslant 10^6$；
对于$100\%$的数据，$1\leqslant n\leqslant 10^7$；$1\leqslant A[i]\leqslant 10^9$。

---

题解

先来解释一下题意，对于区间$[k,i]$，我们只用保证中间的所有元素都大于等于$A[k]$，比小于等于$A[i]$即可，而不用关注其内部大小关系。

分值越大意味着$k$越小。

接下来说一下我考场上的思路，发现对于每一个$i$其最小的$k$位于其前面最后一个比它大的数之间最小的数，也就是如下图$\downarrow$

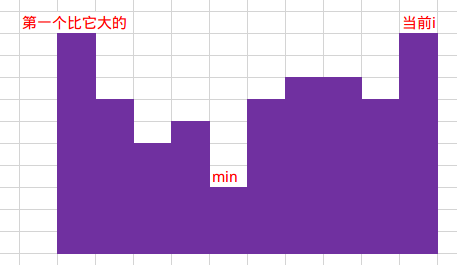
那么我们可以用单调栈维护第一个比它大的，然后用线段树查询区间最小值的位置即可，然后它就$\downarrow$

这个思路最傻的地方在于为何不用单调栈在维护一个最小值……

时间复杂度：$\Theta(n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

$60\%$算法：

#include<bits/stdc++.h>
#define int int_least32_t
#define L(x) x<<1
#define R(x) x<<1|1
using namespace std;
const int L=1<<20|1;
char buffer[L],*S,*T;
#define inline  __attribute__((optimize("-O3")))
#define getchar() ((S==T&&(T=(S=buffer)+fread(buffer,1,L,stdin),S==T))?EOF:*S++)
int n;
int a[10000010];
int ans;
int trmin[40000010],pmin[40000010];
int sta[10000010],top;
inline int read(){
	int ss(0);char bb(getchar());
	while(bb<48||bb>57)bb=getchar();
	while(bb>=48&&bb<=57)ss=(ss<<1)+(ss<<3)+(bb^48),bb=getchar();
	return ss;
}
inline void pushup(int x)
{
	if(trmin[L(x)]<=trmin[R(x)])
	{
		trmin[x]=trmin[L(x)];
		pmin[x]=pmin[L(x)];
	}
	else
	{
		trmin[x]=trmin[R(x)];
		pmin[x]=pmin[R(x)];
	}
}
inline void build(int x,int l,int r)
{
	if(l==r){trmin[x]=a[l];pmin[x]=l;return;}
	int mid=(l+r)>>1;
	build(L(x),l,mid);
	build(R(x),mid+1,r);
	pushup(x);
}
inline pair<int,int> askmin(int x,int l,int r,int L,int R)
{
	if(r<L||R<l)return make_pair(-0x3f3f3f3f,0x3f3f3f3f);
	if(L<=l&&r<=R)return make_pair(pmin[x],trmin[x]);
	int mid=(l+r)>>1;
	pair<int,int> lft=askmin(L(x),l,mid,L,R);
	pair<int,int> rht=askmin(R(x),mid+1,r,L,R);
	return lft.second<=rht.second?lft:rht;
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++)a[i]=read();
	a[n+1]=0x3f3f3f3f;
	build(1,1,n+1);
	for(int i=1;i<=n;i++)
	{
		while(top&&a[sta[top]]<=a[i])top--;
		int flag=sta[top]+1;
		sta[++top]=i;
		if(i-flag<ans)continue;
		pair<int,int> minn=askmin(1,1,n+1,flag,i);
		ans=max(ans,i-minn.first+1);
	}
	printf("%d",ans);
	return 0;
}

$100\%$算法：

#include<bits/stdc++.h>
using namespace std;
int n;
int a[10000001],sta[10000001],maxn[10000001];
int ans;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	for(int i=1;i<=n;i++)
	{
		while(sta[0]&&a[i]<a[sta[sta[0]]])
		{
			if(a[maxn[sta[0]-1]]<=a[maxn[sta[0]]])maxn[sta[0]-1]=maxn[sta[0]];
			ans=max(ans,maxn[sta[0]]-sta[sta[0]]+1);
			maxn[sta[0]--]=0;
		}
		sta[++sta[0]]=i;
		maxn[sta[0]]=i;
	}
	while(sta[0])
	{
		if(a[maxn[sta[0]-1]]<=a[maxn[sta[0]]])maxn[sta[0]-1]=maxn[sta[0]];
		ans=max(ans,maxn[sta[0]]-sta[sta[0]]+1);
		maxn[sta[0]--]=0;
	}
	printf("%d",ans);
	return 0;
}

---

rp++